Cross-Task Linearity Emerges in the Pretraining-Finetuning Paradigm

The pretraining-finetuning paradigm has become the prevailing trend in modern deep learning. In this work, we discover an intriguing linear phenomenon in models that are initialized from a common pretrained checkpoint and finetuned on different tasks, termed as Cross-Task Linearity (CTL). Specifically, if we linearly interpolate the weights of two finetuned models, the features in the weight-interpolated model are approximately equal to the linear interpolation of features in two finetuned models at each layer. Such cross-task linearity has not been noted in peer literature. We provide comprehensive empirical evidence supporting that CTL consistently occurs for finetuned models that start from the same pretrained checkpoint. We conjecture that in the pretraining-finetuning paradigm, neural networks essentially function as linear maps, mapping from the parameter space to the feature space. Based on this viewpoint, our study unveils novel insights into explaining model merging/editing, particularly by translating operations from the parameter space to the feature space. Furthermore, we delve deeper into the underlying factors for the emergence of CTL, emphasizing the impact of pretraining.

The Importance of Prompt Tuning for Automated Neuron Explanations

Recent advances have greatly increased the capabilities of large language models (LLMs), but our understanding of the models and their safety has not progressed as fast. In this paper we aim to understand LLMs deeper by studying their individual neurons. We build upon previous work showing large language models such as GPT-4 can be useful in explaining what each neuron in a language model does. Specifically, we analyze the effect of the prompt used to generate explanations and show that reformatting the explanation prompt in a more natural way can significantly improve neuron explanation quality and greatly reduce computational cost. We demonstrate the effects of our new prompts in three different ways, incorporating both automated and human evaluations.

Quantifying the Knowledge in a DNN to Explain Knowledge Distillation for Classification

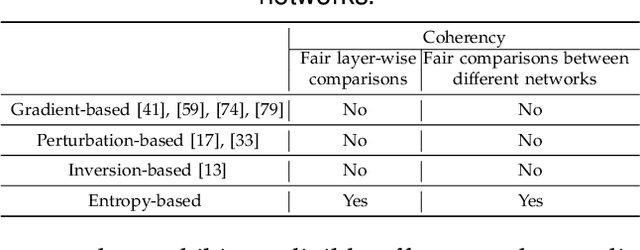
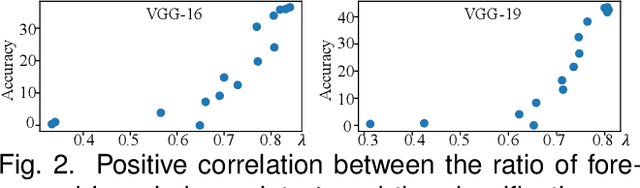
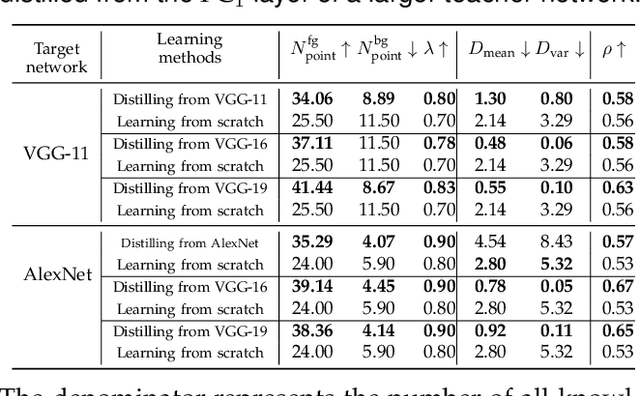
Compared to traditional learning from scratch, knowledge distillation sometimes makes the DNN achieve superior performance. This paper provides a new perspective to explain the success of knowledge distillation, i.e., quantifying knowledge points encoded in intermediate layers of a DNN for classification, based on the information theory. To this end, we consider the signal processing in a DNN as the layer-wise information discarding. A knowledge point is referred to as an input unit, whose information is much less discarded than other input units. Thus, we propose three hypotheses for knowledge distillation based on the quantification of knowledge points. 1. The DNN learning from knowledge distillation encodes more knowledge points than the DNN learning from scratch. 2. Knowledge distillation makes the DNN more likely to learn different knowledge points simultaneously. In comparison, the DNN learning from scratch tends to encode various knowledge points sequentially. 3. The DNN learning from knowledge distillation is often optimized more stably than the DNN learning from scratch. In order to verify the above hypotheses, we design three types of metrics with annotations of foreground objects to analyze feature representations of the DNN, \textit{i.e.} the quantity and the quality of knowledge points, the learning speed of different knowledge points, and the stability of optimization directions. In experiments, we diagnosed various DNNs for different classification tasks, i.e., image classification, 3D point cloud classification, binary sentiment classification, and question answering, which verified above hypotheses.

Demystify Optimization and Generalization of Over-parameterized PAC-Bayesian Learning

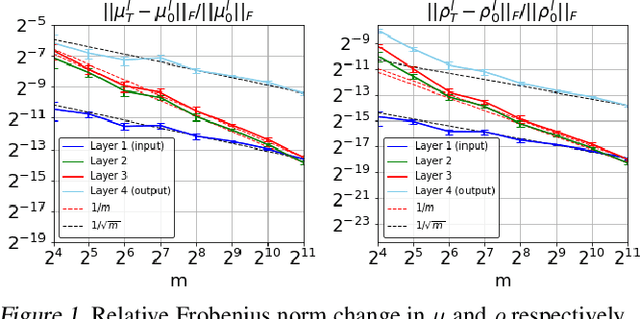
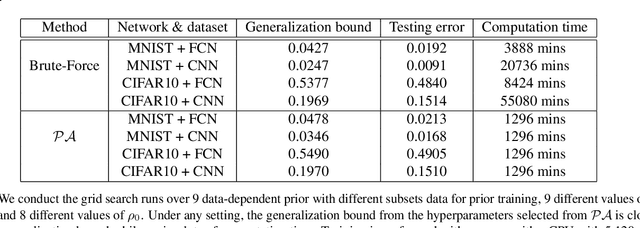
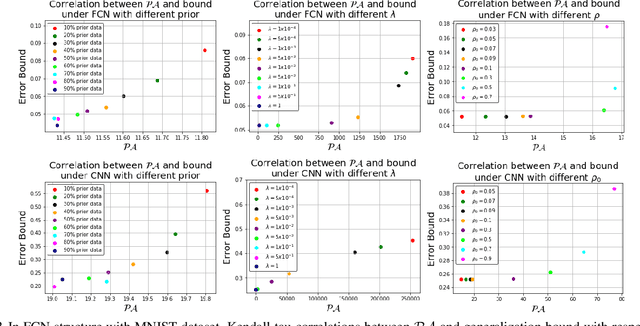
PAC-Bayesian is an analysis framework where the training error can be expressed as the weighted average of the hypotheses in the posterior distribution whilst incorporating the prior knowledge. In addition to being a pure generalization bound analysis tool, PAC-Bayesian bound can also be incorporated into an objective function to train a probabilistic neural network, making them a powerful and relevant framework that can numerically provide a tight generalization bound for supervised learning. For simplicity, we call probabilistic neural network learned using training objectives derived from PAC-Bayesian bounds as {\it PAC-Bayesian learning}. Despite their empirical success, the theoretical analysis of PAC-Bayesian learning for neural networks is rarely explored. This paper proposes a new class of convergence and generalization analysis for PAC-Bayes learning when it is used to train the over-parameterized neural networks by the gradient descent method. For a wide probabilistic neural network, we show that when PAC-Bayes learning is applied, the convergence result corresponds to solving a kernel ridge regression when the probabilistic neural tangent kernel (PNTK) is used as its kernel. Based on this finding, we further characterize the uniform PAC-Bayesian generalization bound which improves over the Rademacher complexity-based bound for non-probabilistic neural network. Finally, drawing the insight from our theoretical results, we propose a proxy measure for efficient hyperparameters selection, which is proven to be time-saving.

On the Equivalence between Neural Network and Support Vector Machine

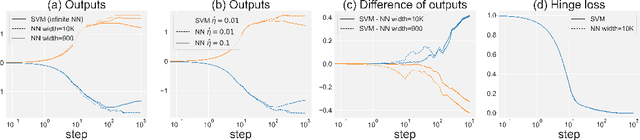
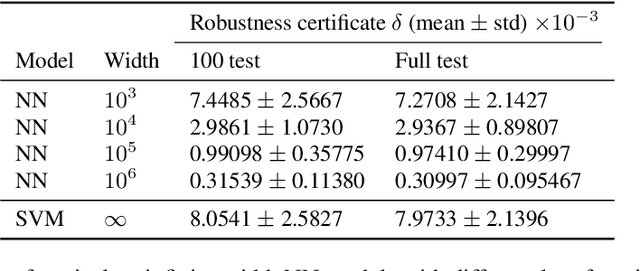
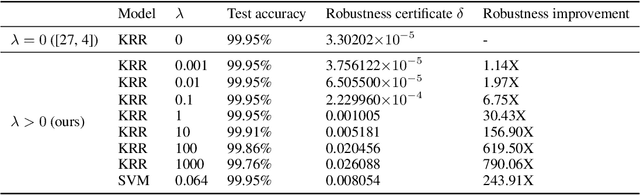
Recent research shows that the dynamics of an infinitely wide neural network (NN) trained by gradient descent can be characterized by Neural Tangent Kernel (NTK) \citep{jacot2018neural}. Under the squared loss, the infinite-width NN trained by gradient descent with an infinitely small learning rate is equivalent to kernel regression with NTK \citep{arora2019exact}. However, the equivalence is only known for ridge regression currently \citep{arora2019harnessing}, while the equivalence between NN and other kernel machines (KMs), e.g. support vector machine (SVM), remains unknown. Therefore, in this work, we propose to establish the equivalence between NN and SVM, and specifically, the infinitely wide NN trained by soft margin loss and the standard soft margin SVM with NTK trained by subgradient descent. Our main theoretical results include establishing the equivalence between NN and a broad family of $\ell_2$ regularized KMs with finite-width bounds, which cannot be handled by prior work, and showing that every finite-width NN trained by such regularized loss functions is approximately a KM. Furthermore, we demonstrate our theory can enable three practical applications, including (i) \textit{non-vacuous} generalization bound of NN via the corresponding KM; (ii) \textit{non-trivial} robustness certificate for the infinite-width NN (while existing robustness verification methods would provide vacuous bounds); (iii) intrinsically more robust infinite-width NNs than those from previous kernel regression. Our code for the experiments are available at \url{https://github.com/leslie-CH/equiv-nn-svm}.

Explaining Knowledge Distillation by Quantifying the Knowledge

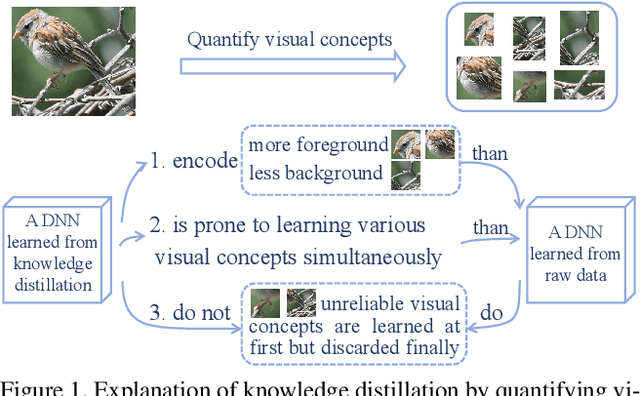
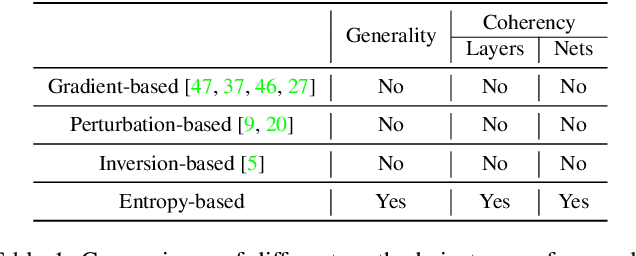
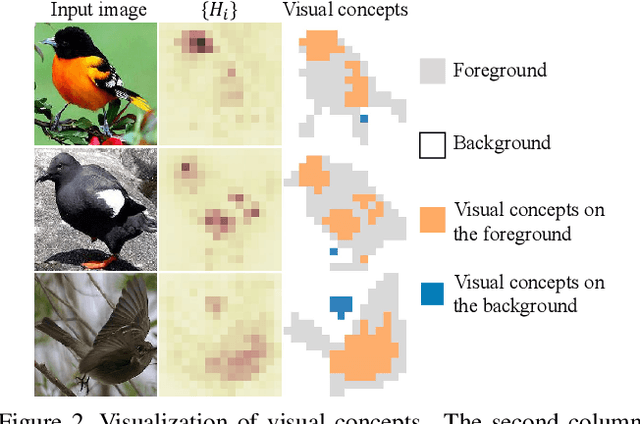
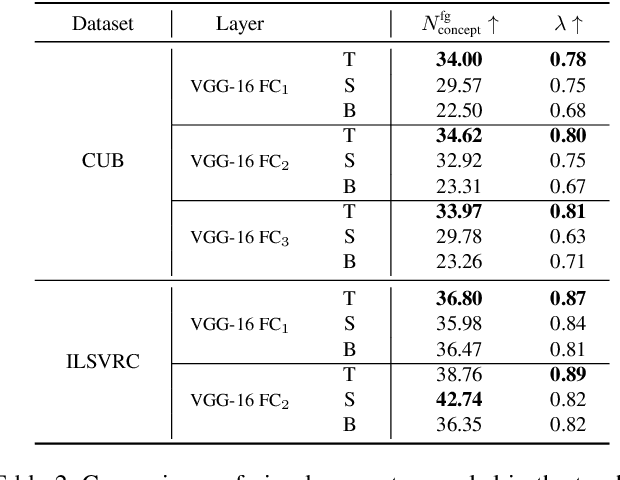
This paper presents a method to interpret the success of knowledge distillation by quantifying and analyzing task-relevant and task-irrelevant visual concepts that are encoded in intermediate layers of a deep neural network (DNN). More specifically, three hypotheses are proposed as follows. 1. Knowledge distillation makes the DNN learn more visual concepts than learning from raw data. 2. Knowledge distillation ensures that the DNN is prone to learning various visual concepts simultaneously. Whereas, in the scenario of learning from raw data, the DNN learns visual concepts sequentially. 3. Knowledge distillation yields more stable optimization directions than learning from raw data. Accordingly, we design three types of mathematical metrics to evaluate feature representations of the DNN. In experiments, we diagnosed various DNNs, and above hypotheses were verified.