Demystify Optimization and Generalization of Over-parameterized PAC-Bayesian Learning

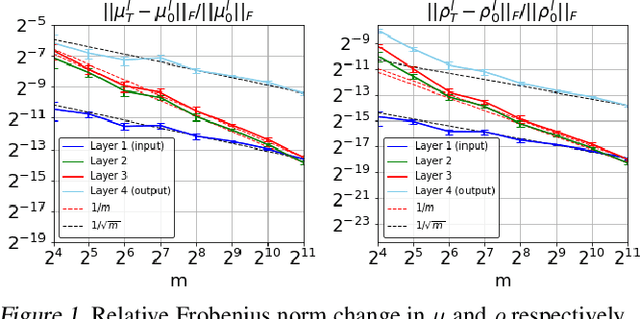
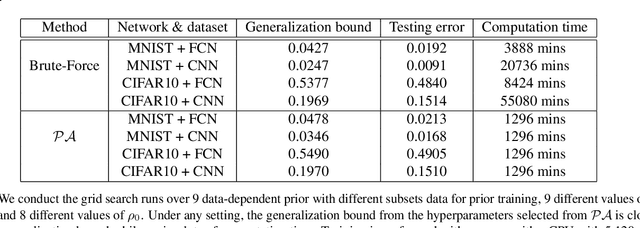
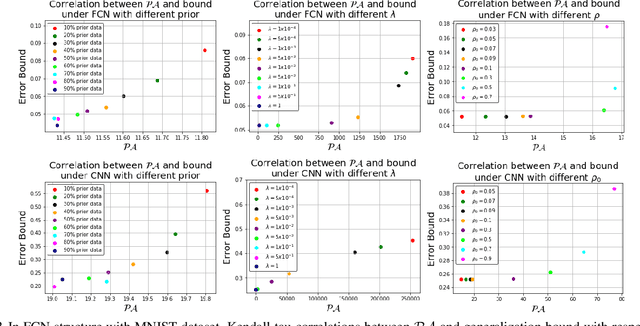
PAC-Bayesian is an analysis framework where the training error can be expressed as the weighted average of the hypotheses in the posterior distribution whilst incorporating the prior knowledge. In addition to being a pure generalization bound analysis tool, PAC-Bayesian bound can also be incorporated into an objective function to train a probabilistic neural network, making them a powerful and relevant framework that can numerically provide a tight generalization bound for supervised learning. For simplicity, we call probabilistic neural network learned using training objectives derived from PAC-Bayesian bounds as {\it PAC-Bayesian learning}. Despite their empirical success, the theoretical analysis of PAC-Bayesian learning for neural networks is rarely explored. This paper proposes a new class of convergence and generalization analysis for PAC-Bayes learning when it is used to train the over-parameterized neural networks by the gradient descent method. For a wide probabilistic neural network, we show that when PAC-Bayes learning is applied, the convergence result corresponds to solving a kernel ridge regression when the probabilistic neural tangent kernel (PNTK) is used as its kernel. Based on this finding, we further characterize the uniform PAC-Bayesian generalization bound which improves over the Rademacher complexity-based bound for non-probabilistic neural network. Finally, drawing the insight from our theoretical results, we propose a proxy measure for efficient hyperparameters selection, which is proven to be time-saving.

Implicit bias of deep linear networks in the large learning rate phase

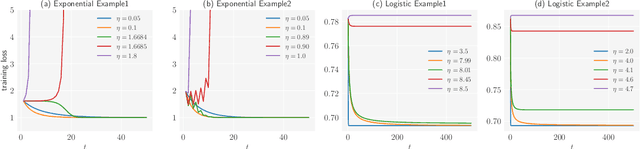
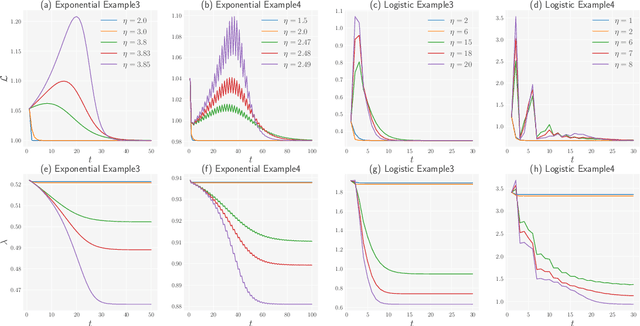
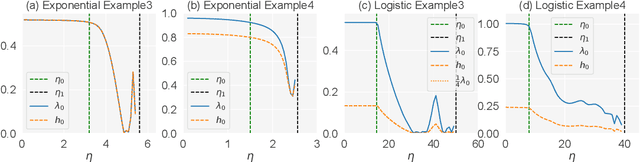
Most theoretical studies explaining the regularization effect in deep learning have only focused on gradient descent with a sufficient small learning rate or even gradient flow (infinitesimal learning rate). Such researches, however, have neglected a reasonably large learning rate applied in most practical applications. In this work, we characterize the implicit bias effect of deep linear networks for binary classification using the logistic loss in the large learning rate regime, inspired by the seminal work by Lewkowycz et al. [26] in a regression setting with squared loss. They found a learning rate regime with a large stepsize named the catapult phase, where the loss grows at the early stage of training and eventually converges to a minimum that is flatter than those found in the small learning rate regime. We claim that depending on the separation conditions of data, the gradient descent iterates will converge to a flatter minimum in the catapult phase. We rigorously prove this claim under the assumption of degenerate data by overcoming the difficulty of the non-constant Hessian of logistic loss and further characterize the behavior of loss and Hessian for non-separable data. Finally, we demonstrate that flatter minima in the space spanned by non-separable data along with the learning rate in the catapult phase can lead to better generalization empirically.