Demystify Optimization and Generalization of Over-parameterized PAC-Bayesian Learning
Paper and Code
Feb 04, 2022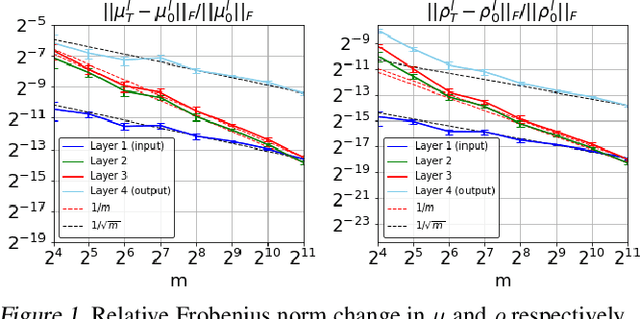
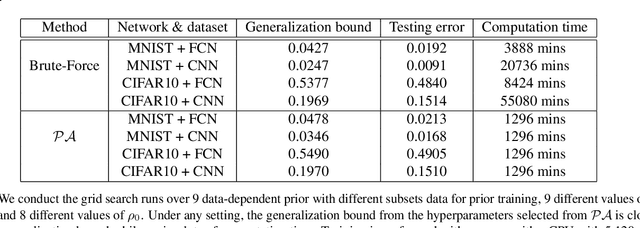
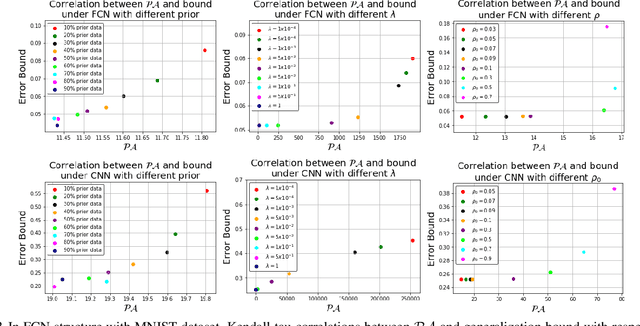
PAC-Bayesian is an analysis framework where the training error can be expressed as the weighted average of the hypotheses in the posterior distribution whilst incorporating the prior knowledge. In addition to being a pure generalization bound analysis tool, PAC-Bayesian bound can also be incorporated into an objective function to train a probabilistic neural network, making them a powerful and relevant framework that can numerically provide a tight generalization bound for supervised learning. For simplicity, we call probabilistic neural network learned using training objectives derived from PAC-Bayesian bounds as {\it PAC-Bayesian learning}. Despite their empirical success, the theoretical analysis of PAC-Bayesian learning for neural networks is rarely explored. This paper proposes a new class of convergence and generalization analysis for PAC-Bayes learning when it is used to train the over-parameterized neural networks by the gradient descent method. For a wide probabilistic neural network, we show that when PAC-Bayes learning is applied, the convergence result corresponds to solving a kernel ridge regression when the probabilistic neural tangent kernel (PNTK) is used as its kernel. Based on this finding, we further characterize the uniform PAC-Bayesian generalization bound which improves over the Rademacher complexity-based bound for non-probabilistic neural network. Finally, drawing the insight from our theoretical results, we propose a proxy measure for efficient hyperparameters selection, which is proven to be time-saving.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge