Quanshi Zhang
The Interaction Bottleneck of Deep Neural Networks: Discovery, Proof, and Modulation
Dec 21, 2025Abstract:Understanding what kinds of cooperative structures deep neural networks (DNNs) can represent remains a fundamental yet insufficiently understood problem. In this work, we treat interactions as the fundamental units of such structure and investigate a largely unexplored question: how DNNs encode interactions under different levels of contextual complexity, and how these microscopic interaction patterns shape macroscopic representation capacity. To quantify this complexity, we use multi-order interactions [57], where each order reflects the amount of contextual information required to evaluate the joint interaction utility of a variable pair. This formulation enables a stratified analysis of cooperative patterns learned by DNNs. Building on this formulation, we develop a comprehensive study of interaction structure in DNNs. (i) We empirically discover a universal interaction bottleneck: across architectures and tasks, DNNs easily learn low-order and high-order interactions but consistently under-represent mid-order ones. (ii) We theoretically explain this bottleneck by proving that mid-order interactions incur the highest contextual variability, yielding large gradient variance and making them intrinsically difficult to learn. (iii) We further modulate the bottleneck by introducing losses that steer models toward emphasizing interactions of selected orders. Finally, we connect microscopic interaction structures with macroscopic representational behavior: low-order-emphasized models exhibit stronger generalization and robustness, whereas high-order-emphasized models demonstrate greater structural modeling and fitting capability. Together, these results uncover an inherent representational bias in modern DNNs and establish interaction order as a powerful lens for interpreting and guiding deep representations.
Attribution Explanations for Deep Neural Networks: A Theoretical Perspective
Aug 11, 2025Abstract:Attribution explanation is a typical approach for explaining deep neural networks (DNNs), inferring an importance or contribution score for each input variable to the final output. In recent years, numerous attribution methods have been developed to explain DNNs. However, a persistent concern remains unresolved, i.e., whether and which attribution methods faithfully reflect the actual contribution of input variables to the decision-making process. The faithfulness issue undermines the reliability and practical utility of attribution explanations. We argue that these concerns stem from three core challenges. First, difficulties arise in comparing attribution methods due to their unstructured heterogeneity, differences in heuristics, formulations, and implementations that lack a unified organization. Second, most methods lack solid theoretical underpinnings, with their rationales remaining absent, ambiguous, or unverified. Third, empirically evaluating faithfulness is challenging without ground truth. Recent theoretical advances provide a promising way to tackle these challenges, attracting increasing attention. We summarize these developments, with emphasis on three key directions: (i) Theoretical unification, which uncovers commonalities and differences among methods, enabling systematic comparisons; (ii) Theoretical rationale, clarifying the foundations of existing methods; (iii) Theoretical evaluation, rigorously proving whether methods satisfy faithfulness principles. Beyond a comprehensive review, we provide insights into how these studies help deepen theoretical understanding, inform method selection, and inspire new attribution methods. We conclude with a discussion of promising open problems for further work.
Towards the Three-Phase Dynamics of Generalization Power of a DNN
May 11, 2025Abstract:This paper proposes a new perspective for analyzing the generalization power of deep neural networks (DNNs), i.e., directly disentangling and analyzing the dynamics of generalizable and non-generalizable interaction encoded by a DNN through the training process. Specifically, this work builds upon the recent theoretical achievement in explainble AI, which proves that the detailed inference logic of DNNs can be can be strictly rewritten as a small number of AND-OR interaction patterns. Based on this, we propose an efficient method to quantify the generalization power of each interaction, and we discover a distinct three-phase dynamics of the generalization power of interactions during training. In particular, the early phase of training typically removes noisy and non-generalizable interactions and learns simple and generalizable ones. The second and the third phases tend to capture increasingly complex interactions that are harder to generalize. Experimental results verify that the learning of non-generalizable interactions is the the direct cause for the gap between the training and testing losses.
Towards the Resistance of Neural Network Watermarking to Fine-tuning
May 02, 2025
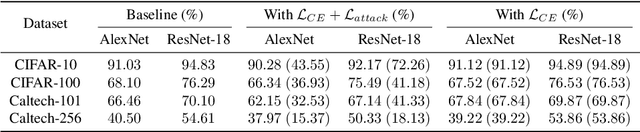


Abstract:This paper proves a new watermarking method to embed the ownership information into a deep neural network (DNN), which is robust to fine-tuning. Specifically, we prove that when the input feature of a convolutional layer only contains low-frequency components, specific frequency components of the convolutional filter will not be changed by gradient descent during the fine-tuning process, where we propose a revised Fourier transform to extract frequency components from the convolutional filter. Additionally, we also prove that these frequency components are equivariant to weight scaling and weight permutations. In this way, we design a watermark module to encode the watermark information to specific frequency components in a convolutional filter. Preliminary experiments demonstrate the effectiveness of our method.
Randomness of Low-Layer Parameters Determines Confusing Samples in Terms of Interaction Representations of a DNN
Feb 12, 2025Abstract:In this paper, we find that the complexity of interactions encoded by a deep neural network (DNN) can explain its generalization power. We also discover that the confusing samples of a DNN, which are represented by non-generalizable interactions, are determined by its low-layer parameters. In comparison, other factors, such as high-layer parameters and network architecture, have much less impact on the composition of confusing samples. Two DNNs with different low-layer parameters usually have fully different sets of confusing samples, even though they have similar performance. This finding extends the understanding of the lottery ticket hypothesis, and well explains distinctive representation power of different DNNs.
Disentangling Regional Primitives for Image Generation
Oct 06, 2024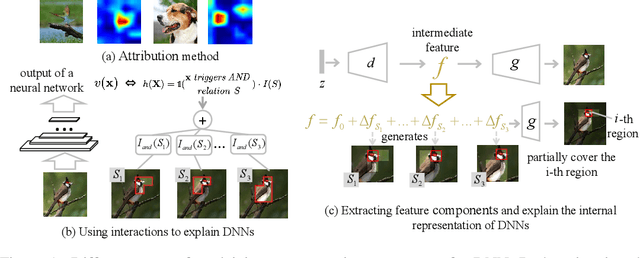
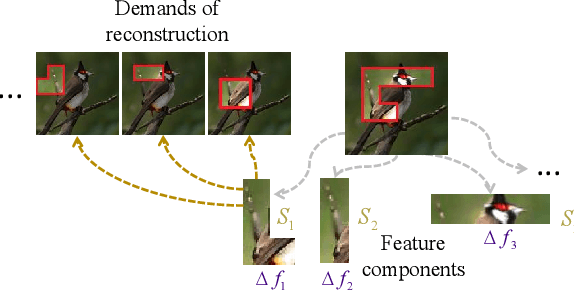


Abstract:This paper presents a method to explain the internal representation structure of a neural network for image generation. Specifically, our method disentangles primitive feature components from the intermediate-layer feature of the neural network, which ensures that each feature component is exclusively used to generate a specific set of image regions. In this way, the generation of the entire image can be considered as the superposition of different pre-encoded primitive regional patterns, each being generated by a feature component. We find that the feature component can be represented as an OR relationship between the demands for generating different image regions, which is encoded by the neural network. Therefore, we extend the Harsanyi interaction to represent such an OR interaction to disentangle the feature component. Experiments show a clear correspondence between each feature component and the generation of specific image regions.
Alignment Between the Decision-Making Logic of LLMs and Human Cognition: A Case Study on Legal LLMs
Oct 06, 2024



Abstract:This paper presents a method to evaluate the alignment between the decision-making logic of Large Language Models (LLMs) and human cognition in a case study on legal LLMs. Unlike traditional evaluations on language generation results, we propose to evaluate the correctness of the detailed decision-making logic of an LLM behind its seemingly correct outputs, which represents the core challenge for an LLM to earn human trust. To this end, we quantify the interactions encoded by the LLM as primitive decision-making logic, because recent theoretical achievements have proven several mathematical guarantees of the faithfulness of the interaction-based explanation. We design a set of metrics to evaluate the detailed decision-making logic of LLMs. Experiments show that even when the language generation results appear correct, a significant portion of the internal inference logic contains notable issues.
Layerwise Change of Knowledge in Neural Networks
Sep 13, 2024



Abstract:This paper aims to explain how a deep neural network (DNN) gradually extracts new knowledge and forgets noisy features through layers in forward propagation. Up to now, although the definition of knowledge encoded by the DNN has not reached a consensus, Previous studies have derived a series of mathematical evidence to take interactions as symbolic primitive inference patterns encoded by a DNN. We extend the definition of interactions and, for the first time, extract interactions encoded by intermediate layers. We quantify and track the newly emerged interactions and the forgotten interactions in each layer during the forward propagation, which shed new light on the learning behavior of DNNs. The layer-wise change of interactions also reveals the change of the generalization capacity and instability of feature representations of a DNN.
Towards the Dynamics of a DNN Learning Symbolic Interactions
Jul 27, 2024Abstract:This study proves the two-phase dynamics of a deep neural network (DNN) learning interactions. Despite the long disappointing view of the faithfulness of post-hoc explanation of a DNN, in recent years, a series of theorems have been proven to show that given an input sample, a small number of interactions between input variables can be considered as primitive inference patterns, which can faithfully represent every detailed inference logic of the DNN on this sample. Particularly, it has been observed that various DNNs all learn interactions of different complexities with two-phase dynamics, and this well explains how a DNN's generalization power changes from under-fitting to over-fitting. Therefore, in this study, we prove the dynamics of a DNN gradually encoding interactions of different complexities, which provides a theoretically grounded mechanism for the over-fitting of a DNN. Experiments show that our theory well predicts the real learning dynamics of various DNNs on different tasks.
Quantifying In-Context Reasoning Effects and Memorization Effects in LLMs
May 20, 2024



Abstract:In this study, we propose an axiomatic system to define and quantify the precise memorization and in-context reasoning effects used by the large language model (LLM) for language generation. These effects are formulated as non-linear interactions between tokens/words encoded by the LLM. Specifically, the axiomatic system enables us to categorize the memorization effects into foundational memorization effects and chaotic memorization effects, and further classify in-context reasoning effects into enhanced inference patterns, eliminated inference patterns, and reversed inference patterns. Besides, the decomposed effects satisfy the sparsity property and the universal matching property, which mathematically guarantee that the LLM's confidence score can be faithfully decomposed into the memorization effects and in-context reasoning effects. Experiments show that the clear disentanglement of memorization effects and in-context reasoning effects enables a straightforward examination of detailed inference patterns encoded by LLMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge