DecIF: Improving Instruction-Following through Meta-Decomposition

Instruction-following has emerged as a crucial capability for large language models (LLMs). However, existing approaches often rely on pre-existing documents or external resources to synthesize instruction-following data, which limits their flexibility and generalizability. In this paper, we introduce DecIF, a fully autonomous, meta-decomposition guided framework that generates diverse and high-quality instruction-following data using only LLMs. DecIF is grounded in the principle of decomposition. For instruction generation, we guide LLMs to iteratively produce various types of meta-information, which are then combined with response constraints to form well-structured and semantically rich instructions. We further utilize LLMs to detect and resolve potential inconsistencies within the generated instructions. Regarding response generation, we decompose each instruction into atomic-level evaluation criteria, enabling rigorous validation and the elimination of inaccurate instruction-response pairs. Extensive experiments across a wide range of scenarios and settings demonstrate DecIF's superior performance on instruction-following tasks. Further analysis highlights its strong flexibility, scalability, and generalizability in automatically synthesizing high-quality instruction data.

Towards the Resistance of Neural Network Watermarking to Fine-tuning

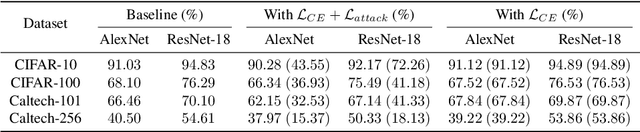
This paper proves a new watermarking method to embed the ownership information into a deep neural network (DNN), which is robust to fine-tuning. Specifically, we prove that when the input feature of a convolutional layer only contains low-frequency components, specific frequency components of the convolutional filter will not be changed by gradient descent during the fine-tuning process, where we propose a revised Fourier transform to extract frequency components from the convolutional filter. Additionally, we also prove that these frequency components are equivariant to weight scaling and weight permutations. In this way, we design a watermark module to encode the watermark information to specific frequency components in a convolutional filter. Preliminary experiments demonstrate the effectiveness of our method.

CIMFlow: An Integrated Framework for Systematic Design and Evaluation of Digital CIM Architectures

Digital Compute-in-Memory (CIM) architectures have shown great promise in Deep Neural Network (DNN) acceleration by effectively addressing the "memory wall" bottleneck. However, the development and optimization of digital CIM accelerators are hindered by the lack of comprehensive tools that encompass both software and hardware design spaces. Moreover, existing design and evaluation frameworks often lack support for the capacity constraints inherent in digital CIM architectures. In this paper, we present CIMFlow, an integrated framework that provides an out-of-the-box workflow for implementing and evaluating DNN workloads on digital CIM architectures. CIMFlow bridges the compilation and simulation infrastructures with a flexible instruction set architecture (ISA) design, and addresses the constraints of digital CIM through advanced partitioning and parallelism strategies in the compilation flow. Our evaluation demonstrates that CIMFlow enables systematic prototyping and optimization of digital CIM architectures across diverse configurations, providing researchers and designers with an accessible platform for extensive design space exploration.

Defects of Convolutional Decoder Networks in Frequency Representation

In this paper, we prove representation bottlenecks of a cascaded convolutional decoder network, considering the capacity of representing different frequency components of an input sample. We conduct the discrete Fourier transform on each channel of the feature map in an intermediate layer of the decoder network. Then, we introduce the rule of the forward propagation of such intermediate-layer spectrum maps, which is equivalent to the forward propagation of feature maps through a convolutional layer. Based on this, we find that each frequency component in the spectrum map is forward propagated independently with other frequency components. Furthermore, we prove two bottlenecks in representing feature spectrums. First, we prove that the convolution operation, the zero-padding operation, and a set of other settings all make a convolutional decoder network more likely to weaken high-frequency components. Second, we prove that the upsampling operation generates a feature spectrum, in which strong signals repetitively appears at certain frequencies.

Batch Normalization Is Blind to the First and Second Derivatives of the Loss

In this paper, we prove the effects of the BN operation on the back-propagation of the first and second derivatives of the loss. When we do the Taylor series expansion of the loss function, we prove that the BN operation will block the influence of the first-order term and most influence of the second-order term of the loss. We also find that such a problem is caused by the standardization phase of the BN operation. Experimental results have verified our theoretical conclusions, and we have found that the BN operation significantly affects feature representations in specific tasks, where losses of different samples share similar analytic formulas.