A successive difference-of-convex approximation method for a class of nonconvex nonsmooth optimization problems
Paper and Code
May 26, 2018
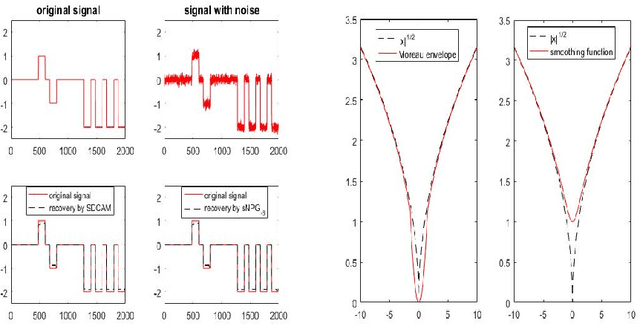
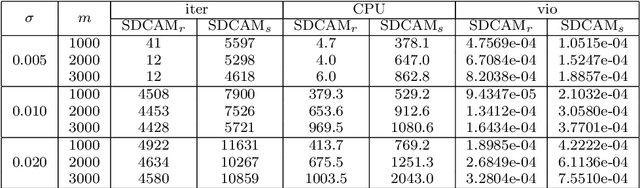
We consider a class of nonconvex nonsmooth optimization problems whose objective is the sum of a smooth function and a finite number of nonnegative proper closed possibly nonsmooth functions (whose proximal mappings are easy to compute), some of which are further composed with linear maps. This kind of problems arises naturally in various applications when different regularizers are introduced for inducing simultaneous structures in the solutions. Solving these problems, however, can be challenging because of the coupled nonsmooth functions: the corresponding proximal mapping can be hard to compute so that standard first-order methods such as the proximal gradient algorithm cannot be applied efficiently. In this paper, we propose a successive difference-of-convex approximation method for solving this kind of problems. In this algorithm, we approximate the nonsmooth functions by their Moreau envelopes in each iteration. Making use of the simple observation that Moreau envelopes of nonnegative proper closed functions are continuous {\em difference-of-convex} functions, we can then approximately minimize the approximation function by first-order methods with suitable majorization techniques. These first-order methods can be implemented efficiently thanks to the fact that the proximal mapping of {\em each} nonsmooth function is easy to compute. Under suitable assumptions, we prove that the sequence generated by our method is bounded and any accumulation point is a stationary point of the objective. We also discuss how our method can be applied to concrete applications such as nonconvex fused regularized optimization problems and simultaneously structured matrix optimization problems, and illustrate the performance numerically for these two specific applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge