Penalty methods for a class of non-Lipschitz optimization problems
Paper and Code
Apr 07, 2016

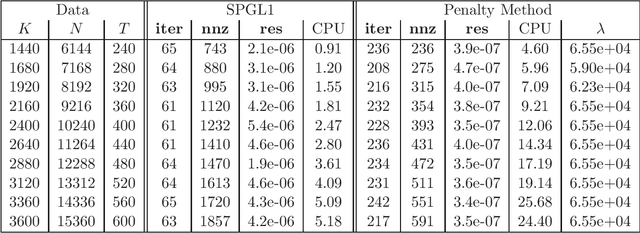
We consider a class of constrained optimization problems with a possibly nonconvex non-Lipschitz objective and a convex feasible set being the intersection of a polyhedron and a possibly degenerate ellipsoid. Such problems have a wide range of applications in data science, where the objective is used for inducing sparsity in the solutions while the constraint set models the noise tolerance and incorporates other prior information for data fitting. To solve this class of constrained optimization problems, a common approach is the penalty method. However, there is little theory on exact penalization for problems with nonconvex and non-Lipschitz objective functions. In this paper, we study the existence of exact penalty parameters regarding local minimizers, stationary points and $\epsilon$-minimizers under suitable assumptions. Moreover, we discuss a penalty method whose subproblems are solved via a nonmonotone proximal gradient method with a suitable update scheme for the penalty parameters, and prove the convergence of the algorithm to a KKT point of the constrained problem. Preliminary numerical results demonstrate the efficiency of the penalty method for finding sparse solutions of underdetermined linear systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge