Provable Optimization for Adversarial Fair Self-supervised Contrastive Learning

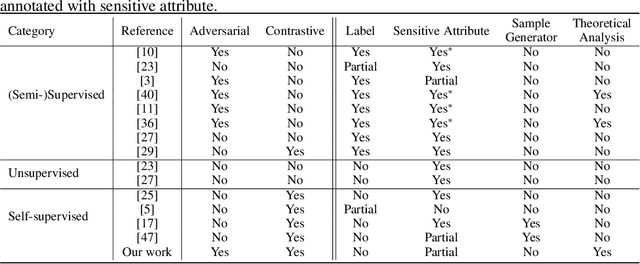
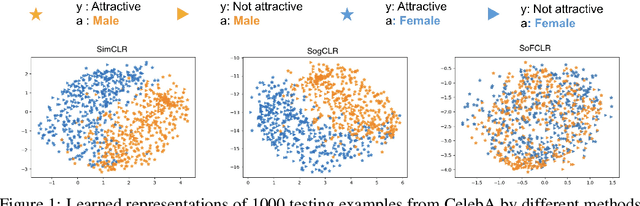
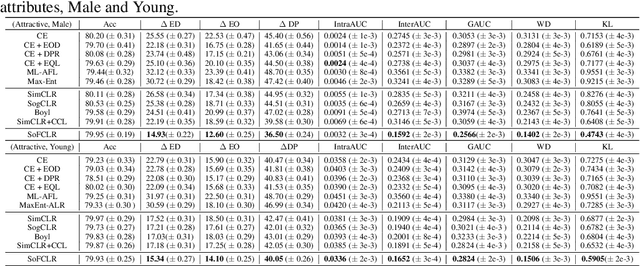
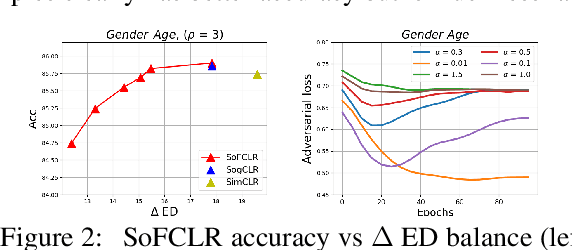
This paper studies learning fair encoders in a self-supervised learning (SSL) setting, in which all data are unlabeled and only a small portion of them are annotated with sensitive attribute. Adversarial fair representation learning is well suited for this scenario by minimizing a contrastive loss over unlabeled data while maximizing an adversarial loss of predicting the sensitive attribute over the data with sensitive attribute. Nevertheless, optimizing adversarial fair representation learning presents significant challenges due to solving a non-convex non-concave minimax game. The complexity deepens when incorporating a global contrastive loss that contrasts each anchor data point against all other examples. A central question is ``{\it can we design a provable yet efficient algorithm for solving adversarial fair self-supervised contrastive learning}?'' Building on advanced optimization techniques, we propose a stochastic algorithm dubbed SoFCLR with a convergence analysis under reasonable conditions without requring a large batch size. We conduct extensive experiments to demonstrate the effectiveness of the proposed approach for downstream classification with eight fairness notions.

Single-loop Stochastic Algorithms for Difference of Max-Structured Weakly Convex Functions

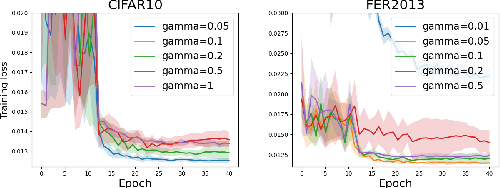
In this paper, we study a class of non-smooth non-convex problems in the form of $\min_{x}[\max_{y\in Y}\phi(x, y) - \max_{z\in Z}\psi(x, z)]$, where both $\Phi(x) = \max_{y\in Y}\phi(x, y)$ and $\Psi(x)=\max_{z\in Z}\psi(x, z)$ are weakly convex functions, and $\phi(x, y), \psi(x, z)$ are strongly concave functions in terms of $y$ and $z$, respectively. It covers two families of problems that have been studied but are missing single-loop stochastic algorithms, i.e., difference of weakly convex functions and weakly convex strongly-concave min-max problems. We propose a stochastic Moreau envelope approximate gradient method dubbed SMAG, the first single-loop algorithm for solving these problems, and provide a state-of-the-art non-asymptotic convergence rate. The key idea of the design is to compute an approximate gradient of the Moreau envelopes of $\Phi, \Psi$ using only one step of stochastic gradient update of the primal and dual variables. Empirically, we conduct experiments on positive-unlabeled (PU) learning and partial area under ROC curve (pAUC) optimization with an adversarial fairness regularizer to validate the effectiveness of our proposed algorithms.

Non-Smooth Weakly-Convex Finite-sum Coupled Compositional Optimization

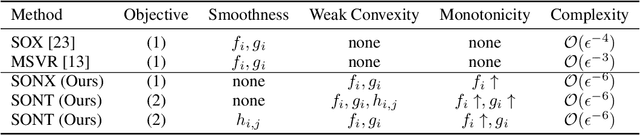
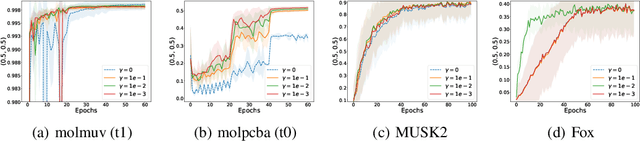
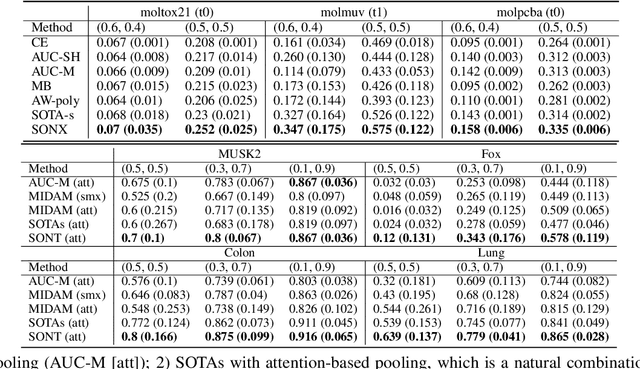
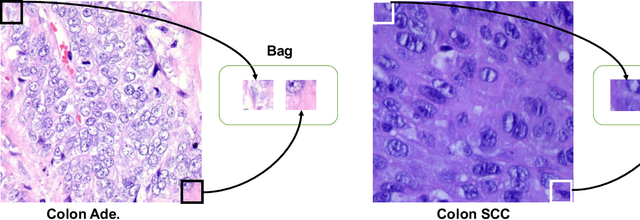
This paper investigates new families of compositional optimization problems, called $\underline{\bf n}$on-$\underline{\bf s}$mooth $\underline{\bf w}$eakly-$\underline{\bf c}$onvex $\underline{\bf f}$inite-sum $\underline{\bf c}$oupled $\underline{\bf c}$ompositional $\underline{\bf o}$ptimization (NSWC FCCO). There has been a growing interest in FCCO due to its wide-ranging applications in machine learning and AI, as well as its ability to address the shortcomings of stochastic algorithms based on empirical risk minimization. However, current research on FCCO presumes that both the inner and outer functions are smooth, limiting their potential to tackle a more diverse set of problems. Our research expands on this area by examining non-smooth weakly-convex FCCO, where the outer function is weakly convex and non-decreasing, and the inner function is weakly-convex. We analyze a single-loop algorithm and establish its complexity for finding an $\epsilon$-stationary point of the Moreau envelop of the objective function. Additionally, we also extend the algorithm to solving novel non-smooth weakly-convex tri-level finite-sum coupled compositional optimization problems, which feature a nested arrangement of three functions. Lastly, we explore the applications of our algorithms in deep learning for two-way partial AUC maximization and multi-instance two-way partial AUC maximization, using empirical studies to showcase the effectiveness of the proposed algorithms.

Blockwise Stochastic Variance-Reduced Methods with Parallel Speedup for Multi-Block Bilevel Optimization

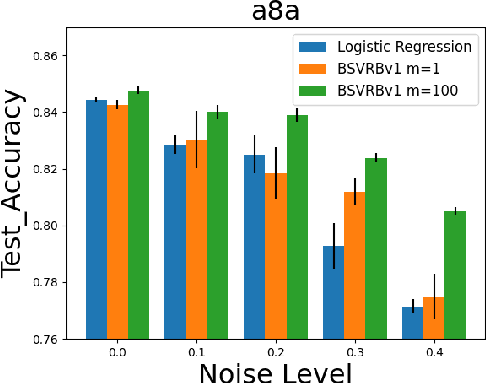
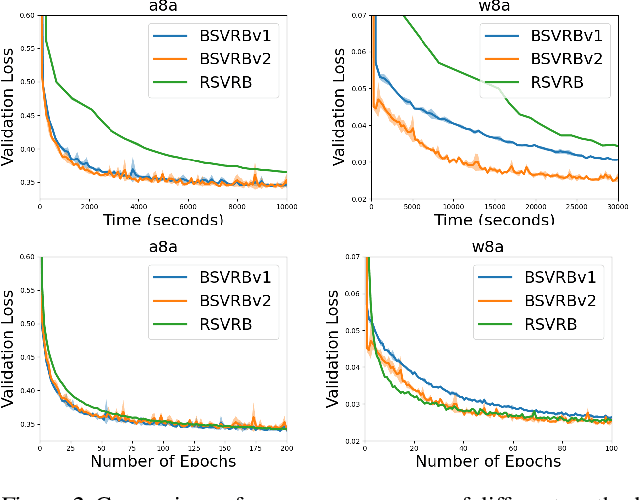
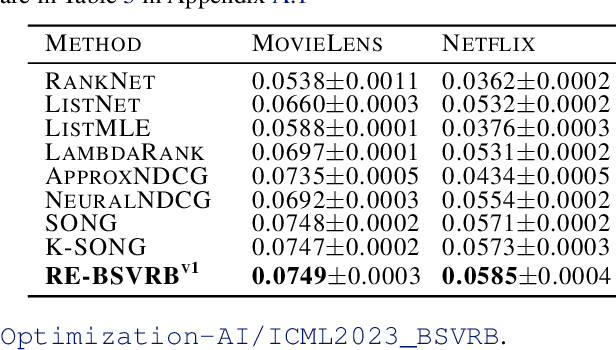
In this paper, we consider non-convex multi-block bilevel optimization (MBBO) problems, which involve $m\gg 1$ lower level problems and have important applications in machine learning. Designing a stochastic gradient and controlling its variance is more intricate due to the hierarchical sampling of blocks and data and the unique challenge of estimating hyper-gradient. We aim to achieve three nice properties for our algorithm: (a) matching the state-of-the-art complexity of standard BO problems with a single block; (b) achieving parallel speedup by sampling $I$ blocks and sampling $B$ samples for each sampled block per-iteration; (c) avoiding the computation of the inverse of a high-dimensional Hessian matrix estimator. However, it is non-trivial to achieve all of these by observing that existing works only achieve one or two of these properties. To address the involved challenges for achieving (a, b, c), we propose two stochastic algorithms by using advanced blockwise variance-reduction techniques for tracking the Hessian matrices (for low-dimensional problems) or the Hessian-vector products (for high-dimensional problems), and prove an iteration complexity of $O(\frac{m\epsilon^{-3}\mathbb{I}(I<m)}{I\sqrt{I}} + \frac{m\epsilon^{-3}}{I\sqrt{B}})$ for finding an $\epsilon$-stationary point under appropriate conditions. We also conduct experiments to verify the effectiveness of the proposed algorithms comparing with existing MBBO algorithms.

Not All Semantics are Created Equal: Contrastive Self-supervised Learning with Automatic Temperature Individualization

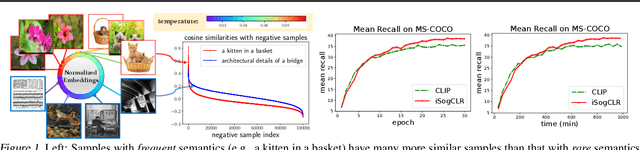
In this paper, we aim to optimize a contrastive loss with individualized temperatures in a principled and systematic manner for self-supervised learning. The common practice of using a global temperature parameter $\tau$ ignores the fact that ``not all semantics are created equal", meaning that different anchor data may have different numbers of samples with similar semantics, especially when data exhibits long-tails. First, we propose a new robust contrastive loss inspired by distributionally robust optimization (DRO), providing us an intuition about the effect of $\tau$ and a mechanism for automatic temperature individualization. Then, we propose an efficient stochastic algorithm for optimizing the robust contrastive loss with a provable convergence guarantee without using large mini-batch sizes. Theoretical and experimental results show that our algorithm automatically learns a suitable $\tau$ for each sample. Specifically, samples with frequent semantics use large temperatures to keep local semantic structures, while samples with rare semantics use small temperatures to induce more separable features. Our method not only outperforms prior strong baselines (e.g., SimCLR, CLIP) on unimodal and bimodal datasets with larger improvements on imbalanced data but also is less sensitive to hyper-parameters. To our best knowledge, this is the first methodical approach to optimizing a contrastive loss with individualized temperatures.

Multi-block Min-max Bilevel Optimization with Applications in Multi-task Deep AUC Maximization

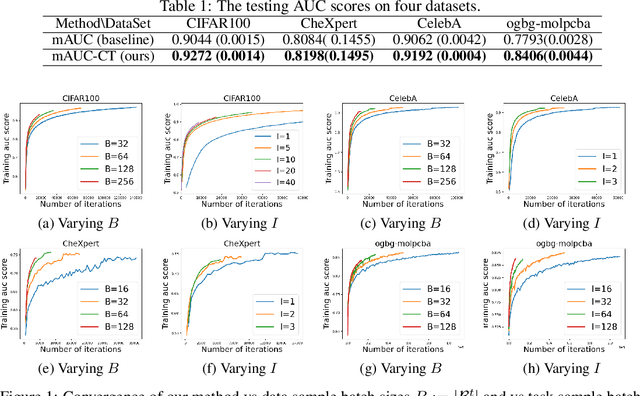
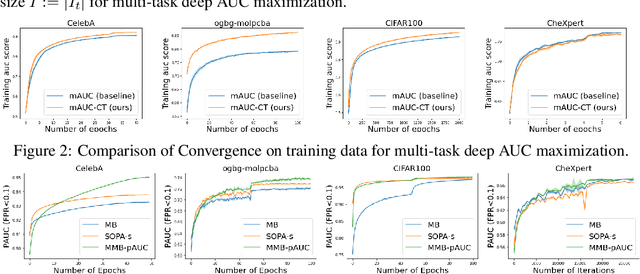
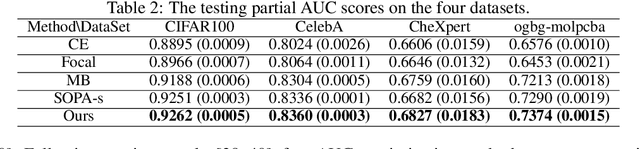
In this paper, we study multi-block min-max bilevel optimization problems, where the upper level is non-convex strongly-concave minimax objective and the lower level is a strongly convex objective, and there are multiple blocks of dual variables and lower level problems. Due to the intertwined multi-block min-max bilevel structure, the computational cost at each iteration could be prohibitively high, especially with a large number of blocks. To tackle this challenge, we present a single-loop randomized stochastic algorithm, which requires updates for only a constant number of blocks at each iteration. Under some mild assumptions on the problem, we establish its sample complexity of $\mathcal{O}(1/\epsilon^4)$ for finding an $\epsilon$-stationary point. This matches the optimal complexity for solving stochastic nonconvex optimization under a general unbiased stochastic oracle model. Moreover, we provide two applications of the proposed method in multi-task deep AUC (area under ROC curve) maximization and multi-task deep partial AUC maximization. Experimental results validate our theory and demonstrate the effectiveness of our method on problems with hundreds of tasks.

Large-scale Stochastic Optimization of NDCG Surrogates for Deep Learning with Provable Convergence

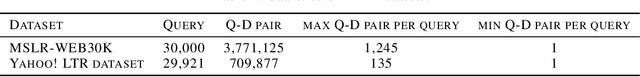
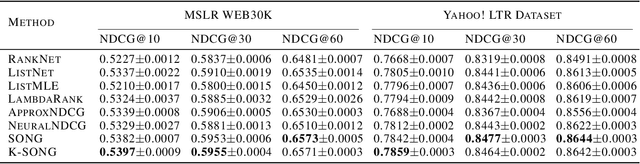
NDCG, namely Normalized Discounted Cumulative Gain, is a widely used ranking metric in information retrieval and machine learning. However, efficient and provable stochastic methods for maximizing NDCG are still lacking, especially for deep models. In this paper, we propose a principled approach to optimize NDCG and its top-$K$ variant. First, we formulate a novel compositional optimization problem for optimizing the NDCG surrogate, and a novel bilevel compositional optimization problem for optimizing the top-$K$ NDCG surrogate. Then, we develop efficient stochastic algorithms with provable convergence guarantees for the non-convex objectives. Different from existing NDCG optimization methods, the per-iteration complexity of our algorithms scales with the mini-batch size instead of the number of total items. To improve the effectiveness for deep learning, we further propose practical strategies by using initial warm-up and stop gradient operator. Experimental results on multiple datasets demonstrate that our methods outperform prior ranking approaches in terms of NDCG. To the best of our knowledge, this is the first time that stochastic algorithms are proposed to optimize NDCG with a provable convergence guarantee.