To Cool or not to Cool? Temperature Network Meets Large Foundation Models via DRO

The temperature parameter plays a profound role during training and/or inference with large foundation models (LFMs) such as large language models (LLMs) and CLIP models. Particularly, it adjusts the logits in the softmax function in LLMs, which is crucial for next token generation, and it scales the similarities in the contrastive loss for training CLIP models. A significant question remains: Is it viable to learn a neural network to predict a personalized temperature of any input data for enhancing LFMs"? In this paper, we present a principled framework for learning a small yet generalizable temperature prediction network (TempNet) to improve LFMs. Our solution is composed of a novel learning framework with a robust loss underpinned by constrained distributionally robust optimization (DRO), and a properly designed TempNet with theoretical inspiration. TempNet can be trained together with a large foundation model from scratch or learned separately given a pretrained foundation model. It is not only useful for predicting personalized temperature to promote the training of LFMs but also generalizable and transferable to new tasks. Our experiments on LLMs and CLIP models demonstrate that TempNet greatly improves the performance of existing solutions or models, e.g. Table 1. The code to reproduce the experimental results in this paper can be found at https://github.com/zhqiu/TempNet.

LibAUC: A Deep Learning Library for X-Risk Optimization

This paper introduces the award-winning deep learning (DL) library called LibAUC for implementing state-of-the-art algorithms towards optimizing a family of risk functions named X-risks. X-risks refer to a family of compositional functions in which the loss function of each data point is defined in a way that contrasts the data point with a large number of others. They have broad applications in AI for solving classical and emerging problems, including but not limited to classification for imbalanced data (CID), learning to rank (LTR), and contrastive learning of representations (CLR). The motivation of developing LibAUC is to address the convergence issues of existing libraries for solving these problems. In particular, existing libraries may not converge or require very large mini-batch sizes in order to attain good performance for these problems, due to the usage of the standard mini-batch technique in the empirical risk minimization (ERM) framework. Our library is for deep X-risk optimization (DXO) that has achieved great success in solving a variety of tasks for CID, LTR and CLR. The contributions of this paper include: (1) It introduces a new mini-batch based pipeline for implementing DXO algorithms, which differs from existing DL pipeline in the design of controlled data samplers and dynamic mini-batch losses; (2) It provides extensive benchmarking experiments for ablation studies and comparison with existing libraries. The LibAUC library features scalable performance for millions of items to be contrasted, faster and better convergence than existing libraries for optimizing X-risks, seamless PyTorch deployment and versatile APIs for various loss optimization. Our library is available to the open source community at https://github.com/Optimization-AI/LibAUC, to facilitate further academic research and industrial applications.

Blockwise Stochastic Variance-Reduced Methods with Parallel Speedup for Multi-Block Bilevel Optimization

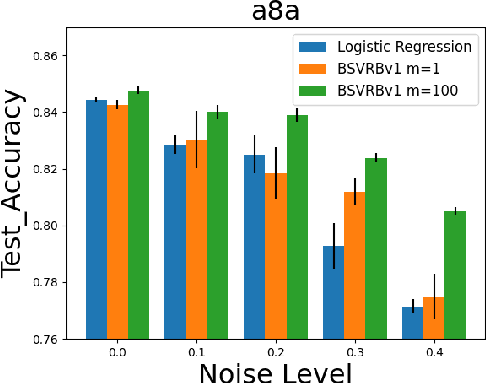
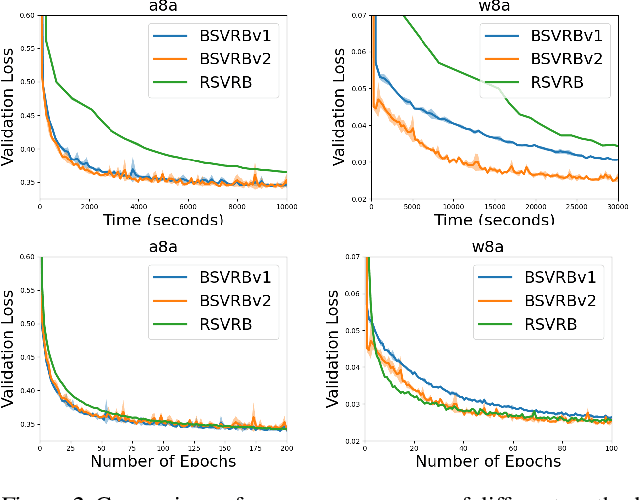
In this paper, we consider non-convex multi-block bilevel optimization (MBBO) problems, which involve $m\gg 1$ lower level problems and have important applications in machine learning. Designing a stochastic gradient and controlling its variance is more intricate due to the hierarchical sampling of blocks and data and the unique challenge of estimating hyper-gradient. We aim to achieve three nice properties for our algorithm: (a) matching the state-of-the-art complexity of standard BO problems with a single block; (b) achieving parallel speedup by sampling $I$ blocks and sampling $B$ samples for each sampled block per-iteration; (c) avoiding the computation of the inverse of a high-dimensional Hessian matrix estimator. However, it is non-trivial to achieve all of these by observing that existing works only achieve one or two of these properties. To address the involved challenges for achieving (a, b, c), we propose two stochastic algorithms by using advanced blockwise variance-reduction techniques for tracking the Hessian matrices (for low-dimensional problems) or the Hessian-vector products (for high-dimensional problems), and prove an iteration complexity of $O(\frac{m\epsilon^{-3}\mathbb{I}(I<m)}{I\sqrt{I}} + \frac{m\epsilon^{-3}}{I\sqrt{B}})$ for finding an $\epsilon$-stationary point under appropriate conditions. We also conduct experiments to verify the effectiveness of the proposed algorithms comparing with existing MBBO algorithms.

Not All Semantics are Created Equal: Contrastive Self-supervised Learning with Automatic Temperature Individualization

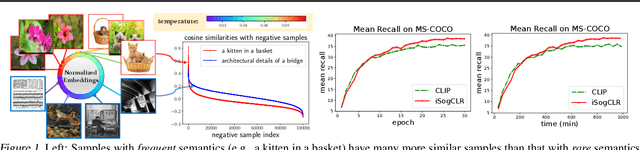
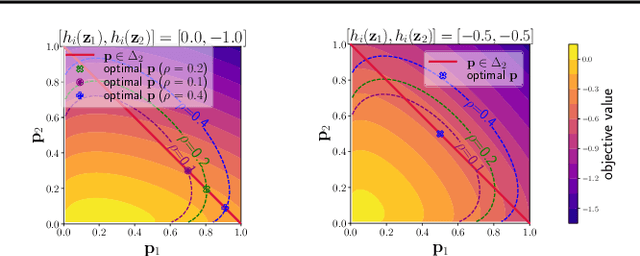
In this paper, we aim to optimize a contrastive loss with individualized temperatures in a principled and systematic manner for self-supervised learning. The common practice of using a global temperature parameter $\tau$ ignores the fact that ``not all semantics are created equal", meaning that different anchor data may have different numbers of samples with similar semantics, especially when data exhibits long-tails. First, we propose a new robust contrastive loss inspired by distributionally robust optimization (DRO), providing us an intuition about the effect of $\tau$ and a mechanism for automatic temperature individualization. Then, we propose an efficient stochastic algorithm for optimizing the robust contrastive loss with a provable convergence guarantee without using large mini-batch sizes. Theoretical and experimental results show that our algorithm automatically learns a suitable $\tau$ for each sample. Specifically, samples with frequent semantics use large temperatures to keep local semantic structures, while samples with rare semantics use small temperatures to induce more separable features. Our method not only outperforms prior strong baselines (e.g., SimCLR, CLIP) on unimodal and bimodal datasets with larger improvements on imbalanced data but also is less sensitive to hyper-parameters. To our best knowledge, this is the first methodical approach to optimizing a contrastive loss with individualized temperatures.

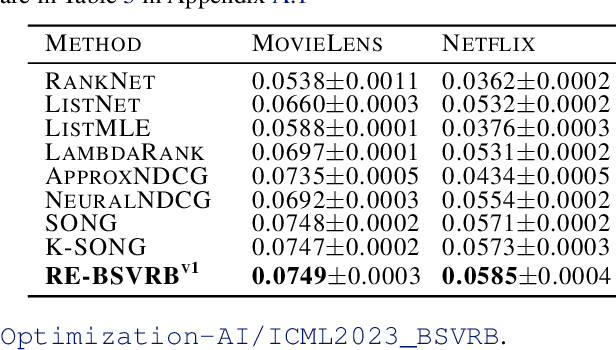
Large-scale Stochastic Optimization of NDCG Surrogates for Deep Learning with Provable Convergence

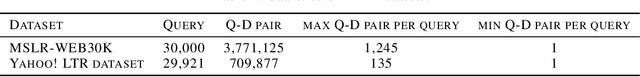
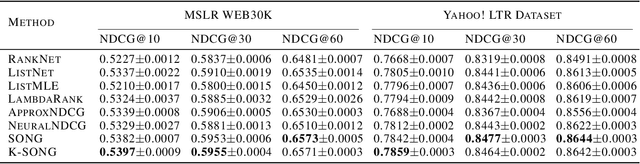
NDCG, namely Normalized Discounted Cumulative Gain, is a widely used ranking metric in information retrieval and machine learning. However, efficient and provable stochastic methods for maximizing NDCG are still lacking, especially for deep models. In this paper, we propose a principled approach to optimize NDCG and its top-$K$ variant. First, we formulate a novel compositional optimization problem for optimizing the NDCG surrogate, and a novel bilevel compositional optimization problem for optimizing the top-$K$ NDCG surrogate. Then, we develop efficient stochastic algorithms with provable convergence guarantees for the non-convex objectives. Different from existing NDCG optimization methods, the per-iteration complexity of our algorithms scales with the mini-batch size instead of the number of total items. To improve the effectiveness for deep learning, we further propose practical strategies by using initial warm-up and stop gradient operator. Experimental results on multiple datasets demonstrate that our methods outperform prior ranking approaches in terms of NDCG. To the best of our knowledge, this is the first time that stochastic algorithms are proposed to optimize NDCG with a provable convergence guarantee.