Efficient and Effective Implicit Dynamic Graph Neural Network

Implicit graph neural networks have gained popularity in recent years as they capture long-range dependencies while improving predictive performance in static graphs. Despite the tussle between performance degradation due to the oversmoothing of learned embeddings and long-range dependency being more pronounced in dynamic graphs, as features are aggregated both across neighborhood and time, no prior work has proposed an implicit graph neural model in a dynamic setting. In this paper, we present Implicit Dynamic Graph Neural Network (IDGNN) a novel implicit neural network for dynamic graphs which is the first of its kind. A key characteristic of IDGNN is that it demonstrably is well-posed, i.e., it is theoretically guaranteed to have a fixed-point representation. We then demonstrate that the standard iterative algorithm often used to train implicit models is computationally expensive in our dynamic setting as it involves computing gradients, which themselves have to be estimated in an iterative manner. To overcome this, we pose an equivalent bilevel optimization problem and propose an efficient single-loop training algorithm that avoids iterative computation by maintaining moving averages of key components of the gradients. We conduct extensive experiments on real-world datasets on both classification and regression tasks to demonstrate the superiority of our approach over the state-of-the-art baselines. We also demonstrate that our bi-level optimization framework maintains the performance of the expensive iterative algorithm while obtaining up to \textbf{1600x} speed-up.

SpatialRank: Urban Event Ranking with NDCG Optimization on Spatiotemporal Data

The problem of urban event ranking aims at predicting the top-k most risky locations of future events such as traffic accidents and crimes. This problem is of fundamental importance to public safety and urban administration especially when limited resources are available. The problem is, however, challenging due to complex and dynamic spatio-temporal correlations between locations, uneven distribution of urban events in space, and the difficulty to correctly rank nearby locations with similar features. Prior works on event forecasting mostly aim at accurately predicting the actual risk score or counts of events for all the locations. Rankings obtained as such usually have low quality due to prediction errors. Learning-to-rank methods directly optimize measures such as Normalized Discounted Cumulative Gain (NDCG), but cannot handle the spatiotemporal autocorrelation existing among locations. In this paper, we bridge the gap by proposing a novel spatial event ranking approach named SpatialRank. SpatialRank features adaptive graph convolution layers that dynamically learn the spatiotemporal dependencies across locations from data. In addition, the model optimizes through surrogates a hybrid NDCG loss with a spatial component to better rank neighboring spatial locations. We design an importance-sampling with a spatial filtering algorithm to effectively evaluate the loss during training. Comprehensive experiments on three real-world datasets demonstrate that SpatialRank can effectively identify the top riskiest locations of crimes and traffic accidents and outperform state-of-art methods in terms of NDCG by up to 12.7%.

Multi-block Min-max Bilevel Optimization with Applications in Multi-task Deep AUC Maximization

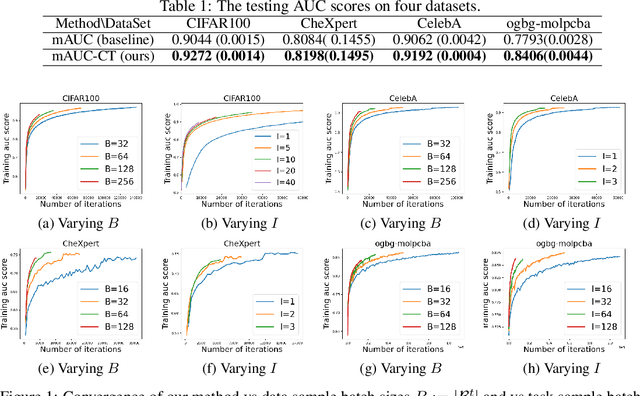
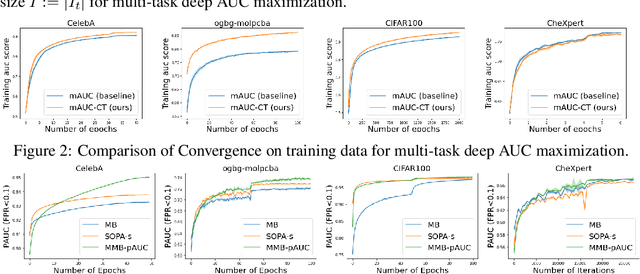
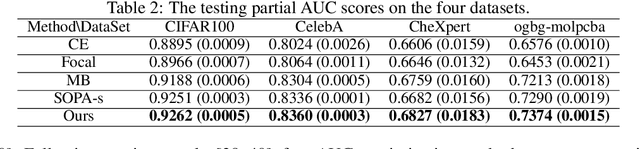
In this paper, we study multi-block min-max bilevel optimization problems, where the upper level is non-convex strongly-concave minimax objective and the lower level is a strongly convex objective, and there are multiple blocks of dual variables and lower level problems. Due to the intertwined multi-block min-max bilevel structure, the computational cost at each iteration could be prohibitively high, especially with a large number of blocks. To tackle this challenge, we present a single-loop randomized stochastic algorithm, which requires updates for only a constant number of blocks at each iteration. Under some mild assumptions on the problem, we establish its sample complexity of $\mathcal{O}(1/\epsilon^4)$ for finding an $\epsilon$-stationary point. This matches the optimal complexity for solving stochastic nonconvex optimization under a general unbiased stochastic oracle model. Moreover, we provide two applications of the proposed method in multi-task deep AUC (area under ROC curve) maximization and multi-task deep partial AUC maximization. Experimental results validate our theory and demonstrate the effectiveness of our method on problems with hundreds of tasks.

Large-scale Stochastic Optimization of NDCG Surrogates for Deep Learning with Provable Convergence

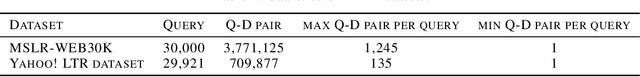
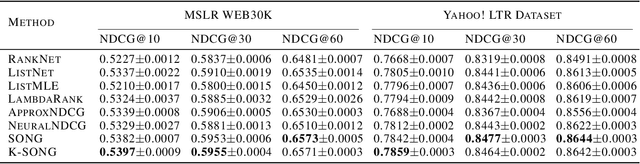
NDCG, namely Normalized Discounted Cumulative Gain, is a widely used ranking metric in information retrieval and machine learning. However, efficient and provable stochastic methods for maximizing NDCG are still lacking, especially for deep models. In this paper, we propose a principled approach to optimize NDCG and its top-$K$ variant. First, we formulate a novel compositional optimization problem for optimizing the NDCG surrogate, and a novel bilevel compositional optimization problem for optimizing the top-$K$ NDCG surrogate. Then, we develop efficient stochastic algorithms with provable convergence guarantees for the non-convex objectives. Different from existing NDCG optimization methods, the per-iteration complexity of our algorithms scales with the mini-batch size instead of the number of total items. To improve the effectiveness for deep learning, we further propose practical strategies by using initial warm-up and stop gradient operator. Experimental results on multiple datasets demonstrate that our methods outperform prior ranking approaches in terms of NDCG. To the best of our knowledge, this is the first time that stochastic algorithms are proposed to optimize NDCG with a provable convergence guarantee.