Efficient and Effective Implicit Dynamic Graph Neural Network

Implicit graph neural networks have gained popularity in recent years as they capture long-range dependencies while improving predictive performance in static graphs. Despite the tussle between performance degradation due to the oversmoothing of learned embeddings and long-range dependency being more pronounced in dynamic graphs, as features are aggregated both across neighborhood and time, no prior work has proposed an implicit graph neural model in a dynamic setting. In this paper, we present Implicit Dynamic Graph Neural Network (IDGNN) a novel implicit neural network for dynamic graphs which is the first of its kind. A key characteristic of IDGNN is that it demonstrably is well-posed, i.e., it is theoretically guaranteed to have a fixed-point representation. We then demonstrate that the standard iterative algorithm often used to train implicit models is computationally expensive in our dynamic setting as it involves computing gradients, which themselves have to be estimated in an iterative manner. To overcome this, we pose an equivalent bilevel optimization problem and propose an efficient single-loop training algorithm that avoids iterative computation by maintaining moving averages of key components of the gradients. We conduct extensive experiments on real-world datasets on both classification and regression tasks to demonstrate the superiority of our approach over the state-of-the-art baselines. We also demonstrate that our bi-level optimization framework maintains the performance of the expensive iterative algorithm while obtaining up to \textbf{1600x} speed-up.

Distributionally Robust Fair Principal Components via Geodesic Descents

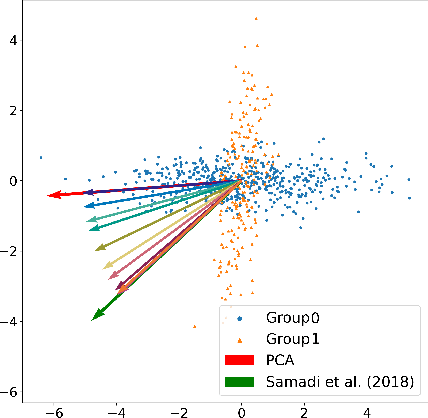
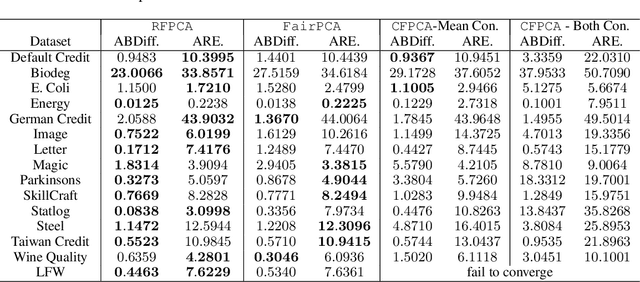
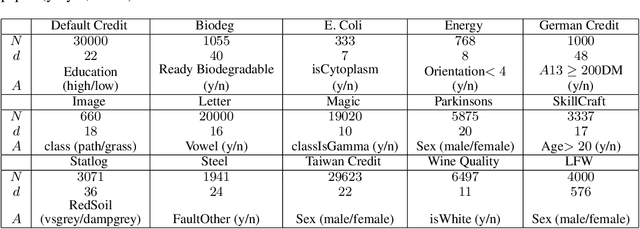
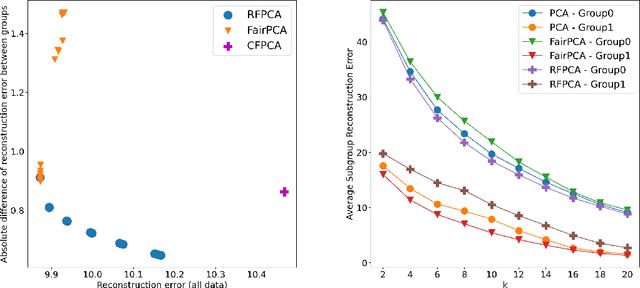
Principal component analysis is a simple yet useful dimensionality reduction technique in modern machine learning pipelines. In consequential domains such as college admission, healthcare and credit approval, it is imperative to take into account emerging criteria such as the fairness and the robustness of the learned projection. In this paper, we propose a distributionally robust optimization problem for principal component analysis which internalizes a fairness criterion in the objective function. The learned projection thus balances the trade-off between the total reconstruction error and the reconstruction error gap between subgroups, taken in the min-max sense over all distributions in a moment-based ambiguity set. The resulting optimization problem over the Stiefel manifold can be efficiently solved by a Riemannian subgradient descent algorithm with a sub-linear convergence rate. Our experimental results on real-world datasets show the merits of our proposed method over state-of-the-art baselines.