Test-time Diverse Reasoning by Riemannian Activation Steering

Best-of-$N$ reasoning improves the accuracy of language models in solving complex tasks by sampling multiple candidate solutions and then selecting the best one based on some criteria. A critical bottleneck for this strategy is the output diversity limit, which occurs when the model generates similar outputs despite stochastic sampling, and hence recites the same error. To address this lack of variance in reasoning paths, we propose a novel unsupervised activation steering strategy that simultaneously optimizes the steering vectors for multiple reasoning trajectories at test time. At any synchronization anchor along the batch generation process, we find the steering vectors that maximize the total volume spanned by all possible intervened activation subsets. We demonstrate that these steering vectors can be determined by solving a Riemannian optimization problem over the product of spheres with a log-determinant objective function. We then use a Riemannian block-coordinate descent algorithm with a well-tuned learning rate to obtain a stationary point of the problem, and we apply these steering vectors until the generation process reaches the subsequent synchronization anchor. Empirical evaluations on popular mathematical benchmarks demonstrate that our test-time Riemannian activation steering strategy outperforms vanilla sampling techniques in terms of generative diversity and solution accuracy.

Pseudo-Asynchronous Local SGD: Robust and Efficient Data-Parallel Training

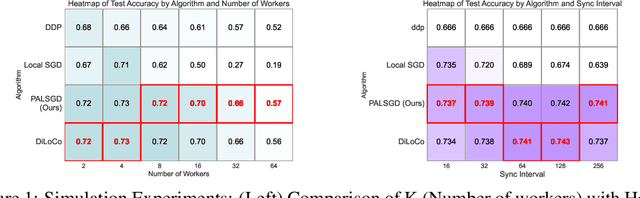
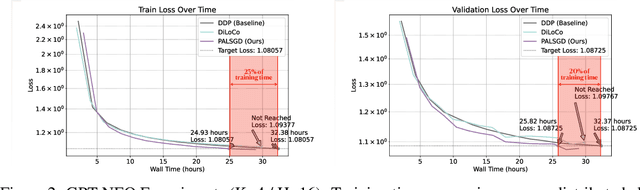
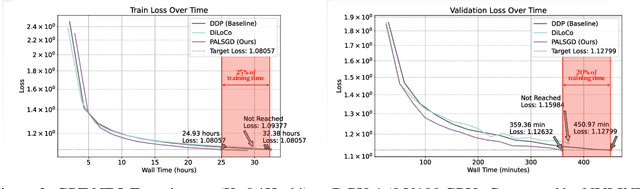
Following AI scaling trends, frontier models continue to grow in size and continue to be trained on larger datasets. Training these models requires huge investments in exascale computational resources, which has in turn driven development of distributed deep learning methods. Data parallelism is an essential approach to speed up training, but it requires frequent global communication between workers, which can bottleneck training at the largest scales. In this work, we propose a method called Pseudo-Asynchronous Local SGD (PALSGD) to improve the efficiency of data-parallel training. PALSGD is an extension of Local SGD (Stich, 2018) and DiLoCo (Douillard et al., 2023), designed to further reduce communication frequency by introducing a pseudo-synchronization mechanism. PALSGD allows the use of longer synchronization intervals compared to standard Local SGD. Despite the reduced communication frequency, the pseudo-synchronization approach ensures that model consistency is maintained, leading to performance results comparable to those achieved with more frequent synchronization. Furthermore, we provide a theoretical analysis of PALSGD, establishing its convergence and deriving its convergence rate. This analysis offers insights into the algorithm's behavior and performance guarantees. We evaluated PALSGD on image classification and language modeling tasks. Our results show that PALSGD achieves better performance in less time compared to existing methods like Distributed Data Parallel (DDP), and DiLoCo. Notably, PALSGD trains 18.4% faster than DDP on ImageNet-1K with ResNet-50, 24.4% faster than DDP on TinyStories with GPT-Neo125M, and 21.1% faster than DDP on TinyStories with GPT-Neo-8M.

A Geometric Unification of Distributionally Robust Covariance Estimators: Shrinking the Spectrum by Inflating the Ambiguity Set

The state-of-the-art methods for estimating high-dimensional covariance matrices all shrink the eigenvalues of the sample covariance matrix towards a data-insensitive shrinkage target. The underlying shrinkage transformation is either chosen heuristically - without compelling theoretical justification - or optimally in view of restrictive distributional assumptions. In this paper, we propose a principled approach to construct covariance estimators without imposing restrictive assumptions. That is, we study distributionally robust covariance estimation problems that minimize the worst-case Frobenius error with respect to all data distributions close to a nominal distribution, where the proximity of distributions is measured via a divergence on the space of covariance matrices. We identify mild conditions on this divergence under which the resulting minimizers represent shrinkage estimators. We show that the corresponding shrinkage transformations are intimately related to the geometrical properties of the underlying divergence. We also prove that our robust estimators are efficiently computable and asymptotically consistent and that they enjoy finite-sample performance guarantees. We exemplify our general methodology by synthesizing explicit estimators induced by the Kullback-Leibler, Fisher-Rao, and Wasserstein divergences. Numerical experiments based on synthetic and real data show that our robust estimators are competitive with state-of-the-art estimators.

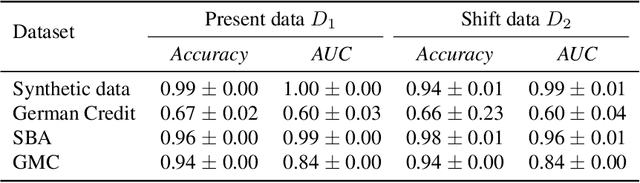
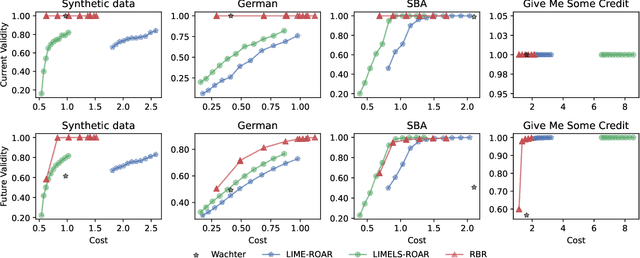
Coverage-Validity-Aware Algorithmic Recourse

Algorithmic recourse emerges as a prominent technique to promote the explainability, transparency and hence ethics of machine learning models. Existing algorithmic recourse approaches often assume an invariant predictive model; however, the predictive model is usually updated upon the arrival of new data. Thus, a recourse that is valid respective to the present model may become invalid for the future model. To resolve this issue, we propose a novel framework to generate a model-agnostic recourse that exhibits robustness to model shifts. Our framework first builds a coverage-validity-aware linear surrogate of the nonlinear (black-box) model; then, the recourse is generated with respect to the linear surrogate. We establish a theoretical connection between our coverage-validity-aware linear surrogate and the minimax probability machines (MPM). We then prove that by prescribing different covariance robustness, the proposed framework recovers popular regularizations for MPM, including the $\ell_2$-regularization and class-reweighting. Furthermore, we show that our surrogate pushes the approximate hyperplane intuitively, facilitating not only robust but also interpretable recourses. The numerical results demonstrate the usefulness and robustness of our framework.

Approximate Secular Equations for the Cubic Regularization Subproblem

The cubic regularization method (CR) is a popular algorithm for unconstrained non-convex optimization. At each iteration, CR solves a cubically regularized quadratic problem, called the cubic regularization subproblem (CRS). One way to solve the CRS relies on solving the secular equation, whose computational bottleneck lies in the computation of all eigenvalues of the Hessian matrix. In this paper, we propose and analyze a novel CRS solver based on an approximate secular equation, which requires only some of the Hessian eigenvalues and is therefore much more efficient. Two approximate secular equations (ASEs) are developed. For both ASEs, we first study the existence and uniqueness of their roots and then establish an upper bound on the gap between the root and that of the standard secular equation. Such an upper bound can in turn be used to bound the distance from the approximate CRS solution based ASEs to the true CRS solution, thus offering a theoretical guarantee for our CRS solver. A desirable feature of our CRS solver is that it requires only matrix-vector multiplication but not matrix inversion, which makes it particularly suitable for high-dimensional applications of unconstrained non-convex optimization, such as low-rank recovery and deep learning. Numerical experiments with synthetic and real data-sets are conducted to investigate the practical performance of the proposed CRS solver. Experimental results show that the proposed solver outperforms two state-of-the-art methods.

Robust Bayesian Recourse

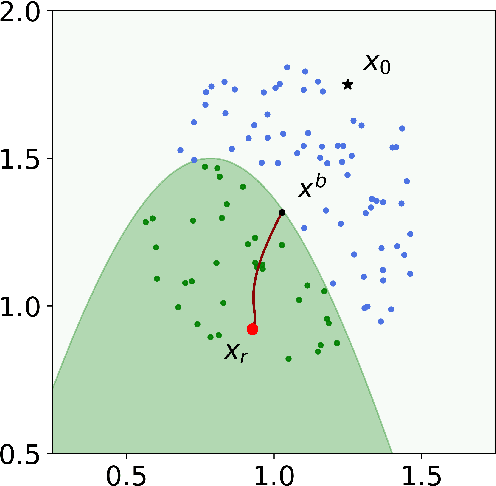
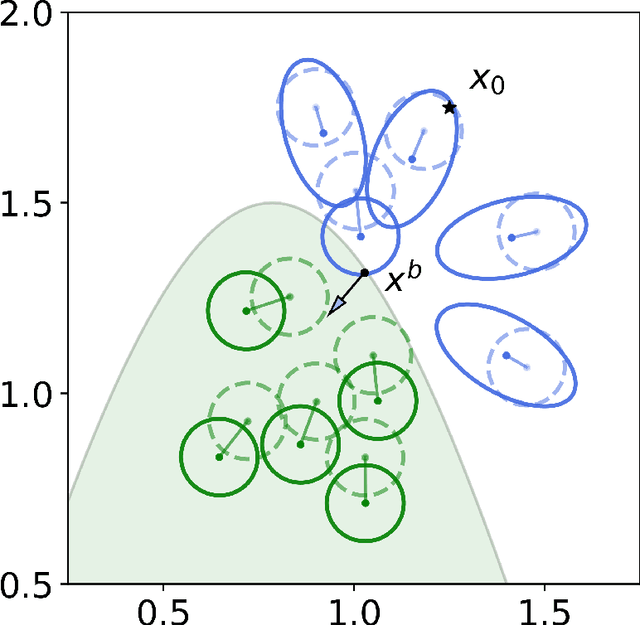
Algorithmic recourse aims to recommend an informative feedback to overturn an unfavorable machine learning decision. We introduce in this paper the Bayesian recourse, a model-agnostic recourse that minimizes the posterior probability odds ratio. Further, we present its min-max robust counterpart with the goal of hedging against future changes in the machine learning model parameters. The robust counterpart explicitly takes into account possible perturbations of the data in a Gaussian mixture ambiguity set prescribed using the optimal transport (Wasserstein) distance. We show that the resulting worst-case objective function can be decomposed into solving a series of two-dimensional optimization subproblems, and the min-max recourse finding problem is thus amenable to a gradient descent algorithm. Contrary to existing methods for generating robust recourses, the robust Bayesian recourse does not require a linear approximation step. The numerical experiment demonstrates the effectiveness of our proposed robust Bayesian recourse facing model shifts. Our code is available at https://github.com/VinAIResearch/robust-bayesian-recourse.

Distributionally Robust Fair Principal Components via Geodesic Descents

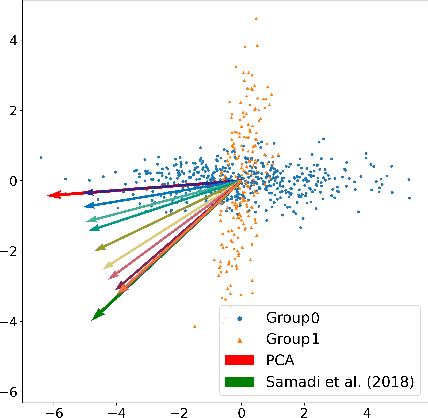
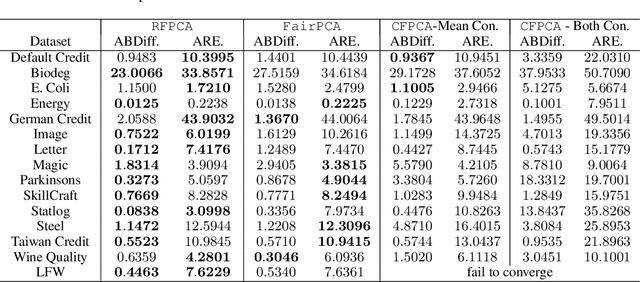
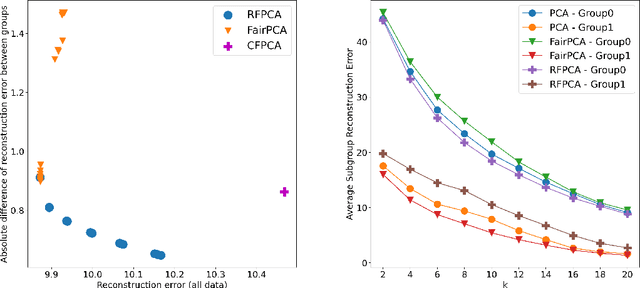
Principal component analysis is a simple yet useful dimensionality reduction technique in modern machine learning pipelines. In consequential domains such as college admission, healthcare and credit approval, it is imperative to take into account emerging criteria such as the fairness and the robustness of the learned projection. In this paper, we propose a distributionally robust optimization problem for principal component analysis which internalizes a fairness criterion in the objective function. The learned projection thus balances the trade-off between the total reconstruction error and the reconstruction error gap between subgroups, taken in the min-max sense over all distributions in a moment-based ambiguity set. The resulting optimization problem over the Stiefel manifold can be efficiently solved by a Riemannian subgradient descent algorithm with a sub-linear convergence rate. Our experimental results on real-world datasets show the merits of our proposed method over state-of-the-art baselines.

Sequential Domain Adaptation by Synthesizing Distributionally Robust Experts

Least squares estimators, when trained on a few target domain samples, may predict poorly. Supervised domain adaptation aims to improve the predictive accuracy by exploiting additional labeled training samples from a source distribution that is close to the target distribution. Given available data, we investigate novel strategies to synthesize a family of least squares estimator experts that are robust with regard to moment conditions. When these moment conditions are specified using Kullback-Leibler or Wasserstein-type divergences, we can find the robust estimators efficiently using convex optimization. We use the Bernstein online aggregation algorithm on the proposed family of robust experts to generate predictions for the sequential stream of target test samples. Numerical experiments on real data show that the robust strategies may outperform non-robust interpolations of the empirical least squares estimators.

A Unified Approach to Synchronization Problems over Subgroups of the Orthogonal Group

Given a group $\mathcal{G}$, the problem of synchronization over the group $\mathcal{G}$ is a constrained estimation problem where a collection of group elements $G^*_1, \dots, G^*_n \in \mathcal{G}$ are estimated based on noisy observations of pairwise ratios $G^*_i {G^*_j}^{-1}$ for an incomplete set of index pairs $(i,j)$. This problem has gained much attention recently and finds lots of applications due to its appearance in a wide range of scientific and engineering areas. In this paper, we consider the class of synchronization problems over a closed subgroup of the orthogonal group, which covers many instances of group synchronization problems that arise in practice. Our contributions are threefold. First, we propose a unified approach to solve this class of group synchronization problems, which consists of a suitable initialization and an iterative refinement procedure via the generalized power method. Second, we derive a master theorem on the performance guarantee of the proposed approach. Under certain conditions on the subgroup, the measurement model, the noise model and the initialization, the estimation error of the iterates of our approach decreases geometrically. As our third contribution, we study concrete examples of the subgroup (including the orthogonal group, the special orthogonal group, the permutation group and the cyclic group), the measurement model, the noise model and the initialization. The validity of the related conditions in the master theorem are proved for these specific examples. Numerical experiments are also presented. Experiment results show that our approach outperforms existing approaches in terms of computational speed, scalability and estimation error.

On Linear Optimization over Wasserstein Balls

Wasserstein balls, which contain all probability measures within a pre-specified Wasserstein distance to a reference measure, have recently enjoyed wide popularity in the distributionally robust optimization and machine learning communities to formulate and solve data-driven optimization problems with rigorous statistical guarantees. In this technical note we prove that the Wasserstein ball is weakly compact under mild conditions, and we offer necessary and sufficient conditions for the existence of optimal solutions. We also characterize the sparsity of solutions if the Wasserstein ball is centred at a discrete reference measure. In comparison with the existing literature, which has proved similar results under different conditions, our proofs are self-contained and shorter, yet mathematically rigorous, and our necessary and sufficient conditions for the existence of optimal solutions are easily verifiable in practice.