Wolfram Wiesemann
Efficient Algorithms for Robust Markov Decision Processes with $s$-Rectangular Ambiguity Sets
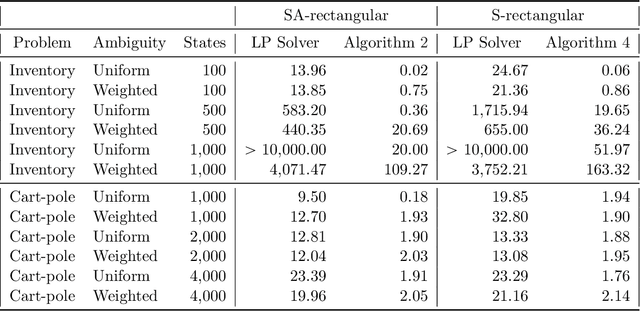
Feb 05, 2026Abstract:Robust Markov decision processes (MDPs) have attracted significant interest due to their ability to protect MDPs from poor out-of-sample performance in the presence of ambiguity. In contrast to classical MDPs, which account for stochasticity by modeling the dynamics through a stochastic process with a known transition kernel, a robust MDP additionally accounts for ambiguity by optimizing against the most adverse transition kernel from an ambiguity set constructed via historical data. In this paper, we develop a unified solution framework for a broad class of robust MDPs with $s$-rectangular ambiguity sets, where the most adverse transition probabilities are considered independently for each state. Using our algorithms, we show that $s$-rectangular robust MDPs with $1$- and $2$-norm as well as $φ$-divergence ambiguity sets can be solved several orders of magnitude faster than with state-of-the-art commercial solvers, and often only a logarithmic factor slower than classical MDPs. We demonstrate the favorable scaling properties of our algorithms on a range of synthetically generated as well as standard benchmark instances.
It's All in the Mix: Wasserstein Machine Learning with Mixed Features
Dec 19, 2023Abstract:Problem definition: The recent advent of data-driven and end-to-end decision-making across different areas of operations management has led to an ever closer integration of prediction models from machine learning and optimization models from operations research. A key challenge in this context is the presence of estimation errors in the prediction models, which tend to be amplified by the subsequent optimization model -- a phenomenon that is often referred to as the Optimizer's Curse or the Error-Maximization Effect of Optimization. Methodology/results: A contemporary approach to combat such estimation errors is offered by distributionally robust problem formulations that consider all data-generating distributions close to the empirical distribution derived from historical samples, where `closeness' is determined by the Wasserstein distance. While those techniques show significant promise in problems where all input features are continuous, they scale exponentially when binary and/or categorical features are present. This paper demonstrates that such mixed-feature problems can indeed be solved in polynomial time. We present a practically efficient algorithm to solve mixed-feature problems, and we compare our method against alternative techniques both theoretically and empirically on standard benchmark instances. Managerial implications: Data-driven operations management problems often involve prediction models with discrete features. We develop and analyze a methodology that faithfully accounts for the presence of discrete features, and we demonstrate that our approach can significantly outperform existing methods that are agnostic to the presence of discrete features, both theoretically and across standard benchmark instances.
Streamlining Energy Transition Scenarios to Key Policy Decisions
Nov 11, 2023Abstract:Uncertainties surrounding the energy transition often lead modelers to present large sets of scenarios that are challenging for policymakers to interpret and act upon. An alternative approach is to define a few qualitative storylines from stakeholder discussions, which can be affected by biases and infeasibilities. Leveraging decision trees, a popular machine-learning technique, we derive interpretable storylines from many quantitative scenarios and show how the key decisions in the energy transition are interlinked. Specifically, our results demonstrate that choosing a high deployment of renewables and sector coupling makes global decarbonization scenarios robust against uncertainties in climate sensitivity and demand. Also, the energy transition to a fossil-free Europe is primarily determined by choices on the roles of bioenergy, storage, and heat electrification. Our transferrable approach translates vast energy model results into a small set of critical decisions, guiding decision-makers in prioritizing the key factors that will shape the energy transition.
Differential Privacy via Distributionally Robust Optimization
Apr 25, 2023Abstract:In recent years, differential privacy has emerged as the de facto standard for sharing statistics of datasets while limiting the disclosure of private information about the involved individuals. This is achieved by randomly perturbing the statistics to be published, which in turn leads to a privacy-accuracy trade-off: larger perturbations provide stronger privacy guarantees, but they result in less accurate statistics that offer lower utility to the recipients. Of particular interest are therefore optimal mechanisms that provide the highest accuracy for a pre-selected level of privacy. To date, work in this area has focused on specifying families of perturbations a priori and subsequently proving their asymptotic and/or best-in-class optimality. In this paper, we develop a class of mechanisms that enjoy non-asymptotic and unconditional optimality guarantees. To this end, we formulate the mechanism design problem as an infinite-dimensional distributionally robust optimization problem. We show that the problem affords a strong dual, and we exploit this duality to develop converging hierarchies of finite-dimensional upper and lower bounding problems. Our upper (primal) bounds correspond to implementable perturbations whose suboptimality can be bounded by our lower (dual) bounds. Both bounding problems can be solved within seconds via cutting plane techniques that exploit the inherent problem structure. Our numerical experiments demonstrate that our perturbations can outperform the previously best results from the literature on artificial as well as standard benchmark problems.
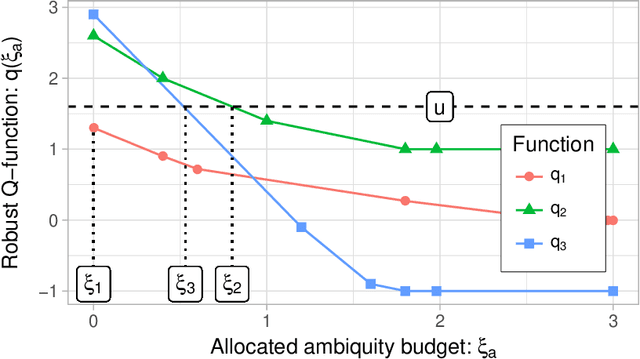
Robust Phi-Divergence MDPs
May 27, 2022
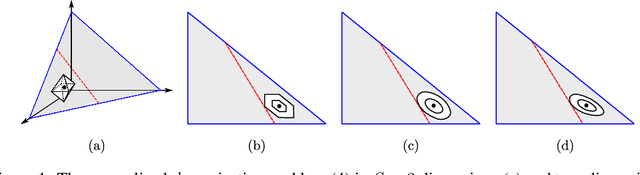

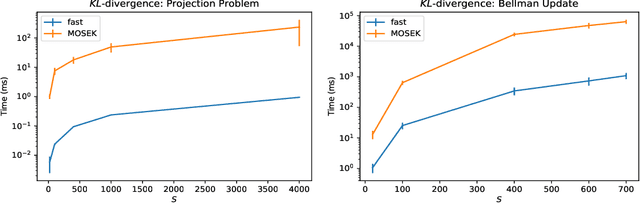
Abstract:In recent years, robust Markov decision processes (MDPs) have emerged as a prominent modeling framework for dynamic decision problems affected by uncertainty. In contrast to classical MDPs, which only account for stochasticity by modeling the dynamics through a stochastic process with a known transition kernel, robust MDPs additionally account for ambiguity by optimizing in view of the most adverse transition kernel from a prescribed ambiguity set. In this paper, we develop a novel solution framework for robust MDPs with s-rectangular ambiguity sets that decomposes the problem into a sequence of robust Bellman updates and simplex projections. Exploiting the rich structure present in the simplex projections corresponding to phi-divergence ambiguity sets, we show that the associated s-rectangular robust MDPs can be solved substantially faster than with state-of-the-art commercial solvers as well as a recent first-order solution scheme, thus rendering them attractive alternatives to classical MDPs in practical applications.
Partial Policy Iteration for L1-Robust Markov Decision Processes
Jun 16, 2020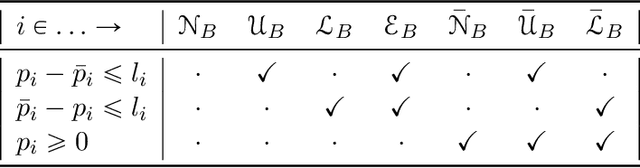
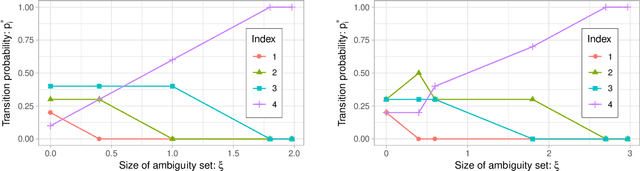
Abstract:Robust Markov decision processes (MDPs) allow to compute reliable solutions for dynamic decision problems whose evolution is modeled by rewards and partially-known transition probabilities. Unfortunately, accounting for uncertainty in the transition probabilities significantly increases the computational complexity of solving robust MDPs, which severely limits their scalability. This paper describes new efficient algorithms for solving the common class of robust MDPs with s- and sa-rectangular ambiguity sets defined by weighted $L_1$ norms. We propose partial policy iteration, a new, efficient, flexible, and general policy iteration scheme for robust MDPs. We also propose fast methods for computing the robust Bellman operator in quasi-linear time, nearly matching the linear complexity the non-robust Bellman operator. Our experimental results indicate that the proposed methods are many orders of magnitude faster than the state-of-the-art approach which uses linear programming solvers combined with a robust value iteration.
On Linear Optimization over Wasserstein Balls
Apr 15, 2020Abstract:Wasserstein balls, which contain all probability measures within a pre-specified Wasserstein distance to a reference measure, have recently enjoyed wide popularity in the distributionally robust optimization and machine learning communities to formulate and solve data-driven optimization problems with rigorous statistical guarantees. In this technical note we prove that the Wasserstein ball is weakly compact under mild conditions, and we offer necessary and sufficient conditions for the existence of optimal solutions. We also characterize the sparsity of solutions if the Wasserstein ball is centred at a discrete reference measure. In comparison with the existing literature, which has proved similar results under different conditions, our proofs are self-contained and shorter, yet mathematically rigorous, and our necessary and sufficient conditions for the existence of optimal solutions are easily verifiable in practice.
Optimistic Distributionally Robust Optimization for Nonparametric Likelihood Approximation
Oct 23, 2019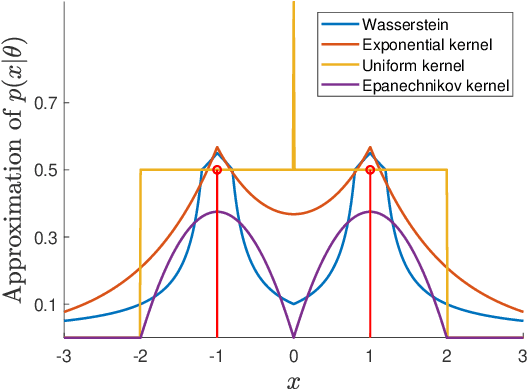
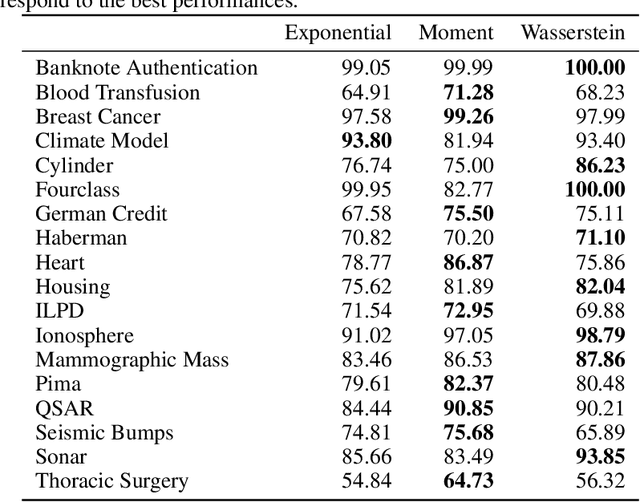
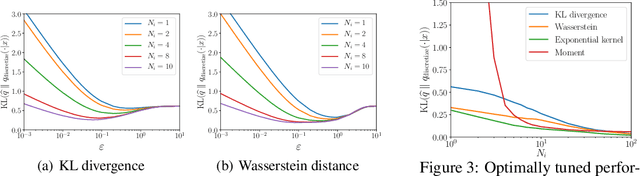
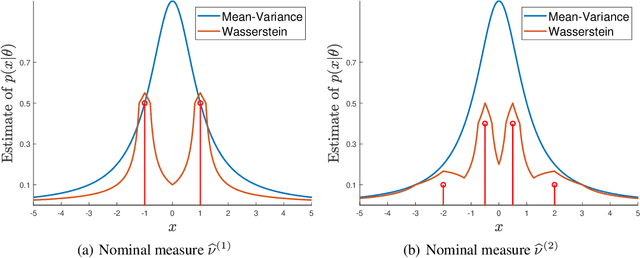
Abstract:The likelihood function is a fundamental component in Bayesian statistics. However, evaluating the likelihood of an observation is computationally intractable in many applications. In this paper, we propose a non-parametric approximation of the likelihood that identifies a probability measure which lies in the neighborhood of the nominal measure and that maximizes the probability of observing the given sample point. We show that when the neighborhood is constructed by the Kullback-Leibler divergence, by moment conditions or by the Wasserstein distance, then our \textit{optimistic likelihood} can be determined through the solution of a convex optimization problem, and it admits an analytical expression in particular cases. We also show that the posterior inference problem with our optimistic likelihood approximation enjoys strong theoretical performance guarantees, and it performs competitively in a probabilistic classification task.
Calculating Optimistic Likelihoods Using (Geodesically) Convex Optimization
Oct 17, 2019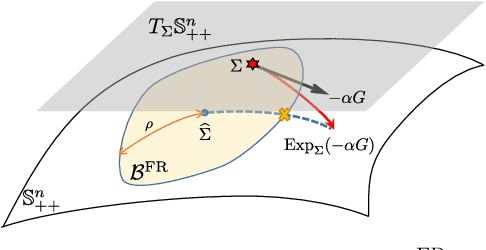
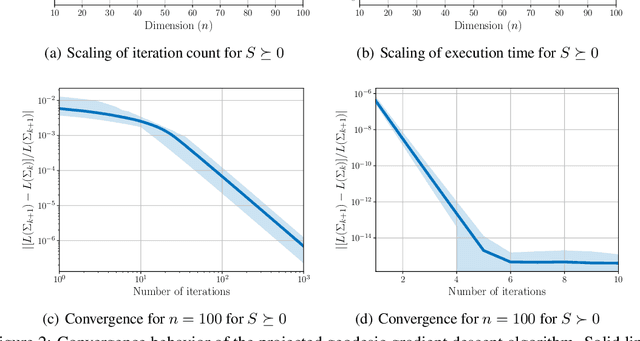
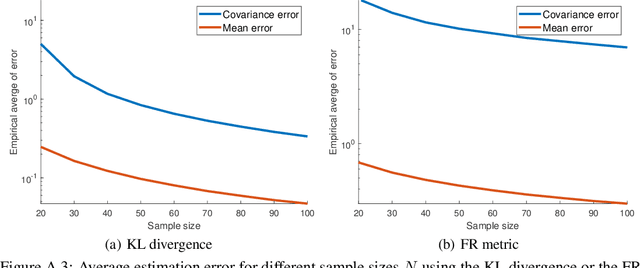
Abstract:A fundamental problem arising in many areas of machine learning is the evaluation of the likelihood of a given observation under different nominal distributions. Frequently, these nominal distributions are themselves estimated from data, which makes them susceptible to estimation errors. We thus propose to replace each nominal distribution with an ambiguity set containing all distributions in its vicinity and to evaluate an \emph{optimistic likelihood}, that is, the maximum of the likelihood over all distributions in the ambiguity set. When the proximity of distributions is quantified by the Fisher-Rao distance or the Kullback-Leibler divergence, the emerging optimistic likelihoods can be computed efficiently using either geodesic or standard convex optimization techniques. We showcase the advantages of working with optimistic likelihoods on a classification problem using synthetic as well as empirical data.
Size Matters: Cardinality-Constrained Clustering and Outlier Detection via Conic Optimization
Oct 05, 2017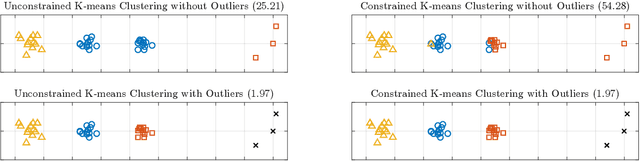

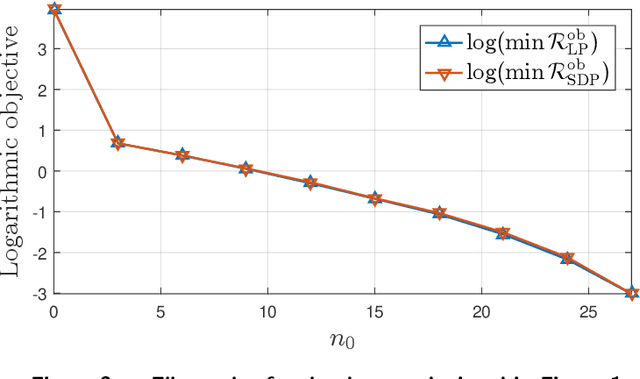
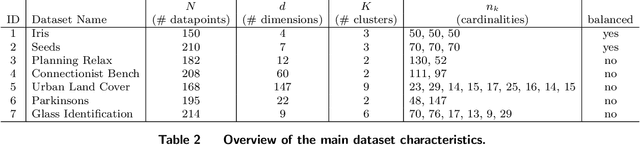
Abstract:Plain vanilla K-means clustering is prone to produce unbalanced clusters and suffers from outlier sensitivity. To mitigate both shortcomings, we formulate a joint outlier detection and clustering problem, which assigns a prescribed number of datapoints to an auxiliary outlier cluster and performs cardinality-constrained K-means clustering on the residual dataset. We cast this problem as a mixed-integer linear program (MILP) that admits tractable semidefinite and linear programming relaxations. We propose deterministic rounding schemes that transform the relaxed solutions to feasible solutions for the MILP. We also prove that these solutions are optimal in the MILP if a cluster separation condition holds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge