Policy Gradient for Robust Markov Decision Processes

We develop a generic policy gradient method with the global optimality guarantee for robust Markov Decision Processes (MDPs). While policy gradient methods are widely used for solving dynamic decision problems due to their scalable and efficient nature, adapting these methods to account for model ambiguity has been challenging, often making it impractical to learn robust policies. This paper introduces a novel policy gradient method, Double-Loop Robust Policy Mirror Descent (DRPMD), for solving robust MDPs. DRPMD employs a general mirror descent update rule for the policy optimization with adaptive tolerance per iteration, guaranteeing convergence to a globally optimal policy. We provide a comprehensive analysis of DRPMD, including new convergence results under both direct and softmax parameterizations, and provide novel insights into the inner problem solution through Transition Mirror Ascent (TMA). Additionally, we propose innovative parametric transition kernels for both discrete and continuous state-action spaces, broadening the applicability of our approach. Empirical results validate the robustness and global convergence of DRPMD across various challenging robust MDP settings.

Wasserstein Distributionally Robust Chance Constrained Trajectory Optimization for Mobile Robots within Uncertain Safe Corridor

Safe corridor-based Trajectory Optimization (TO) presents an appealing approach for collision-free path planning of autonomous robots, offering global optimality through its convex formulation. The safe corridor is constructed based on the perceived map, however, the non-ideal perception induces uncertainty, which is rarely considered in trajectory generation. In this paper, we propose Distributionally Robust Safe Corridor Constraints (DRSCCs) to consider the uncertainty of the safe corridor. Then, we integrate DRSCCs into the trajectory optimization framework using Bernstein basis polynomials. Theoretically, we rigorously prove that the trajectory optimization problem incorporating DRSCCs is equivalent to a computationally efficient, convex quadratic program. Compared to the nominal TO, our method enhances navigation safety by significantly reducing the infeasible motions in presence of uncertainty. Moreover, the proposed approach is validated through two robotic applications, a micro Unmanned Aerial Vehicle (UAV) and a quadruped robot Unitree A1.

Risk-Averse MDPs under Reward Ambiguity

We propose a distributionally robust return-risk model for Markov decision processes (MDPs) under risk and reward ambiguity. The proposed model optimizes the weighted average of mean and percentile performances, and it covers the distributionally robust MDPs and the distributionally robust chance-constrained MDPs (both under reward ambiguity) as special cases. By considering that the unknown reward distribution lies in a Wasserstein ambiguity set, we derive the tractable reformulation for our model. In particular, we show that that the return-risk model can also account for risk from uncertain transition kernel when one only seeks deterministic policies, and that a distributionally robust MDP under the percentile criterion can be reformulated as its nominal counterpart at an adjusted risk level. A scalable first-order algorithm is designed to solve large-scale problems, and we demonstrate the advantages of our proposed model and algorithm through numerical experiments.

On the Convergence of Policy Gradient in Robust MDPs

Robust Markov decision processes (RMDPs) are promising models that provide reliable policies under ambiguities in model parameters. As opposed to nominal Markov decision processes (MDPs), however, the state-of-the-art solution methods for RMDPs are limited to value-based methods, such as value iteration and policy iteration. This paper proposes Double-Loop Robust Policy Gradient (DRPG), the first generic policy gradient method for RMDPs with a global convergence guarantee in tabular problems. Unlike value-based methods, DRPG does not rely on dynamic programming techniques. In particular, the inner-loop robust policy evaluation problem is solved via projected gradient descent. Finally, our experimental results demonstrate the performance of our algorithm and verify our theoretical guarantees.

Robust Phi-Divergence MDPs

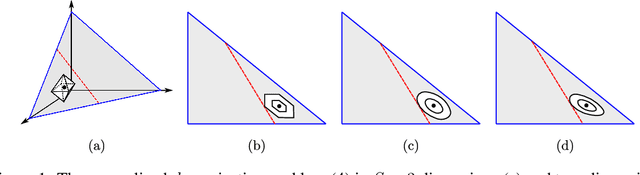
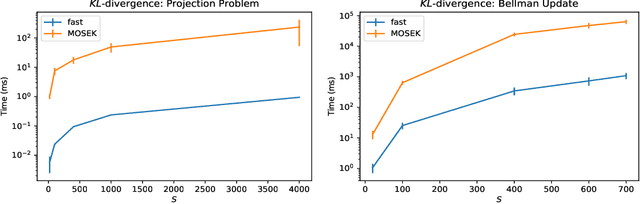
In recent years, robust Markov decision processes (MDPs) have emerged as a prominent modeling framework for dynamic decision problems affected by uncertainty. In contrast to classical MDPs, which only account for stochasticity by modeling the dynamics through a stochastic process with a known transition kernel, robust MDPs additionally account for ambiguity by optimizing in view of the most adverse transition kernel from a prescribed ambiguity set. In this paper, we develop a novel solution framework for robust MDPs with s-rectangular ambiguity sets that decomposes the problem into a sequence of robust Bellman updates and simplex projections. Exploiting the rich structure present in the simplex projections corresponding to phi-divergence ambiguity sets, we show that the associated s-rectangular robust MDPs can be solved substantially faster than with state-of-the-art commercial solvers as well as a recent first-order solution scheme, thus rendering them attractive alternatives to classical MDPs in practical applications.

Partial Policy Iteration for L1-Robust Markov Decision Processes

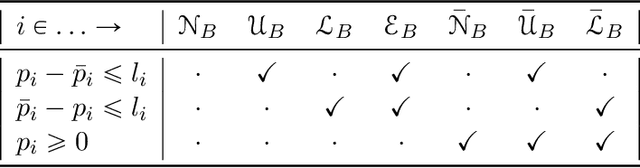
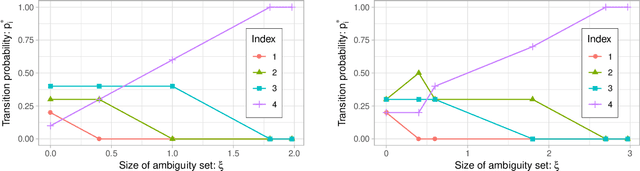
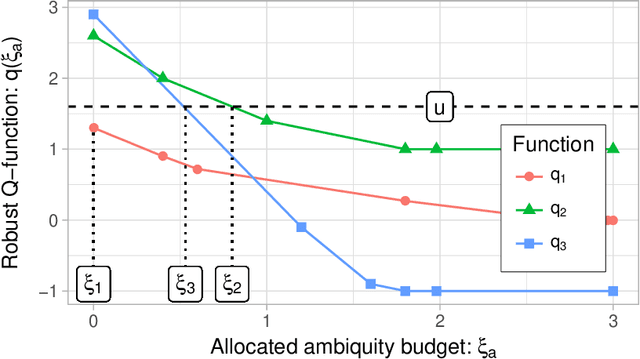
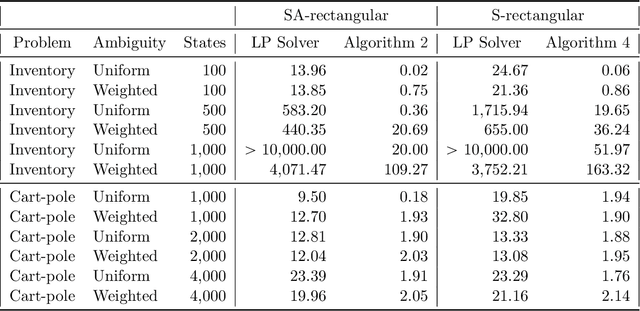
Robust Markov decision processes (MDPs) allow to compute reliable solutions for dynamic decision problems whose evolution is modeled by rewards and partially-known transition probabilities. Unfortunately, accounting for uncertainty in the transition probabilities significantly increases the computational complexity of solving robust MDPs, which severely limits their scalability. This paper describes new efficient algorithms for solving the common class of robust MDPs with s- and sa-rectangular ambiguity sets defined by weighted $L_1$ norms. We propose partial policy iteration, a new, efficient, flexible, and general policy iteration scheme for robust MDPs. We also propose fast methods for computing the robust Bellman operator in quasi-linear time, nearly matching the linear complexity the non-robust Bellman operator. Our experimental results indicate that the proposed methods are many orders of magnitude faster than the state-of-the-art approach which uses linear programming solvers combined with a robust value iteration.

Fully Automatic Myocardial Segmentation of Contrast Echocardiography Sequence Using Random Forests Guided by Shape Model

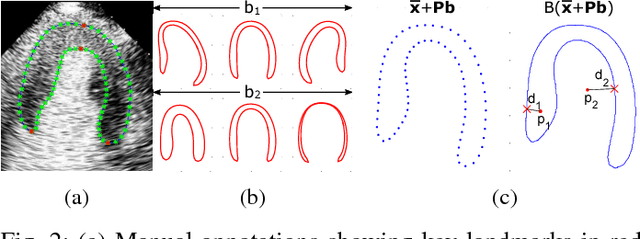
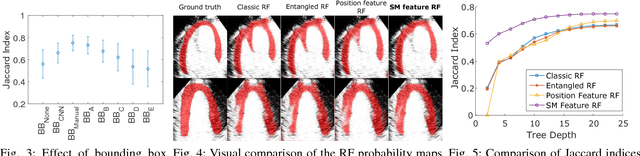
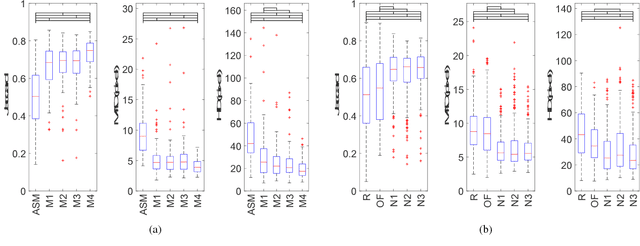
Myocardial contrast echocardiography (MCE) is an imaging technique that assesses left ventricle function and myocardial perfusion for the detection of coronary artery diseases. Automatic MCE perfusion quantification is challenging and requires accurate segmentation of the myocardium from noisy and time-varying images. Random forests (RF) have been successfully applied to many medical image segmentation tasks. However, the pixel-wise RF classifier ignores contextual relationships between label outputs of individual pixels. RF which only utilizes local appearance features is also susceptible to data suffering from large intensity variations. In this paper, we demonstrate how to overcome the above limitations of classic RF by presenting a fully automatic segmentation pipeline for myocardial segmentation in full-cycle 2D MCE data. Specifically, a statistical shape model is used to provide shape prior information that guide the RF segmentation in two ways. First, a novel shape model (SM) feature is incorporated into the RF framework to generate a more accurate RF probability map. Second, the shape model is fitted to the RF probability map to refine and constrain the final segmentation to plausible myocardial shapes. We further improve the performance by introducing a bounding box detection algorithm as a preprocessing step in the segmentation pipeline. Our approach on 2D image is further extended to 2D+t sequence which ensures temporal consistency in the resultant sequence segmentations. When evaluated on clinical MCE data, our proposed method achieves notable improvement in segmentation accuracy and outperforms other state-of-the-art methods including the classic RF and its variants, active shape model and image registration.

Myocardial Segmentation of Contrast Echocardiograms Using Random Forests Guided by Shape Model

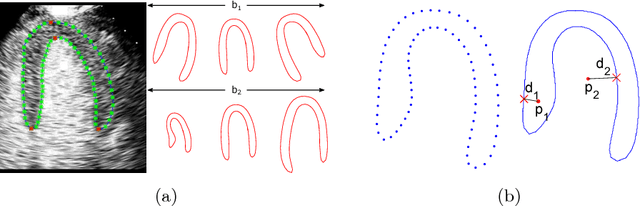
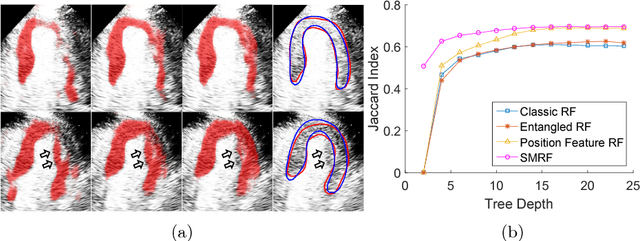
Myocardial Contrast Echocardiography (MCE) with micro-bubble contrast agent enables myocardial perfusion quantification which is invaluable for the early detection of coronary artery diseases. In this paper, we proposed a new segmentation method called Shape Model guided Random Forests (SMRF) for the analysis of MCE data. The proposed method utilizes a statistical shape model of the myocardium to guide the Random Forest (RF) segmentation in two ways. First, we introduce a novel Shape Model (SM) feature which captures the global structure and shape of the myocardium to produce a more accurate RF probability map. Second, the shape model is fitted to the RF probability map to further refine and constrain the final segmentation to plausible myocardial shapes. Evaluated on clinical MCE images from 15 patients, our method obtained promising results (Dice=0.81, Jaccard=0.70, MAD=1.68 mm, HD=6.53 mm) and showed a notable improvement in segmentation accuracy over the classic RF and its variants.