A Robust Anchor-based Method for Multi-Camera Pedestrian Localization

This paper addresses the problem of vision-based pedestrian localization, which estimates a pedestrian's location using images and camera parameters. In practice, however, calibrated camera parameters often deviate from the ground truth, leading to inaccuracies in localization. To address this issue, we propose an anchor-based method that leverages fixed-position anchors to reduce the impact of camera parameter errors. We provide a theoretical analysis that demonstrates the robustness of our approach. Experiments conducted on simulated, real-world, and public datasets show that our method significantly improves localization accuracy and remains resilient to noise in camera parameters, compared to methods without anchors.

Symmetric Matrix Completion with ReLU Sampling

We study the problem of symmetric positive semi-definite low-rank matrix completion (MC) with deterministic entry-dependent sampling. In particular, we consider rectified linear unit (ReLU) sampling, where only positive entries are observed, as well as a generalization to threshold-based sampling. We first empirically demonstrate that the landscape of this MC problem is not globally benign: Gradient descent (GD) with random initialization will generally converge to stationary points that are not globally optimal. Nevertheless, we prove that when the matrix factor with a small rank satisfies mild assumptions, the nonconvex objective function is geodesically strongly convex on the quotient manifold in a neighborhood of a planted low-rank matrix. Moreover, we show that our assumptions are satisfied by a matrix factor with i.i.d. Gaussian entries. Finally, we develop a tailor-designed initialization for GD to solve our studied formulation, which empirically always achieves convergence to the global minima. We also conduct extensive experiments and compare MC methods, investigating convergence and completion performance with respect to initialization, noise level, dimension, and rank.

A Global Geometric Analysis of Maximal Coding Rate Reduction

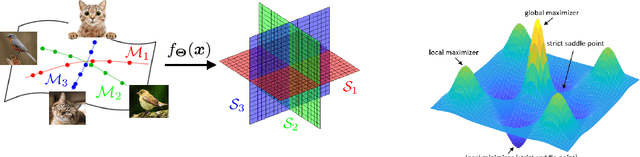
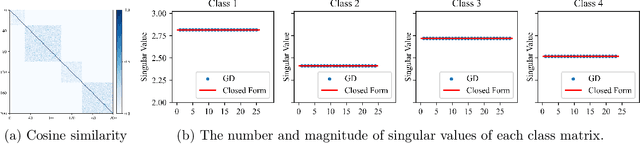
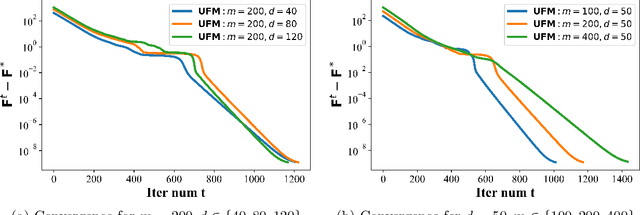
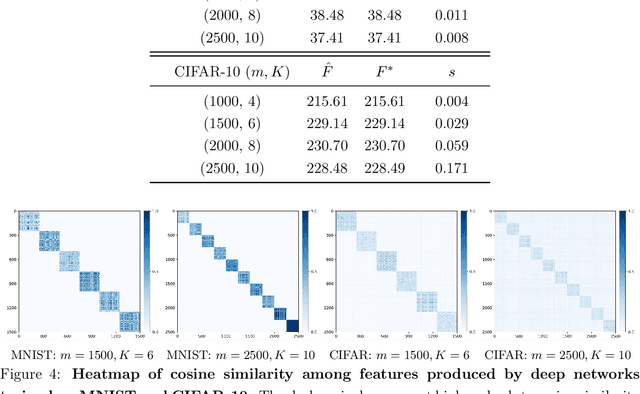
The maximal coding rate reduction (MCR$^2$) objective for learning structured and compact deep representations is drawing increasing attention, especially after its recent usage in the derivation of fully explainable and highly effective deep network architectures. However, it lacks a complete theoretical justification: only the properties of its global optima are known, and its global landscape has not been studied. In this work, we give a complete characterization of the properties of all its local and global optima, as well as other types of critical points. Specifically, we show that each (local or global) maximizer of the MCR$^2$ problem corresponds to a low-dimensional, discriminative, and diverse representation, and furthermore, each critical point of the objective is either a local maximizer or a strict saddle point. Such a favorable landscape makes MCR$^2$ a natural choice of objective for learning diverse and discriminative representations via first-order optimization methods. To validate our theoretical findings, we conduct extensive experiments on both synthetic and real data sets.

On the Estimation Performance of Generalized Power Method for Heteroscedastic Probabilistic PCA

The heteroscedastic probabilistic principal component analysis (PCA) technique, a variant of the classic PCA that considers data heterogeneity, is receiving more and more attention in the data science and signal processing communities. In this paper, to estimate the underlying low-dimensional linear subspace (simply called \emph{ground truth}) from available heterogeneous data samples, we consider the associated non-convex maximum-likelihood estimation problem, which involves maximizing a sum of heterogeneous quadratic forms over an orthogonality constraint (HQPOC). We propose a first-order method -- generalized power method (GPM) -- to tackle the problem and establish its \emph{estimation performance} guarantee. Specifically, we show that, given a suitable initialization, the distances between the iterates generated by GPM and the ground truth decrease at least geometrically to some threshold associated with the residual part of certain "population-residual decomposition". In establishing the estimation performance result, we prove a novel local error bound property of another closely related optimization problem, namely quadratic optimization with orthogonality constraint (QPOC), which is new and can be of independent interest. Numerical experiments are conducted to demonstrate the superior performance of GPM in both Gaussian noise and sub-Gaussian noise settings.

ReSync: Riemannian Subgradient-based Robust Rotation Synchronization

This work presents ReSync, a Riemannian subgradient-based algorithm for solving the robust rotation synchronization problem, which arises in various engineering applications. ReSync solves a least-unsquared minimization formulation over the rotation group, which is nonsmooth and nonconvex, and aims at recovering the underlying rotations directly. We provide strong theoretical guarantees for ReSync under the random corruption setting. Specifically, we first show that the initialization procedure of ReSync yields a proper initial point that lies in a local region around the ground-truth rotations. We next establish the weak sharpness property of the aforementioned formulation and then utilize this property to derive the local linear convergence of ReSync to the ground-truth rotations. By combining these guarantees, we conclude that ReSync converges linearly to the ground-truth rotations under appropriate conditions. Experiment results demonstrate the effectiveness of ReSync.

Differential Privacy via Distributionally Robust Optimization

In recent years, differential privacy has emerged as the de facto standard for sharing statistics of datasets while limiting the disclosure of private information about the involved individuals. This is achieved by randomly perturbing the statistics to be published, which in turn leads to a privacy-accuracy trade-off: larger perturbations provide stronger privacy guarantees, but they result in less accurate statistics that offer lower utility to the recipients. Of particular interest are therefore optimal mechanisms that provide the highest accuracy for a pre-selected level of privacy. To date, work in this area has focused on specifying families of perturbations a priori and subsequently proving their asymptotic and/or best-in-class optimality. In this paper, we develop a class of mechanisms that enjoy non-asymptotic and unconditional optimality guarantees. To this end, we formulate the mechanism design problem as an infinite-dimensional distributionally robust optimization problem. We show that the problem affords a strong dual, and we exploit this duality to develop converging hierarchies of finite-dimensional upper and lower bounding problems. Our upper (primal) bounds correspond to implementable perturbations whose suboptimality can be bounded by our lower (dual) bounds. Both bounding problems can be solved within seconds via cutting plane techniques that exploit the inherent problem structure. Our numerical experiments demonstrate that our perturbations can outperform the previously best results from the literature on artificial as well as standard benchmark problems.

A Convergent Single-Loop Algorithm for Relaxation of Gromov-Wasserstein in Graph Data

In this work, we present the Bregman Alternating Projected Gradient (BAPG) method, a single-loop algorithm that offers an approximate solution to the Gromov-Wasserstein (GW) distance. We introduce a novel relaxation technique that balances accuracy and computational efficiency, albeit with some compromises in the feasibility of the coupling map. Our analysis is based on the observation that the GW problem satisfies the Luo-Tseng error bound condition, which relates to estimating the distance of a point to the critical point set of the GW problem based on the optimality residual. This observation allows us to provide an approximation bound for the distance between the fixed-point set of BAPG and the critical point set of GW. Moreover, under a mild technical assumption, we can show that BAPG converges to its fixed point set. The effectiveness of BAPG has been validated through comprehensive numerical experiments in graph alignment and partition tasks, where it outperforms existing methods in terms of both solution quality and wall-clock time.

Convergence and Recovery Guarantees of the K-Subspaces Method for Subspace Clustering

The K-subspaces (KSS) method is a generalization of the K-means method for subspace clustering. In this work, we present local convergence analysis and a recovery guarantee for KSS, assuming data are generated by the semi-random union of subspaces model, where $N$ points are randomly sampled from $K \ge 2$ overlapping subspaces. We show that if the initial assignment of the KSS method lies within a neighborhood of a true clustering, it converges at a superlinear rate and finds the correct clustering within $\Theta(\log\log N)$ iterations with high probability. Moreover, we propose a thresholding inner-product based spectral method for initialization and prove that it produces a point in this neighborhood. We also present numerical results of the studied method to support our theoretical developments.

Fast and Provably Convergent Algorithms for Gromov-Wasserstein in Graph Learning

In this paper, we study the design and analysis of a class of efficient algorithms for computing the Gromov-Wasserstein (GW) distance tailored to large-scale graph learning tasks. Armed with the Luo-Tseng error bound condition~\cite{luo1992error}, two proposed algorithms, called Bregman Alternating Projected Gradient (BAPG) and hybrid Bregman Proximal Gradient (hBPG) are proven to be (linearly) convergent. Upon task-specific properties, our analysis further provides novel theoretical insights to guide how to select the best fit method. As a result, we are able to provide comprehensive experiments to validate the effectiveness of our methods on a host of tasks, including graph alignment, graph partition, and shape matching. In terms of both wall-clock time and modeling performance, the proposed methods achieve state-of-the-art results.

A Unified Approach to Synchronization Problems over Subgroups of the Orthogonal Group

Given a group $\mathcal{G}$, the problem of synchronization over the group $\mathcal{G}$ is a constrained estimation problem where a collection of group elements $G^*_1, \dots, G^*_n \in \mathcal{G}$ are estimated based on noisy observations of pairwise ratios $G^*_i {G^*_j}^{-1}$ for an incomplete set of index pairs $(i,j)$. This problem has gained much attention recently and finds lots of applications due to its appearance in a wide range of scientific and engineering areas. In this paper, we consider the class of synchronization problems over a closed subgroup of the orthogonal group, which covers many instances of group synchronization problems that arise in practice. Our contributions are threefold. First, we propose a unified approach to solve this class of group synchronization problems, which consists of a suitable initialization and an iterative refinement procedure via the generalized power method. Second, we derive a master theorem on the performance guarantee of the proposed approach. Under certain conditions on the subgroup, the measurement model, the noise model and the initialization, the estimation error of the iterates of our approach decreases geometrically. As our third contribution, we study concrete examples of the subgroup (including the orthogonal group, the special orthogonal group, the permutation group and the cyclic group), the measurement model, the noise model and the initialization. The validity of the related conditions in the master theorem are proved for these specific examples. Numerical experiments are also presented. Experiment results show that our approach outperforms existing approaches in terms of computational speed, scalability and estimation error.