A Global Geometric Analysis of Maximal Coding Rate Reduction
Paper and Code
Jun 04, 2024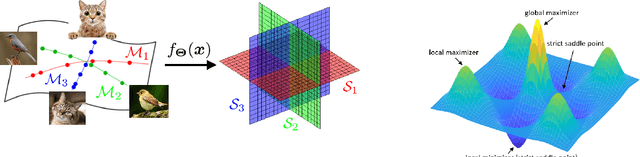
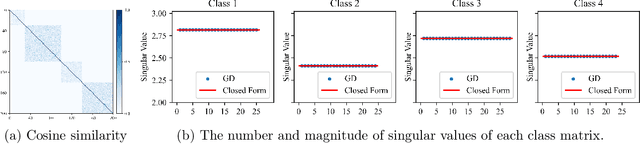
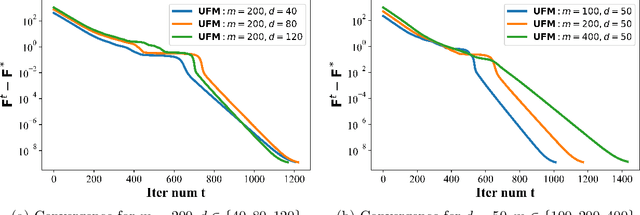
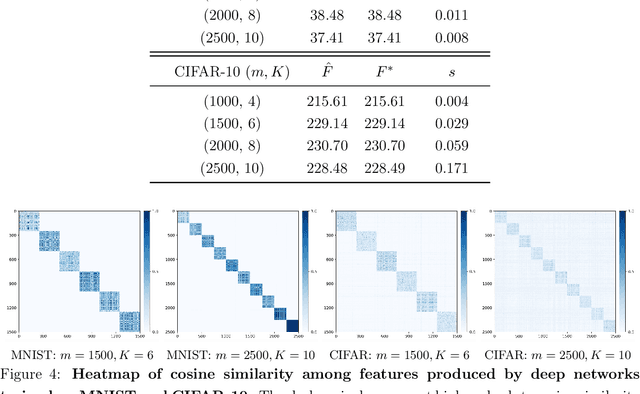
The maximal coding rate reduction (MCR$^2$) objective for learning structured and compact deep representations is drawing increasing attention, especially after its recent usage in the derivation of fully explainable and highly effective deep network architectures. However, it lacks a complete theoretical justification: only the properties of its global optima are known, and its global landscape has not been studied. In this work, we give a complete characterization of the properties of all its local and global optima, as well as other types of critical points. Specifically, we show that each (local or global) maximizer of the MCR$^2$ problem corresponds to a low-dimensional, discriminative, and diverse representation, and furthermore, each critical point of the objective is either a local maximizer or a strict saddle point. Such a favorable landscape makes MCR$^2$ a natural choice of objective for learning diverse and discriminative representations via first-order optimization methods. To validate our theoretical findings, we conduct extensive experiments on both synthetic and real data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge