Weighted Spectral Filters for Kernel Interpolation on Spheres: Estimates of Prediction Accuracy for Noisy Data

Spherical radial-basis-based kernel interpolation abounds in image sciences including geophysical image reconstruction, climate trends description and image rendering due to its excellent spatial localization property and perfect approximation performance. However, in dealing with noisy data, kernel interpolation frequently behaves not so well due to the large condition number of the kernel matrix and instability of the interpolation process. In this paper, we introduce a weighted spectral filter approach to reduce the condition number of the kernel matrix and then stabilize kernel interpolation. The main building blocks of the proposed method are the well developed spherical positive quadrature rules and high-pass spectral filters. Using a recently developed integral operator approach for spherical data analysis, we theoretically demonstrate that the proposed weighted spectral filter approach succeeds in breaking through the bottleneck of kernel interpolation, especially in fitting noisy data. We provide optimal approximation rates of the new method to show that our approach does not compromise the predicting accuracy. Furthermore, we conduct both toy simulations and two real-world data experiments with synthetically added noise in geophysical image reconstruction and climate image processing to verify our theoretical assertions and show the feasibility of the weighted spectral filter approach.

On the Estimation Performance of Generalized Power Method for Heteroscedastic Probabilistic PCA

The heteroscedastic probabilistic principal component analysis (PCA) technique, a variant of the classic PCA that considers data heterogeneity, is receiving more and more attention in the data science and signal processing communities. In this paper, to estimate the underlying low-dimensional linear subspace (simply called \emph{ground truth}) from available heterogeneous data samples, we consider the associated non-convex maximum-likelihood estimation problem, which involves maximizing a sum of heterogeneous quadratic forms over an orthogonality constraint (HQPOC). We propose a first-order method -- generalized power method (GPM) -- to tackle the problem and establish its \emph{estimation performance} guarantee. Specifically, we show that, given a suitable initialization, the distances between the iterates generated by GPM and the ground truth decrease at least geometrically to some threshold associated with the residual part of certain "population-residual decomposition". In establishing the estimation performance result, we prove a novel local error bound property of another closely related optimization problem, namely quadratic optimization with orthogonality constraint (QPOC), which is new and can be of independent interest. Numerical experiments are conducted to demonstrate the superior performance of GPM in both Gaussian noise and sub-Gaussian noise settings.

Decentralized Weakly Convex Optimization Over the Stiefel Manifold

We focus on a class of non-smooth optimization problems over the Stiefel manifold in the decentralized setting, where a connected network of $n$ agents cooperatively minimize a finite-sum objective function with each component being weakly convex in the ambient Euclidean space. Such optimization problems, albeit frequently encountered in applications, are quite challenging due to their non-smoothness and non-convexity. To tackle them, we propose an iterative method called the decentralized Riemannian subgradient method (DRSM). The global convergence and an iteration complexity of $\mathcal{O}(\varepsilon^{-2} \log^2(\varepsilon^{-1}))$ for forcing a natural stationarity measure below $\varepsilon$ are established via the powerful tool of proximal smoothness from variational analysis, which could be of independent interest. Besides, we show the local linear convergence of the DRSM using geometrically diminishing stepsizes when the problem at hand further possesses a sharpness property. Numerical experiments are conducted to corroborate our theoretical findings.

Orthogonal Group Synchronization with Incomplete Measurements: Error Bounds and Linear Convergence of the Generalized Power Method

Group synchronization refers to estimating a collection of group elements from the noisy pairwise measurements. Such a nonconvex problem has received much attention from numerous scientific fields including computer vision, robotics, and cryo-electron microscopy. In this paper, we focus on the orthogonal group synchronization problem with general additive noise models under incomplete measurements, which is much more general than the commonly considered setting of complete measurements. Characterizations of the orthogonal group synchronization problem are given from perspectives of optimality conditions as well as fixed points of the projected gradient ascent method which is also known as the generalized power method (GPM). It is well worth noting that these results still hold even without generative models. In the meantime, we derive the local error bound property for the orthogonal group synchronization problem which is useful for the convergence rate analysis of different algorithms and can be of independent interest. Finally, we prove the linear convergence result of the GPM to a global maximizer under a general additive noise model based on the established local error bound property. Our theoretical convergence result holds under several deterministic conditions which can cover certain cases with adversarial noise, and as an example we specialize it to the setting of the Erd\"os-R\'enyi measurement graph and Gaussian noise.

SHAQ: Incorporating Shapley Value Theory into Q-Learning for Multi-Agent Reinforcement Learning

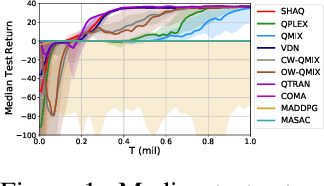
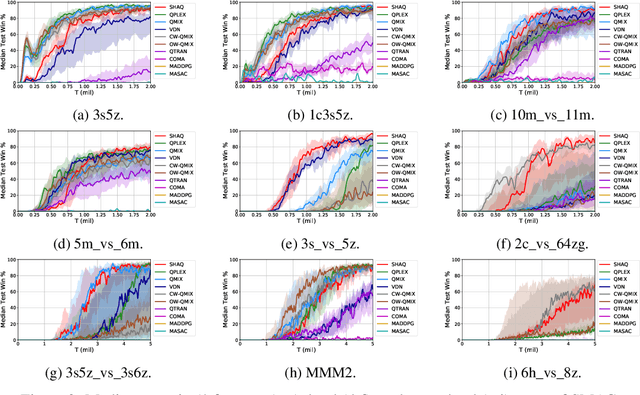
Value factorisation proves to be a very useful technique in multi-agent reinforcement learning (MARL), but the underlying mechanism is not yet fully understood. This paper explores a theoretic basis for value factorisation. We generalise the Shapley value in the coalitional game theory to a Markov convex game (MCG) and use it to guide value factorisation in MARL. We show that the generalised Shapley value possesses several features such as (1) accurate estimation of the maximum global value, (2) fairness in the factorisation of the global value, and (3) being sensitive to dummy agents. The proposed theory yields a new learning algorithm called Sharpley Q-learning (SHAQ), which inherits the important merits of ordinary Q-learning but extends it to MARL. In comparison with prior-arts, SHAQ has a much weaker assumption (MCG) that is more compatible with real-world problems, but has superior explainability and performance in many cases. We demonstrated SHAQ and verified the theoretic claims on Predator-Prey and StarCraft Multi-Agent Challenge (SMAC).