Boosting Gradient Ascent for Continuous DR-submodular Maximization

Projected Gradient Ascent (PGA) is the most commonly used optimization scheme in machine learning and operations research areas. Nevertheless, numerous studies and examples have shown that the PGA methods may fail to achieve the tight approximation ratio for continuous DR-submodular maximization problems. To address this challenge, we present a boosting technique in this paper, which can efficiently improve the approximation guarantee of the standard PGA to \emph{optimal} with only small modifications on the objective function. The fundamental idea of our boosting technique is to exploit non-oblivious search to derive a novel auxiliary function $F$, whose stationary points are excellent approximations to the global maximum of the original DR-submodular objective $f$. Specifically, when $f$ is monotone and $\gamma$-weakly DR-submodular, we propose an auxiliary function $F$ whose stationary points can provide a better $(1-e^{-\gamma})$-approximation than the $(\gamma^2/(1+\gamma^2))$-approximation guaranteed by the stationary points of $f$ itself. Similarly, for the non-monotone case, we devise another auxiliary function $F$ whose stationary points can achieve an optimal $\frac{1-\min_{\boldsymbol{x}\in\mathcal{C}}\|\boldsymbol{x}\|_{\infty}}{4}$-approximation guarantee where $\mathcal{C}$ is a convex constraint set. In contrast, the stationary points of the original non-monotone DR-submodular function can be arbitrarily bad~\citep{chen2023continuous}. Furthermore, we demonstrate the scalability of our boosting technique on four problems. In all of these four problems, our resulting variants of boosting PGA algorithm beat the previous standard PGA in several aspects such as approximation ratio and efficiency. Finally, we corroborate our theoretical findings with numerical experiments, which demonstrate the effectiveness of our boosting PGA methods.

Multi-channel Integrated Recommendation with Exposure Constraints

Integrated recommendation, which aims at jointly recommending heterogeneous items from different channels in a main feed, has been widely applied to various online platforms. Though attractive, integrated recommendation requires the ranking methods to migrate from conventional user-item models to the new user-channel-item paradigm in order to better capture users' preferences on both item and channel levels. Moreover, practical feed recommendation systems usually impose exposure constraints on different channels to ensure user experience. This leads to greater difficulty in the joint ranking of heterogeneous items. In this paper, we investigate the integrated recommendation task with exposure constraints in practical recommender systems. Our contribution is forth-fold. First, we formulate this task as a binary online linear programming problem and propose a two-layer framework named Multi-channel Integrated Recommendation with Exposure Constraints (MIREC) to obtain the optimal solution. Second, we propose an efficient online allocation algorithm to determine the optimal exposure assignment of different channels from a global view of all user requests over the entire time horizon. We prove that this algorithm reaches the optimal point under a regret bound of $ \mathcal{O}(\sqrt{T}) $ with linear complexity. Third, we propose a series of collaborative models to determine the optimal layout of heterogeneous items at each user request. The joint modeling of user interests, cross-channel correlation, and page context in our models aligns more with the browsing nature of feed products than existing models. Finally, we conduct extensive experiments on both offline datasets and online A/B tests to verify the effectiveness of MIREC. The proposed framework has now been implemented on the homepage of Taobao to serve the main traffic.

Decentralized Weakly Convex Optimization Over the Stiefel Manifold

We focus on a class of non-smooth optimization problems over the Stiefel manifold in the decentralized setting, where a connected network of $n$ agents cooperatively minimize a finite-sum objective function with each component being weakly convex in the ambient Euclidean space. Such optimization problems, albeit frequently encountered in applications, are quite challenging due to their non-smoothness and non-convexity. To tackle them, we propose an iterative method called the decentralized Riemannian subgradient method (DRSM). The global convergence and an iteration complexity of $\mathcal{O}(\varepsilon^{-2} \log^2(\varepsilon^{-1}))$ for forcing a natural stationarity measure below $\varepsilon$ are established via the powerful tool of proximal smoothness from variational analysis, which could be of independent interest. Besides, we show the local linear convergence of the DRSM using geometrically diminishing stepsizes when the problem at hand further possesses a sharpness property. Numerical experiments are conducted to corroborate our theoretical findings.

An Online Algorithm for Chance Constrained Resource Allocation

This paper studies the online stochastic resource allocation problem (RAP) with chance constraints. The online RAP is a 0-1 integer linear programming problem where the resource consumption coefficients are revealed column by column along with the corresponding revenue coefficients. When a column is revealed, the corresponding decision variables are determined instantaneously without future information. Moreover, in online applications, the resource consumption coefficients are often obtained by prediction. To model their uncertainties, we take the chance constraints into the consideration. To the best of our knowledge, this is the first time chance constraints are introduced in the online RAP problem. Assuming that the uncertain variables have known Gaussian distributions, the stochastic RAP can be transformed into a deterministic but nonlinear problem with integer second-order cone constraints. Next, we linearize this nonlinear problem and analyze the performance of vanilla online primal-dual algorithm for solving the linearized stochastic RAP. Under mild technical assumptions, the optimality gap and constraint violation are both on the order of $\sqrt{n}$. Then, to further improve the performance of the algorithm, several modified online primal-dual algorithms with heuristic corrections are proposed. Finally, extensive numerical experiments on both synthetic and real data demonstrate the applicability and effectiveness of our methods.

Communication-Efficient Decentralized Online Continuous DR-Submodular Maximization

Maximizing a monotone submodular function is a fundamental task in machine learning, economics, and statistics. In this paper, we present two communication-efficient decentralized online algorithms for the monotone continuous DR-submodular maximization problem, both of which reduce the number of per-function gradient evaluations and per-round communication complexity from $T^{3/2}$ to $1$. The first one, One-shot Decentralized Meta-Frank-Wolfe (Mono-DMFW), achieves a $(1-1/e)$-regret bound of $O(T^{4/5})$. As far as we know, this is the first one-shot and projection-free decentralized online algorithm for monotone continuous DR-submodular maximization. Next, inspired by the non-oblivious boosting function \citep{zhang2022boosting}, we propose the Decentralized Online Boosting Gradient Ascent (DOBGA) algorithm, which attains a $(1-1/e)$-regret of $O(\sqrt{T})$. To the best of our knowledge, this is the first result to obtain the optimal $O(\sqrt{T})$ against a $(1-1/e)$-approximation with only one gradient inquiry for each local objective function per step. Finally, various experimental results confirm the effectiveness of the proposed methods.

Online Learning for Non-monotone Submodular Maximization: From Full Information to Bandit Feedback

In this paper, we revisit the online non-monotone continuous DR-submodular maximization problem over a down-closed convex set, which finds wide real-world applications in the domain of machine learning, economics, and operations research. At first, we present the Meta-MFW algorithm achieving a $1/e$-regret of $O(\sqrt{T})$ at the cost of $T^{3/2}$ stochastic gradient evaluations per round. As far as we know, Meta-MFW is the first algorithm to obtain $1/e$-regret of $O(\sqrt{T})$ for the online non-monotone continuous DR-submodular maximization problem over a down-closed convex set. Furthermore, in sharp contrast with ODC algorithm \citep{thang2021online}, Meta-MFW relies on the simple online linear oracle without discretization, lifting, or rounding operations. Considering the practical restrictions, we then propose the Mono-MFW algorithm, which reduces the per-function stochastic gradient evaluations from $T^{3/2}$ to 1 and achieves a $1/e$-regret bound of $O(T^{4/5})$. Next, we extend Mono-MFW to the bandit setting and propose the Bandit-MFW algorithm which attains a $1/e$-regret bound of $O(T^{8/9})$. To the best of our knowledge, Mono-MFW and Bandit-MFW are the first sublinear-regret algorithms to explore the one-shot and bandit setting for online non-monotone continuous DR-submodular maximization problem over a down-closed convex set, respectively. Finally, we conduct numerical experiments on both synthetic and real-world datasets to verify the effectiveness of our methods.

Neighbor Enhanced Graph Convolutional Networks for Node Classification and Recommendation

The recently proposed Graph Convolutional Networks (GCNs) have achieved significantly superior performance on various graph-related tasks, such as node classification and recommendation. However, currently researches on GCN models usually recursively aggregate the information from all the neighbors or randomly sampled neighbor subsets, without explicitly identifying whether the aggregated neighbors provide useful information during the graph convolution. In this paper, we theoretically analyze the affection of the neighbor quality over GCN models' performance and propose the Neighbor Enhanced Graph Convolutional Network (NEGCN) framework to boost the performance of existing GCN models. Our contribution is three-fold. First, we at the first time propose the concept of neighbor quality for both node classification and recommendation tasks in a general theoretical framework. Specifically, for node classification, we propose three propositions to theoretically analyze how the neighbor quality affects the node classification performance of GCN models. Second, based on the three proposed propositions, we introduce the graph refinement process including specially designed neighbor evaluation methods to increase the neighbor quality so as to boost both the node classification and recommendation tasks. Third, we conduct extensive node classification and recommendation experiments on several benchmark datasets. The experimental results verify that our proposed NEGCN framework can significantly enhance the performance for various typical GCN models on both node classification and recommendation tasks.

Continuous Submodular Maximization: Boosting via Non-oblivious Function

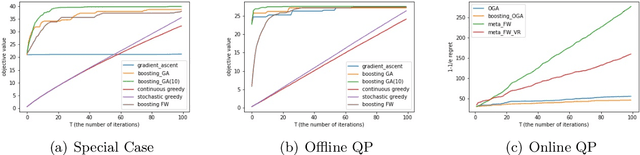
In this paper, we revisit the constrained and stochastic continuous submodular maximization in both offline and online settings. For each $\gamma$-weakly DR-submodular function $f$, we use the factor-revealing optimization equation to derive an optimal auxiliary function $F$, whose stationary points provide a $(1-e^{-\gamma})$-approximation to the global maximum value (denoted as $OPT$) of problem $\max_{\boldsymbol{x}\in\mathcal{C}}f(\boldsymbol{x})$. Naturally, the projected (mirror) gradient ascent relied on this non-oblivious function achieves $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{2})$ iterations, beating the traditional $(\frac{\gamma^{2}}{1+\gamma^{2}})$-approximation gradient ascent \citep{hassani2017gradient} for submodular maximization. Similarly, based on $F$, the classical Frank-Wolfe algorithm equipped with variance reduction technique \citep{mokhtari2018conditional} also returns a solution with objective value larger than $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{3})$ iterations. In the online setting, we first consider the adversarial delays for stochastic gradient feedback, under which we propose a boosting online gradient algorithm with the same non-oblivious search, achieving a regret of $\sqrt{D}$ (where $D$ is the sum of delays of gradient feedback) against a $(1-e^{-\gamma})$-approximation to the best feasible solution in hindsight. Finally, extensive numerical experiments demonstrate the efficiency of our boosting methods.

Non-Recursive Graph Convolutional Networks

Graph Convolutional Networks (GCNs) are powerful models for node representation learning tasks. However, the node representation in existing GCN models is usually generated by performing recursive neighborhood aggregation across multiple graph convolutional layers with certain sampling methods, which may lead to redundant feature mixing, needless information loss, and extensive computations. Therefore, in this paper, we propose a novel architecture named Non-Recursive Graph Convolutional Network (NRGCN) to improve both the training efficiency and the learning performance of GCNs in the context of node classification. Specifically, NRGCN proposes to represent different hops of neighbors for each node based on inner-layer aggregation and layer-independent sampling. In this way, each node can be directly represented by concatenating the information extracted independently from each hop of its neighbors thereby avoiding the recursive neighborhood expansion across layers. Moreover, the layer-independent sampling and aggregation can be precomputed before the model training, thus the training process can be accelerated considerably. Extensive experiments on benchmark datasets verify that our NRGCN outperforms the state-of-the-art GCN models, in terms of the node classification performance and reliability.

Single-Layer Graph Convolutional Networks For Recommendation

Graph Convolutional Networks (GCNs) and their variants have received significant attention and achieved start-of-the-art performances on various recommendation tasks. However, many existing GCN models tend to perform recursive aggregations among all related nodes, which arises severe computational burden. Moreover, they favor multi-layer architectures in conjunction with complicated modeling techniques. Though effective, the excessive amount of model parameters largely hinder their applications in real-world recommender systems. To this end, in this paper, we propose the single-layer GCN model which is able to achieve superior performance along with remarkably less complexity compared with existing models. Our main contribution is three-fold. First, we propose a principled similarity metric named distribution-aware similarity (DA similarity), which can guide the neighbor sampling process and evaluate the quality of the input graph explicitly. We also prove that DA similarity has a positive correlation with the final performance, through both theoretical analysis and empirical simulations. Second, we propose a simplified GCN architecture which employs a single GCN layer to aggregate information from the neighbors filtered by DA similarity and then generates the node representations. Moreover, the aggregation step is a parameter-free operation, such that it can be done in a pre-processing manner to further reduce red the training and inference costs. Third, we conduct extensive experiments on four datasets. The results verify that the proposed model outperforms existing GCN models considerably and yields up to a few orders of magnitude speedup in training, in terms of the recommendation performance.