Boosting Gradient Ascent for Continuous DR-submodular Maximization

Projected Gradient Ascent (PGA) is the most commonly used optimization scheme in machine learning and operations research areas. Nevertheless, numerous studies and examples have shown that the PGA methods may fail to achieve the tight approximation ratio for continuous DR-submodular maximization problems. To address this challenge, we present a boosting technique in this paper, which can efficiently improve the approximation guarantee of the standard PGA to \emph{optimal} with only small modifications on the objective function. The fundamental idea of our boosting technique is to exploit non-oblivious search to derive a novel auxiliary function $F$, whose stationary points are excellent approximations to the global maximum of the original DR-submodular objective $f$. Specifically, when $f$ is monotone and $\gamma$-weakly DR-submodular, we propose an auxiliary function $F$ whose stationary points can provide a better $(1-e^{-\gamma})$-approximation than the $(\gamma^2/(1+\gamma^2))$-approximation guaranteed by the stationary points of $f$ itself. Similarly, for the non-monotone case, we devise another auxiliary function $F$ whose stationary points can achieve an optimal $\frac{1-\min_{\boldsymbol{x}\in\mathcal{C}}\|\boldsymbol{x}\|_{\infty}}{4}$-approximation guarantee where $\mathcal{C}$ is a convex constraint set. In contrast, the stationary points of the original non-monotone DR-submodular function can be arbitrarily bad~\citep{chen2023continuous}. Furthermore, we demonstrate the scalability of our boosting technique on four problems. In all of these four problems, our resulting variants of boosting PGA algorithm beat the previous standard PGA in several aspects such as approximation ratio and efficiency. Finally, we corroborate our theoretical findings with numerical experiments, which demonstrate the effectiveness of our boosting PGA methods.

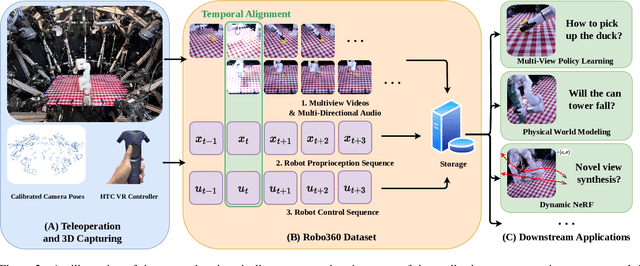
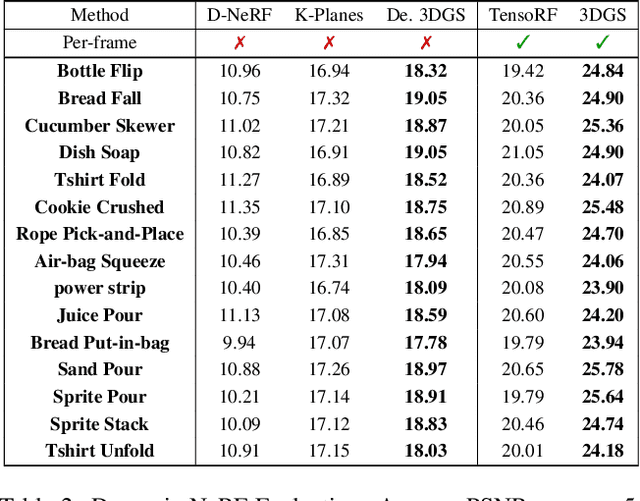
Robo360: A 3D Omnispective Multi-Material Robotic Manipulation Dataset

Building robots that can automate labor-intensive tasks has long been the core motivation behind the advancements in computer vision and the robotics community. Recent interest in leveraging 3D algorithms, particularly neural fields, has led to advancements in robot perception and physical understanding in manipulation scenarios. However, the real world's complexity poses significant challenges. To tackle these challenges, we present Robo360, a dataset that features robotic manipulation with a dense view coverage, which enables high-quality 3D neural representation learning, and a diverse set of objects with various physical and optical properties and facilitates research in various object manipulation and physical world modeling tasks. We confirm the effectiveness of our dataset using existing dynamic NeRF and evaluate its potential in learning multi-view policies. We hope that Robo360 can open new research directions yet to be explored at the intersection of understanding the physical world in 3D and robot control.

Towards A Robust Group-level Emotion Recognition via Uncertainty-Aware Learning

Group-level emotion recognition (GER) is an inseparable part of human behavior analysis, aiming to recognize an overall emotion in a multi-person scene. However, the existing methods are devoted to combing diverse emotion cues while ignoring the inherent uncertainties under unconstrained environments, such as congestion and occlusion occurring within a group. Additionally, since only group-level labels are available, inconsistent emotion predictions among individuals in one group can confuse the network. In this paper, we propose an uncertainty-aware learning (UAL) method to extract more robust representations for GER. By explicitly modeling the uncertainty of each individual, we utilize stochastic embedding drawn from a Gaussian distribution instead of deterministic point embedding. This representation captures the probabilities of different emotions and generates diverse predictions through this stochasticity during the inference stage. Furthermore, uncertainty-sensitive scores are adaptively assigned as the fusion weights of individuals' face within each group. Moreover, we develop an image enhancement module to enhance the model's robustness against severe noise. The overall three-branch model, encompassing face, object, and scene component, is guided by a proportional-weighted fusion strategy and integrates the proposed uncertainty-aware method to produce the final group-level output. Experimental results demonstrate the effectiveness and generalization ability of our method across three widely used databases.

Bandit Multi-linear DR-Submodular Maximization and Its Applications on Adversarial Submodular Bandits

We investigate the online bandit learning of the monotone multi-linear DR-submodular functions, designing the algorithm $\mathtt{BanditMLSM}$ that attains $O(T^{2/3}\log T)$ of $(1-1/e)$-regret. Then we reduce submodular bandit with partition matroid constraint and bandit sequential monotone maximization to the online bandit learning of the monotone multi-linear DR-submodular functions, attaining $O(T^{2/3}\log T)$ of $(1-1/e)$-regret in both problems, which improve the existing results. To the best of our knowledge, we are the first to give a sublinear regret algorithm for the submodular bandit with partition matroid constraint. A special case of this problem is studied by Streeter et al.(2009). They prove a $O(T^{4/5})$ $(1-1/e)$-regret upper bound. For the bandit sequential submodular maximization, the existing work proves an $O(T^{2/3})$ regret with a suboptimal $1/2$ approximation ratio (Niazadeh et al. 2021).

Reparameterization through Spatial Gradient Scaling

Reparameterization aims to improve the generalization of deep neural networks by transforming convolutional layers into equivalent multi-branched structures during training. However, there exists a gap in understanding how reparameterization may change and benefit the learning process of neural networks. In this paper, we present a novel spatial gradient scaling method to redistribute learning focus among weights in convolutional networks. We prove that spatial gradient scaling achieves the same learning dynamics as a branched reparameterization yet without introducing structural changes into the network. We further propose an analytical approach that dynamically learns scalings for each convolutional layer based on the spatial characteristics of its input feature map gauged by mutual information. Experiments on CIFAR-10, CIFAR-100, and ImageNet show that without searching for reparameterized structures, our proposed scaling method outperforms the state-of-the-art reparameterization strategies at a lower computational cost.

A General-Purpose Transferable Predictor for Neural Architecture Search

Understanding and modelling the performance of neural architectures is key to Neural Architecture Search (NAS). Performance predictors have seen widespread use in low-cost NAS and achieve high ranking correlations between predicted and ground truth performance in several NAS benchmarks. However, existing predictors are often designed based on network encodings specific to a predefined search space and are therefore not generalizable to other search spaces or new architecture families. In this paper, we propose a general-purpose neural predictor for NAS that can transfer across search spaces, by representing any given candidate Convolutional Neural Network (CNN) with a Computation Graph (CG) that consists of primitive operators. We further combine our CG network representation with Contrastive Learning (CL) and propose a graph representation learning procedure that leverages the structural information of unlabeled architectures from multiple families to train CG embeddings for our performance predictor. Experimental results on NAS-Bench-101, 201 and 301 demonstrate the efficacy of our scheme as we achieve strong positive Spearman Rank Correlation Coefficient (SRCC) on every search space, outperforming several Zero-Cost Proxies, including Synflow and Jacov, which are also generalizable predictors across search spaces. Moreover, when using our proposed general-purpose predictor in an evolutionary neural architecture search algorithm, we can find high-performance architectures on NAS-Bench-101 and find a MobileNetV3 architecture that attains 79.2% top-1 accuracy on ImageNet.

GENNAPE: Towards Generalized Neural Architecture Performance Estimators

Predicting neural architecture performance is a challenging task and is crucial to neural architecture design and search. Existing approaches either rely on neural performance predictors which are limited to modeling architectures in a predefined design space involving specific sets of operators and connection rules, and cannot generalize to unseen architectures, or resort to zero-cost proxies which are not always accurate. In this paper, we propose GENNAPE, a Generalized Neural Architecture Performance Estimator, which is pretrained on open neural architecture benchmarks, and aims to generalize to completely unseen architectures through combined innovations in network representation, contrastive pretraining, and fuzzy clustering-based predictor ensemble. Specifically, GENNAPE represents a given neural network as a Computation Graph (CG) of atomic operations which can model an arbitrary architecture. It first learns a graph encoder via Contrastive Learning to encourage network separation by topological features, and then trains multiple predictor heads, which are soft-aggregated according to the fuzzy membership of a neural network. Experiments show that GENNAPE pretrained on NAS-Bench-101 can achieve superior transferability to 5 different public neural network benchmarks, including NAS-Bench-201, NAS-Bench-301, MobileNet and ResNet families under no or minimum fine-tuning. We further introduce 3 challenging newly labelled neural network benchmarks: HiAML, Inception and Two-Path, which can concentrate in narrow accuracy ranges. Extensive experiments show that GENNAPE can correctly discern high-performance architectures in these families. Finally, when paired with a search algorithm, GENNAPE can find architectures that improve accuracy while reducing FLOPs on three families.

AIO-P: Expanding Neural Performance Predictors Beyond Image Classification

Evaluating neural network performance is critical to deep neural network design but a costly procedure. Neural predictors provide an efficient solution by treating architectures as samples and learning to estimate their performance on a given task. However, existing predictors are task-dependent, predominantly estimating neural network performance on image classification benchmarks. They are also search-space dependent; each predictor is designed to make predictions for a specific architecture search space with predefined topologies and set of operations. In this paper, we propose a novel All-in-One Predictor (AIO-P), which aims to pretrain neural predictors on architecture examples from multiple, separate computer vision (CV) task domains and multiple architecture spaces, and then transfer to unseen downstream CV tasks or neural architectures. We describe our proposed techniques for general graph representation, efficient predictor pretraining and knowledge infusion techniques, as well as methods to transfer to downstream tasks/spaces. Extensive experimental results show that AIO-P can achieve Mean Absolute Error (MAE) and Spearman's Rank Correlation (SRCC) below 1% and above 0.5, respectively, on a breadth of target downstream CV tasks with or without fine-tuning, outperforming a number of baselines. Moreover, AIO-P can directly transfer to new architectures not seen during training, accurately rank them and serve as an effective performance estimator when paired with an algorithm designed to preserve performance while reducing FLOPs.

Quantum Multi-Armed Bandits and Stochastic Linear Bandits Enjoy Logarithmic Regrets

Multi-arm bandit (MAB) and stochastic linear bandit (SLB) are important models in reinforcement learning, and it is well-known that classical algorithms for bandits with time horizon $T$ suffer $\Omega(\sqrt{T})$ regret. In this paper, we study MAB and SLB with quantum reward oracles and propose quantum algorithms for both models with $O(\mbox{poly}(\log T))$ regrets, exponentially improving the dependence in terms of $T$. To the best of our knowledge, this is the first provable quantum speedup for regrets of bandit problems and in general exploitation in reinforcement learning. Compared to previous literature on quantum exploration algorithms for MAB and reinforcement learning, our quantum input model is simpler and only assumes quantum oracles for each individual arm.

Bounded Memory Adversarial Bandits with Composite Anonymous Delayed Feedback

We study the adversarial bandit problem with composite anonymous delayed feedback. In this setting, losses of an action are split into $d$ components, spreading over consecutive rounds after the action is chosen. And in each round, the algorithm observes the aggregation of losses that come from the latest $d$ rounds. Previous works focus on oblivious adversarial setting, while we investigate the harder non-oblivious setting. We show non-oblivious setting incurs $\Omega(T)$ pseudo regret even when the loss sequence is bounded memory. However, we propose a wrapper algorithm which enjoys $o(T)$ policy regret on many adversarial bandit problems with the assumption that the loss sequence is bounded memory. Especially, for $K$-armed bandit and bandit convex optimization, we have $\mathcal{O}(T^{2/3})$ policy regret bound. We also prove a matching lower bound for $K$-armed bandit. Our lower bound works even when the loss sequence is oblivious but the delay is non-oblivious. It answers the open problem proposed in \cite{wang2021adaptive}, showing that non-oblivious delay is enough to incur $\tilde{\Omega}(T^{2/3})$ regret.