GraphOmni: A Comprehensive and Extendable Benchmark Framework for Large Language Models on Graph-theoretic Tasks

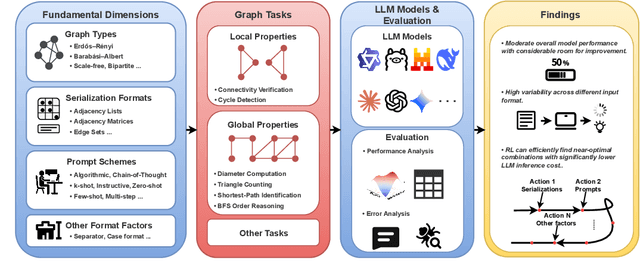
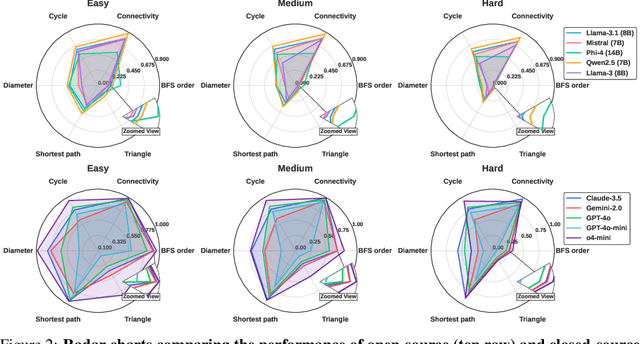
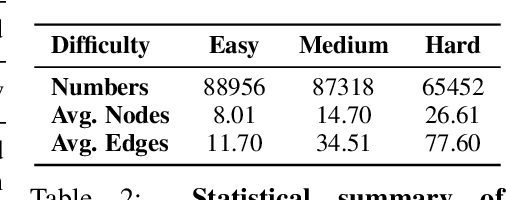
In this paper, we presented GraphOmni, a comprehensive benchmark framework for systematically evaluating the graph reasoning capabilities of LLMs. By analyzing critical dimensions, including graph types, serialization formats, and prompt schemes, we provided extensive insights into the strengths and limitations of current LLMs. Our empirical findings emphasize that no single serialization or prompting strategy consistently outperforms others. Motivated by these insights, we propose a reinforcement learning-based approach that dynamically selects the best serialization-prompt pairings, resulting in significant accuracy improvements. GraphOmni's modular and extensible design establishes a robust foundation for future research, facilitating advancements toward general-purpose graph reasoning models.

Two Heads are Better Than One: Test-time Scaling of Multi-agent Collaborative Reasoning

Multi-agent systems (MAS) built on large language models (LLMs) offer a promising path toward solving complex, real-world tasks that single-agent systems often struggle to manage. While recent advancements in test-time scaling (TTS) have significantly improved single-agent performance on challenging reasoning tasks, how to effectively scale collaboration and reasoning in MAS remains an open question. In this work, we introduce an adaptive multi-agent framework designed to enhance collaborative reasoning through both model-level training and system-level coordination. We construct M500, a high-quality dataset containing 500 multi-agent collaborative reasoning traces, and fine-tune Qwen2.5-32B-Instruct on this dataset to produce M1-32B, a model optimized for multi-agent collaboration. To further enable adaptive reasoning, we propose a novel CEO agent that dynamically manages the discussion process, guiding agent collaboration and adjusting reasoning depth for more effective problem-solving. Evaluated in an open-source MAS across a range of tasks-including general understanding, mathematical reasoning, and coding-our system significantly outperforms strong baselines. For instance, M1-32B achieves 12% improvement on GPQA-Diamond, 41% on AIME2024, and 10% on MBPP-Sanitized, matching the performance of state-of-the-art models like DeepSeek-R1 on some tasks. These results highlight the importance of both learned collaboration and adaptive coordination in scaling multi-agent reasoning. Code is available at https://github.com/jincan333/MAS-TTS

Near-Optimal Online Learning for Multi-Agent Submodular Coordination: Tight Approximation and Communication Efficiency

Coordinating multiple agents to collaboratively maximize submodular functions in unpredictable environments is a critical task with numerous applications in machine learning, robot planning and control. The existing approaches, such as the OSG algorithm, are often hindered by their poor approximation guarantees and the rigid requirement for a fully connected communication graph. To address these challenges, we firstly present a $\textbf{MA-OSMA}$ algorithm, which employs the multi-linear extension to transfer the discrete submodular maximization problem into a continuous optimization, thereby allowing us to reduce the strict dependence on a complete graph through consensus techniques. Moreover, $\textbf{MA-OSMA}$ leverages a novel surrogate gradient to avoid sub-optimal stationary points. To eliminate the computationally intensive projection operations in $\textbf{MA-OSMA}$, we also introduce a projection-free $\textbf{MA-OSEA}$ algorithm, which effectively utilizes the KL divergence by mixing a uniform distribution. Theoretically, we confirm that both algorithms achieve a regret bound of $\widetilde{O}(\sqrt{\frac{C_{T}T}{1-\beta}})$ against a $(\frac{1-e^{-c}}{c})$-approximation to the best comparator in hindsight, where $C_{T}$ is the deviation of maximizer sequence, $\beta$ is the spectral gap of the network and $c$ is the joint curvature of submodular objectives. This result significantly improves the $(\frac{1}{1+c})$-approximation provided by the state-of-the-art OSG algorithm. Finally, we demonstrate the effectiveness of our proposed algorithms through simulation-based multi-target tracking.

Refining Adaptive Zeroth-Order Optimization at Ease

Recently, zeroth-order (ZO) optimization plays an essential role in scenarios where gradient information is inaccessible or unaffordable, such as black-box systems and resource-constrained environments. While existing adaptive methods such as ZO-AdaMM have shown promise, they are fundamentally limited by their underutilization of moment information during optimization, usually resulting in underperforming convergence. To overcome these limitations, this paper introduces Refined Adaptive Zeroth-Order Optimization (R-AdaZO). Specifically, we first show the untapped variance reduction effect of first moment estimate on ZO gradient estimation, which improves the accuracy and stability of ZO updates. We then refine the second moment estimate based on these variance-reduced gradient estimates to better capture the geometry of the optimization landscape, enabling a more effective scaling of ZO updates. We present rigorous theoretical analysis to show (I) the first analysis to the variance reduction of first moment estimate in ZO optimization, (II) the improved second moment estimates with a more accurate approximation of its variance-free ideal, (III) the first variance-aware convergence framework for adaptive ZO methods, which may be of independent interest, and (IV) the faster convergence of R-AdaZO than existing baselines like ZO-AdaMM. Our extensive experiments, including synthetic problems, black-box adversarial attack, and memory-efficient fine-tuning of large language models (LLMs), further verify the superior convergence of R-AdaZO, indicating that R-AdaZO offers an improved solution for real-world ZO optimization challenges.

Boosting Gradient Ascent for Continuous DR-submodular Maximization

Projected Gradient Ascent (PGA) is the most commonly used optimization scheme in machine learning and operations research areas. Nevertheless, numerous studies and examples have shown that the PGA methods may fail to achieve the tight approximation ratio for continuous DR-submodular maximization problems. To address this challenge, we present a boosting technique in this paper, which can efficiently improve the approximation guarantee of the standard PGA to \emph{optimal} with only small modifications on the objective function. The fundamental idea of our boosting technique is to exploit non-oblivious search to derive a novel auxiliary function $F$, whose stationary points are excellent approximations to the global maximum of the original DR-submodular objective $f$. Specifically, when $f$ is monotone and $\gamma$-weakly DR-submodular, we propose an auxiliary function $F$ whose stationary points can provide a better $(1-e^{-\gamma})$-approximation than the $(\gamma^2/(1+\gamma^2))$-approximation guaranteed by the stationary points of $f$ itself. Similarly, for the non-monotone case, we devise another auxiliary function $F$ whose stationary points can achieve an optimal $\frac{1-\min_{\boldsymbol{x}\in\mathcal{C}}\|\boldsymbol{x}\|_{\infty}}{4}$-approximation guarantee where $\mathcal{C}$ is a convex constraint set. In contrast, the stationary points of the original non-monotone DR-submodular function can be arbitrarily bad~\citep{chen2023continuous}. Furthermore, we demonstrate the scalability of our boosting technique on four problems. In all of these four problems, our resulting variants of boosting PGA algorithm beat the previous standard PGA in several aspects such as approximation ratio and efficiency. Finally, we corroborate our theoretical findings with numerical experiments, which demonstrate the effectiveness of our boosting PGA methods.

Communication-Efficient Decentralized Online Continuous DR-Submodular Maximization

Maximizing a monotone submodular function is a fundamental task in machine learning, economics, and statistics. In this paper, we present two communication-efficient decentralized online algorithms for the monotone continuous DR-submodular maximization problem, both of which reduce the number of per-function gradient evaluations and per-round communication complexity from $T^{3/2}$ to $1$. The first one, One-shot Decentralized Meta-Frank-Wolfe (Mono-DMFW), achieves a $(1-1/e)$-regret bound of $O(T^{4/5})$. As far as we know, this is the first one-shot and projection-free decentralized online algorithm for monotone continuous DR-submodular maximization. Next, inspired by the non-oblivious boosting function \citep{zhang2022boosting}, we propose the Decentralized Online Boosting Gradient Ascent (DOBGA) algorithm, which attains a $(1-1/e)$-regret of $O(\sqrt{T})$. To the best of our knowledge, this is the first result to obtain the optimal $O(\sqrt{T})$ against a $(1-1/e)$-approximation with only one gradient inquiry for each local objective function per step. Finally, various experimental results confirm the effectiveness of the proposed methods.

Online Learning for Non-monotone Submodular Maximization: From Full Information to Bandit Feedback

In this paper, we revisit the online non-monotone continuous DR-submodular maximization problem over a down-closed convex set, which finds wide real-world applications in the domain of machine learning, economics, and operations research. At first, we present the Meta-MFW algorithm achieving a $1/e$-regret of $O(\sqrt{T})$ at the cost of $T^{3/2}$ stochastic gradient evaluations per round. As far as we know, Meta-MFW is the first algorithm to obtain $1/e$-regret of $O(\sqrt{T})$ for the online non-monotone continuous DR-submodular maximization problem over a down-closed convex set. Furthermore, in sharp contrast with ODC algorithm \citep{thang2021online}, Meta-MFW relies on the simple online linear oracle without discretization, lifting, or rounding operations. Considering the practical restrictions, we then propose the Mono-MFW algorithm, which reduces the per-function stochastic gradient evaluations from $T^{3/2}$ to 1 and achieves a $1/e$-regret bound of $O(T^{4/5})$. Next, we extend Mono-MFW to the bandit setting and propose the Bandit-MFW algorithm which attains a $1/e$-regret bound of $O(T^{8/9})$. To the best of our knowledge, Mono-MFW and Bandit-MFW are the first sublinear-regret algorithms to explore the one-shot and bandit setting for online non-monotone continuous DR-submodular maximization problem over a down-closed convex set, respectively. Finally, we conduct numerical experiments on both synthetic and real-world datasets to verify the effectiveness of our methods.

MNL-Bandits under Inventory and Limited Switches Constraints

Optimizing the assortment of products to display to customers is a key to increasing revenue for both offline and online retailers. To trade-off between exploring customers' preference and exploiting customers' choices learned from data, in this paper, by adopting the Multi-Nomial Logit (MNL) choice model to capture customers' choices over products, we study the problem of optimizing assortments over a planning horizon $T$ for maximizing the profit of the retailer. To make the problem setting more practical, we consider both the inventory constraint and the limited switches constraint, where the retailer cannot use up the resource inventory before time $T$ and is forbidden to switch the assortment shown to customers too many times. Such a setting suits the case when an online retailer wants to dynamically optimize the assortment selection for a population of customers. We develop an efficient UCB-like algorithm to optimize the assortments while learning customers' choices from data. We prove that our algorithm can achieve a sub-linear regret bound $\tilde{O}\left(T^{1-\alpha/2}\right)$ if $O(T^\alpha)$ switches are allowed. %, and our regret bound is optimal with respect to $T$. Extensive numerical experiments show that our algorithm outperforms baselines and the gap between our algorithm's performance and the theoretical upper bound is small.

Continuous Submodular Maximization: Boosting via Non-oblivious Function

In this paper, we revisit the constrained and stochastic continuous submodular maximization in both offline and online settings. For each $\gamma$-weakly DR-submodular function $f$, we use the factor-revealing optimization equation to derive an optimal auxiliary function $F$, whose stationary points provide a $(1-e^{-\gamma})$-approximation to the global maximum value (denoted as $OPT$) of problem $\max_{\boldsymbol{x}\in\mathcal{C}}f(\boldsymbol{x})$. Naturally, the projected (mirror) gradient ascent relied on this non-oblivious function achieves $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{2})$ iterations, beating the traditional $(\frac{\gamma^{2}}{1+\gamma^{2}})$-approximation gradient ascent \citep{hassani2017gradient} for submodular maximization. Similarly, based on $F$, the classical Frank-Wolfe algorithm equipped with variance reduction technique \citep{mokhtari2018conditional} also returns a solution with objective value larger than $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{3})$ iterations. In the online setting, we first consider the adversarial delays for stochastic gradient feedback, under which we propose a boosting online gradient algorithm with the same non-oblivious search, achieving a regret of $\sqrt{D}$ (where $D$ is the sum of delays of gradient feedback) against a $(1-e^{-\gamma})$-approximation to the best feasible solution in hindsight. Finally, extensive numerical experiments demonstrate the efficiency of our boosting methods.

Online Allocation with Two-sided Resource Constraints

Motivated by many interesting real-world applications in logistics and online advertising, we consider an online allocation problem subject to lower and upper resource constraints, where the requests arrive sequentially, sampled i.i.d. from an unknown distribution, and we need to promptly make a decision given limited resources and lower bounds requirements. First, with knowledge of the measure of feasibility, i.e., $\alpha$, we propose a new algorithm that obtains $1-O(\frac{\epsilon}{\alpha-\epsilon})$ -competitive ratio for the offline problems that know the entire requests ahead of time. Inspired by the previous studies, this algorithm adopts an innovative technique to dynamically update a threshold price vector for making decisions. Moreover, an optimization method to estimate the optimal measure of feasibility is proposed with theoretical guarantee at the end of this paper. Based on this method, if we tolerate slight violation of the lower bounds constraints with parameter $\eta$, the proposed algorithm is naturally extended to the settings without strong feasible assumption, which cover the significantly unexplored infeasible scenarios.