In-Context Former: Lightning-fast Compressing Context for Large Language Model

With the rising popularity of Transformer-based large language models (LLMs), reducing their high inference costs has become a significant research focus. One effective approach is to compress the long input contexts. Existing methods typically leverage the self-attention mechanism of the LLM itself for context compression. While these methods have achieved notable results, the compression process still involves quadratic time complexity, which limits their applicability. To mitigate this limitation, we propose the In-Context Former (IC-Former). Unlike previous methods, IC-Former does not depend on the target LLMs. Instead, it leverages the cross-attention mechanism and a small number of learnable digest tokens to directly condense information from the contextual word embeddings. This approach significantly reduces inference time, which achieves linear growth in time complexity within the compression range. Experimental results indicate that our method requires only 1/32 of the floating-point operations of the baseline during compression and improves processing speed by 68 to 112 times while achieving over 90% of the baseline performance on evaluation metrics. Overall, our model effectively reduces compression costs and makes real-time compression scenarios feasible.

Boosting Gradient Ascent for Continuous DR-submodular Maximization

Projected Gradient Ascent (PGA) is the most commonly used optimization scheme in machine learning and operations research areas. Nevertheless, numerous studies and examples have shown that the PGA methods may fail to achieve the tight approximation ratio for continuous DR-submodular maximization problems. To address this challenge, we present a boosting technique in this paper, which can efficiently improve the approximation guarantee of the standard PGA to \emph{optimal} with only small modifications on the objective function. The fundamental idea of our boosting technique is to exploit non-oblivious search to derive a novel auxiliary function $F$, whose stationary points are excellent approximations to the global maximum of the original DR-submodular objective $f$. Specifically, when $f$ is monotone and $\gamma$-weakly DR-submodular, we propose an auxiliary function $F$ whose stationary points can provide a better $(1-e^{-\gamma})$-approximation than the $(\gamma^2/(1+\gamma^2))$-approximation guaranteed by the stationary points of $f$ itself. Similarly, for the non-monotone case, we devise another auxiliary function $F$ whose stationary points can achieve an optimal $\frac{1-\min_{\boldsymbol{x}\in\mathcal{C}}\|\boldsymbol{x}\|_{\infty}}{4}$-approximation guarantee where $\mathcal{C}$ is a convex constraint set. In contrast, the stationary points of the original non-monotone DR-submodular function can be arbitrarily bad~\citep{chen2023continuous}. Furthermore, we demonstrate the scalability of our boosting technique on four problems. In all of these four problems, our resulting variants of boosting PGA algorithm beat the previous standard PGA in several aspects such as approximation ratio and efficiency. Finally, we corroborate our theoretical findings with numerical experiments, which demonstrate the effectiveness of our boosting PGA methods.

An Online Algorithm for Chance Constrained Resource Allocation

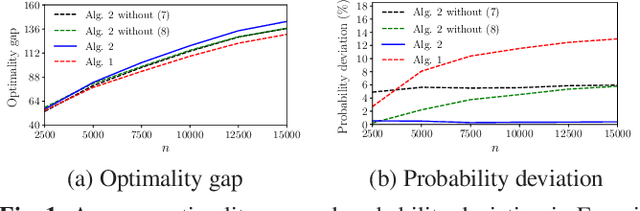
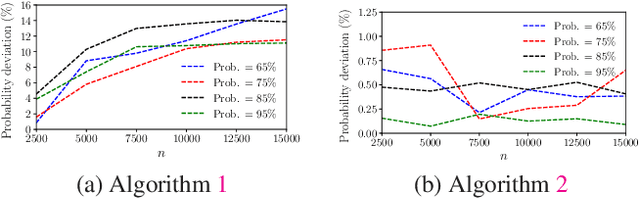
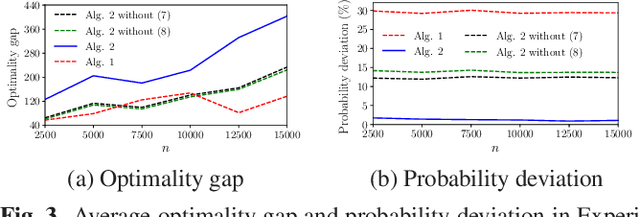
This paper studies the online stochastic resource allocation problem (RAP) with chance constraints. The online RAP is a 0-1 integer linear programming problem where the resource consumption coefficients are revealed column by column along with the corresponding revenue coefficients. When a column is revealed, the corresponding decision variables are determined instantaneously without future information. Moreover, in online applications, the resource consumption coefficients are often obtained by prediction. To model their uncertainties, we take the chance constraints into the consideration. To the best of our knowledge, this is the first time chance constraints are introduced in the online RAP problem. Assuming that the uncertain variables have known Gaussian distributions, the stochastic RAP can be transformed into a deterministic but nonlinear problem with integer second-order cone constraints. Next, we linearize this nonlinear problem and analyze the performance of vanilla online primal-dual algorithm for solving the linearized stochastic RAP. Under mild technical assumptions, the optimality gap and constraint violation are both on the order of $\sqrt{n}$. Then, to further improve the performance of the algorithm, several modified online primal-dual algorithms with heuristic corrections are proposed. Finally, extensive numerical experiments on both synthetic and real data demonstrate the applicability and effectiveness of our methods.

Communication-Efficient Decentralized Online Continuous DR-Submodular Maximization

Maximizing a monotone submodular function is a fundamental task in machine learning, economics, and statistics. In this paper, we present two communication-efficient decentralized online algorithms for the monotone continuous DR-submodular maximization problem, both of which reduce the number of per-function gradient evaluations and per-round communication complexity from $T^{3/2}$ to $1$. The first one, One-shot Decentralized Meta-Frank-Wolfe (Mono-DMFW), achieves a $(1-1/e)$-regret bound of $O(T^{4/5})$. As far as we know, this is the first one-shot and projection-free decentralized online algorithm for monotone continuous DR-submodular maximization. Next, inspired by the non-oblivious boosting function \citep{zhang2022boosting}, we propose the Decentralized Online Boosting Gradient Ascent (DOBGA) algorithm, which attains a $(1-1/e)$-regret of $O(\sqrt{T})$. To the best of our knowledge, this is the first result to obtain the optimal $O(\sqrt{T})$ against a $(1-1/e)$-approximation with only one gradient inquiry for each local objective function per step. Finally, various experimental results confirm the effectiveness of the proposed methods.

Online Learning for Non-monotone Submodular Maximization: From Full Information to Bandit Feedback

In this paper, we revisit the online non-monotone continuous DR-submodular maximization problem over a down-closed convex set, which finds wide real-world applications in the domain of machine learning, economics, and operations research. At first, we present the Meta-MFW algorithm achieving a $1/e$-regret of $O(\sqrt{T})$ at the cost of $T^{3/2}$ stochastic gradient evaluations per round. As far as we know, Meta-MFW is the first algorithm to obtain $1/e$-regret of $O(\sqrt{T})$ for the online non-monotone continuous DR-submodular maximization problem over a down-closed convex set. Furthermore, in sharp contrast with ODC algorithm \citep{thang2021online}, Meta-MFW relies on the simple online linear oracle without discretization, lifting, or rounding operations. Considering the practical restrictions, we then propose the Mono-MFW algorithm, which reduces the per-function stochastic gradient evaluations from $T^{3/2}$ to 1 and achieves a $1/e$-regret bound of $O(T^{4/5})$. Next, we extend Mono-MFW to the bandit setting and propose the Bandit-MFW algorithm which attains a $1/e$-regret bound of $O(T^{8/9})$. To the best of our knowledge, Mono-MFW and Bandit-MFW are the first sublinear-regret algorithms to explore the one-shot and bandit setting for online non-monotone continuous DR-submodular maximization problem over a down-closed convex set, respectively. Finally, we conduct numerical experiments on both synthetic and real-world datasets to verify the effectiveness of our methods.

Continuous Submodular Maximization: Boosting via Non-oblivious Function

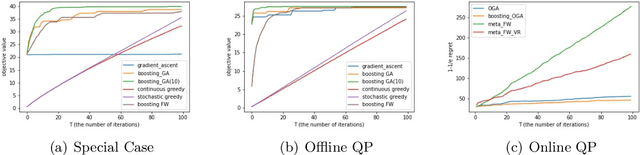
In this paper, we revisit the constrained and stochastic continuous submodular maximization in both offline and online settings. For each $\gamma$-weakly DR-submodular function $f$, we use the factor-revealing optimization equation to derive an optimal auxiliary function $F$, whose stationary points provide a $(1-e^{-\gamma})$-approximation to the global maximum value (denoted as $OPT$) of problem $\max_{\boldsymbol{x}\in\mathcal{C}}f(\boldsymbol{x})$. Naturally, the projected (mirror) gradient ascent relied on this non-oblivious function achieves $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{2})$ iterations, beating the traditional $(\frac{\gamma^{2}}{1+\gamma^{2}})$-approximation gradient ascent \citep{hassani2017gradient} for submodular maximization. Similarly, based on $F$, the classical Frank-Wolfe algorithm equipped with variance reduction technique \citep{mokhtari2018conditional} also returns a solution with objective value larger than $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{3})$ iterations. In the online setting, we first consider the adversarial delays for stochastic gradient feedback, under which we propose a boosting online gradient algorithm with the same non-oblivious search, achieving a regret of $\sqrt{D}$ (where $D$ is the sum of delays of gradient feedback) against a $(1-e^{-\gamma})$-approximation to the best feasible solution in hindsight. Finally, extensive numerical experiments demonstrate the efficiency of our boosting methods.

Online Allocation with Two-sided Resource Constraints

Motivated by many interesting real-world applications in logistics and online advertising, we consider an online allocation problem subject to lower and upper resource constraints, where the requests arrive sequentially, sampled i.i.d. from an unknown distribution, and we need to promptly make a decision given limited resources and lower bounds requirements. First, with knowledge of the measure of feasibility, i.e., $\alpha$, we propose a new algorithm that obtains $1-O(\frac{\epsilon}{\alpha-\epsilon})$ -competitive ratio for the offline problems that know the entire requests ahead of time. Inspired by the previous studies, this algorithm adopts an innovative technique to dynamically update a threshold price vector for making decisions. Moreover, an optimization method to estimate the optimal measure of feasibility is proposed with theoretical guarantee at the end of this paper. Based on this method, if we tolerate slight violation of the lower bounds constraints with parameter $\eta$, the proposed algorithm is naturally extended to the settings without strong feasible assumption, which cover the significantly unexplored infeasible scenarios.

Adam revisited: a weighted past gradients perspective

Adaptive learning rate methods have been successfully applied in many fields, especially in training deep neural networks. Recent results have shown that adaptive methods with exponential increasing weights on squared past gradients (i.e., ADAM, RMSPROP) may fail to converge to the optimal solution. Though many algorithms, such as AMSGRAD and ADAMNC, have been proposed to fix the non-convergence issues, achieving a data-dependent regret bound similar to or better than ADAGRAD is still a challenge to these methods. In this paper, we propose a novel adaptive method weighted adaptive algorithm (WADA) to tackle the non-convergence issues. Unlike AMSGRAD and ADAMNC, we consider using a milder growing weighting strategy on squared past gradient, in which weights grow linearly. Based on this idea, we propose weighted adaptive gradient method framework (WAGMF) and implement WADA algorithm on this framework. Moreover, we prove that WADA can achieve a weighted data-dependent regret bound, which could be better than the original regret bound of ADAGRAD when the gradients decrease rapidly. This bound may partially explain the good performance of ADAM in practice. Finally, extensive experiments demonstrate the effectiveness of WADA and its variants in comparison with several variants of ADAM on training convex problems and deep neural networks.

Symmetric Cross Entropy for Robust Learning with Noisy Labels

Training accurate deep neural networks (DNNs) in the presence of noisy labels is an important and challenging task. Though a number of approaches have been proposed for learning with noisy labels, many open issues remain. In this paper, we show that DNN learning with Cross Entropy (CE) exhibits overfitting to noisy labels on some classes ("easy" classes), but more surprisingly, it also suffers from significant under learning on some other classes ("hard" classes). Intuitively, CE requires an extra term to facilitate learning of hard classes, and more importantly, this term should be noise tolerant, so as to avoid overfitting to noisy labels. Inspired by the symmetric KL-divergence, we propose the approach of \textbf{Symmetric cross entropy Learning} (SL), boosting CE symmetrically with a noise robust counterpart Reverse Cross Entropy (RCE). Our proposed SL approach simultaneously addresses both the under learning and overfitting problem of CE in the presence of noisy labels. We provide a theoretical analysis of SL and also empirically show, on a range of benchmark and real-world datasets, that SL outperforms state-of-the-art methods. We also show that SL can be easily incorporated into existing methods in order to further enhance their performance.

Joint Semantic Domain Alignment and Target Classifier Learning for Unsupervised Domain Adaptation

Unsupervised domain adaptation aims to transfer the classifier learned from the source domain to the target domain in an unsupervised manner. With the help of target pseudo-labels, aligning class-level distributions and learning the classifier in the target domain are two widely used objectives. Existing methods often separately optimize these two individual objectives, which makes them suffer from the neglect of the other. However, optimizing these two aspects together is not trivial. To alleviate the above issues, we propose a novel method that jointly optimizes semantic domain alignment and target classifier learning in a holistic way. The joint optimization mechanism can not only eliminate their weaknesses but also complement their strengths. The theoretical analysis also verifies the favor of the joint optimization mechanism. Extensive experiments on benchmark datasets show that the proposed method yields the best performance in comparison with the state-of-the-art unsupervised domain adaptation methods.