Continuous Submodular Maximization: Boosting via Non-oblivious Function
Paper and Code
Jan 03, 2022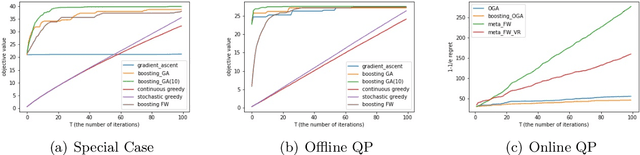
In this paper, we revisit the constrained and stochastic continuous submodular maximization in both offline and online settings. For each $\gamma$-weakly DR-submodular function $f$, we use the factor-revealing optimization equation to derive an optimal auxiliary function $F$, whose stationary points provide a $(1-e^{-\gamma})$-approximation to the global maximum value (denoted as $OPT$) of problem $\max_{\boldsymbol{x}\in\mathcal{C}}f(\boldsymbol{x})$. Naturally, the projected (mirror) gradient ascent relied on this non-oblivious function achieves $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{2})$ iterations, beating the traditional $(\frac{\gamma^{2}}{1+\gamma^{2}})$-approximation gradient ascent \citep{hassani2017gradient} for submodular maximization. Similarly, based on $F$, the classical Frank-Wolfe algorithm equipped with variance reduction technique \citep{mokhtari2018conditional} also returns a solution with objective value larger than $(1-e^{-\gamma}-\epsilon^{2})OPT-\epsilon$ after $O(1/\epsilon^{3})$ iterations. In the online setting, we first consider the adversarial delays for stochastic gradient feedback, under which we propose a boosting online gradient algorithm with the same non-oblivious search, achieving a regret of $\sqrt{D}$ (where $D$ is the sum of delays of gradient feedback) against a $(1-e^{-\gamma})$-approximation to the best feasible solution in hindsight. Finally, extensive numerical experiments demonstrate the efficiency of our boosting methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge