Module-wise Adaptive Adversarial Training for End-to-end Autonomous Driving

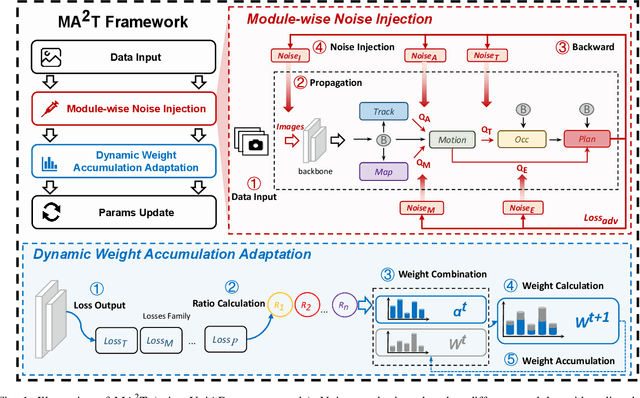
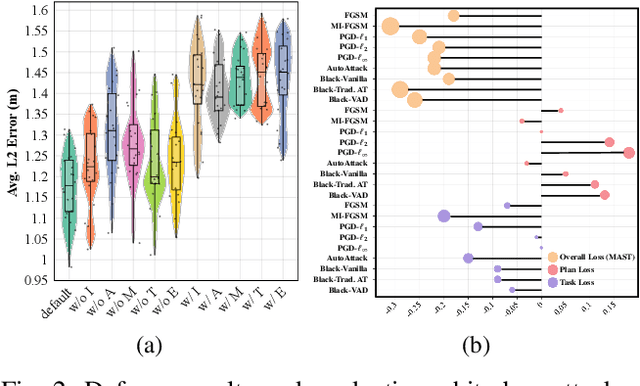
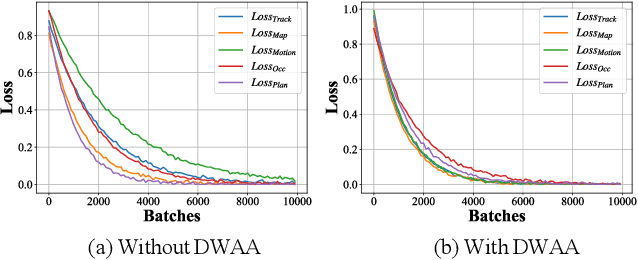
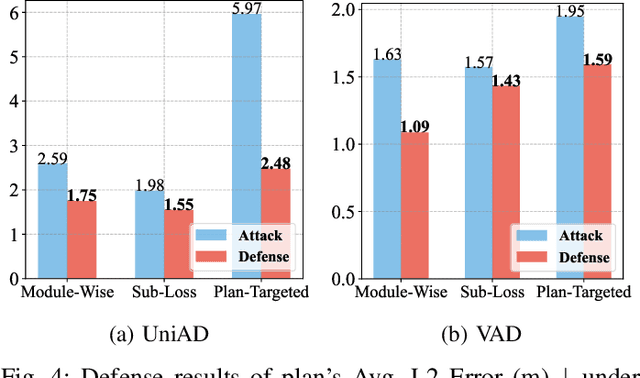
Recent advances in deep learning have markedly improved autonomous driving (AD) models, particularly end-to-end systems that integrate perception, prediction, and planning stages, achieving state-of-the-art performance. However, these models remain vulnerable to adversarial attacks, where human-imperceptible perturbations can disrupt decision-making processes. While adversarial training is an effective method for enhancing model robustness against such attacks, no prior studies have focused on its application to end-to-end AD models. In this paper, we take the first step in adversarial training for end-to-end AD models and present a novel Module-wise Adaptive Adversarial Training (MA2T). However, extending conventional adversarial training to this context is highly non-trivial, as different stages within the model have distinct objectives and are strongly interconnected. To address these challenges, MA2T first introduces Module-wise Noise Injection, which injects noise before the input of different modules, targeting training models with the guidance of overall objectives rather than each independent module loss. Additionally, we introduce Dynamic Weight Accumulation Adaptation, which incorporates accumulated weight changes to adaptively learn and adjust the loss weights of each module based on their contributions (accumulated reduction rates) for better balance and robust training. To demonstrate the efficacy of our defense, we conduct extensive experiments on the widely-used nuScenes dataset across several end-to-end AD models under both white-box and black-box attacks, where our method outperforms other baselines by large margins (+5-10%). Moreover, we validate the robustness of our defense through closed-loop evaluation in the CARLA simulation environment, showing improved resilience even against natural corruption.

Comparing remote sensing-based forest biomass mapping approaches using new forest inventory plots in contrasting forests in northeastern and southwestern China

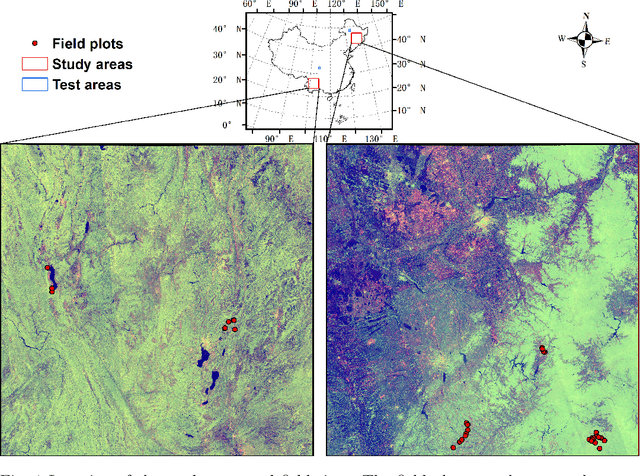
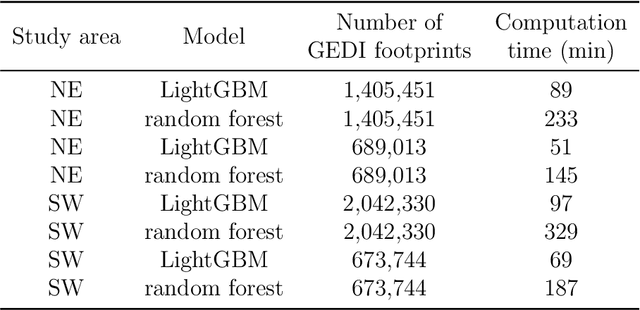
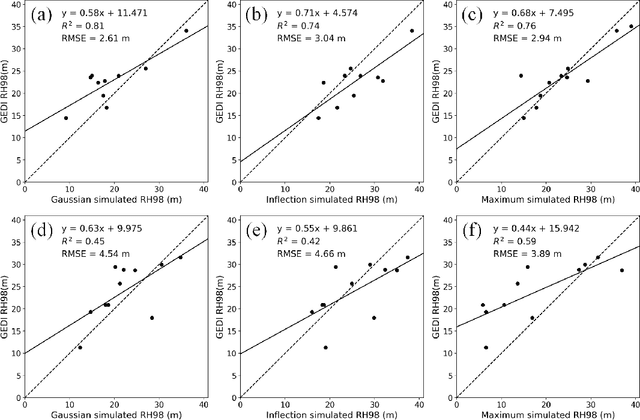
Large-scale high spatial resolution aboveground biomass (AGB) maps play a crucial role in determining forest carbon stocks and how they are changing, which is instrumental in understanding the global carbon cycle, and implementing policy to mitigate climate change. The advent of the new space-borne LiDAR sensor, NASA's GEDI instrument, provides unparalleled possibilities for the accurate and unbiased estimation of forest AGB at high resolution, particularly in dense and tall forests, where Synthetic Aperture Radar (SAR) and passive optical data exhibit saturation. However, GEDI is a sampling instrument, collecting dispersed footprints, and its data must be combined with that from other continuous cover satellites to create high-resolution maps, using local machine learning methods. In this study, we developed local models to estimate forest AGB from GEDI L2A data, as the models used to create GEDI L4 AGB data incorporated minimal field data from China. We then applied LightGBM and random forest regression to generate wall-to-wall AGB maps at 25 m resolution, using extensive GEDI footprints as well as Sentinel-1 data, ALOS-2 PALSAR-2 and Sentinel-2 optical data. Through a 5-fold cross-validation, LightGBM demonstrated a slightly better performance than Random Forest across two contrasting regions. However, in both regions, the computation speed of LightGBM is substantially faster than that of the random forest model, requiring roughly one-third of the time to compute on the same hardware. Through the validation against field data, the 25 m resolution AGB maps generated using the local models developed in this study exhibited higher accuracy compared to the GEDI L4B AGB data. We found in both regions an increase in error as slope increased. The trained models were tested on nearby but different regions and exhibited good performance.

An Online Algorithm for Chance Constrained Resource Allocation

This paper studies the online stochastic resource allocation problem (RAP) with chance constraints. The online RAP is a 0-1 integer linear programming problem where the resource consumption coefficients are revealed column by column along with the corresponding revenue coefficients. When a column is revealed, the corresponding decision variables are determined instantaneously without future information. Moreover, in online applications, the resource consumption coefficients are often obtained by prediction. To model their uncertainties, we take the chance constraints into the consideration. To the best of our knowledge, this is the first time chance constraints are introduced in the online RAP problem. Assuming that the uncertain variables have known Gaussian distributions, the stochastic RAP can be transformed into a deterministic but nonlinear problem with integer second-order cone constraints. Next, we linearize this nonlinear problem and analyze the performance of vanilla online primal-dual algorithm for solving the linearized stochastic RAP. Under mild technical assumptions, the optimality gap and constraint violation are both on the order of $\sqrt{n}$. Then, to further improve the performance of the algorithm, several modified online primal-dual algorithms with heuristic corrections are proposed. Finally, extensive numerical experiments on both synthetic and real data demonstrate the applicability and effectiveness of our methods.

Range Resolution Enhanced Method with Spectral Properties for Hyperspectral Lidar

Waveform decomposition is needed as a first step in the extraction of various types of geometric and spectral information from hyperspectral full-waveform LiDAR echoes. We present a new approach to deal with the "Pseudo-monopulse" waveform formed by the overlapped waveforms from multi-targets when they are very close. We use one single skew-normal distribution (SND) model to fit waveforms of all spectral channels first and count the geometric center position distribution of the echoes to decide whether it contains multi-targets. The geometric center position distribution of the "Pseudo-monopulse" presents aggregation and asymmetry with the change of wavelength, while such an asymmetric phenomenon cannot be found from the echoes of the single target. Both theoretical and experimental data verify the point. Based on such observation, we further propose a hyperspectral waveform decomposition method utilizing the SND mixture model with: 1) initializing new waveform component parameters and their ranges based on the distinction of the three characteristics (geometric center position, pulse width, and skew-coefficient) between the echo and fitted SND waveform and 2) conducting single-channel waveform decomposition for all channels and 3) setting thresholds to find outlier channels based on statistical parameters of all single-channel decomposition results (the standard deviation and the means of geometric center position) and 4) re-conducting single-channel waveform decomposition for these outlier channels. The proposed method significantly improves the range resolution from 60cm to 5cm at most for a 4ns width laser pulse and represents the state-of-the-art in "Pseudo-monopulse" waveform decomposition.

T-SNE Is Not Optimized to Reveal Clusters in Data

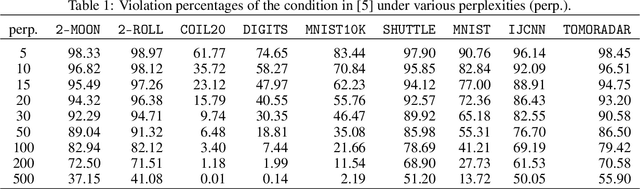
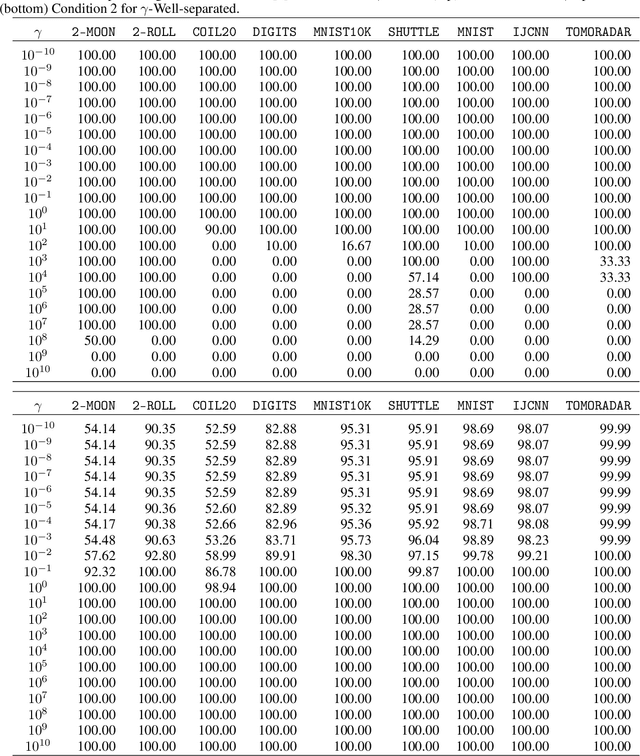
Cluster visualization is an essential task for nonlinear dimensionality reduction as a data analysis tool. It is often believed that Student t-Distributed Stochastic Neighbor Embedding (t-SNE) can show clusters for well clusterable data, with a smaller Kullback-Leibler divergence corresponding to a better quality. There was even theoretical proof for the guarantee of this property. However, we point out that this is not necessarily the case -- t-SNE may leave clustering patterns hidden despite strong signals present in the data. Extensive empirical evidence is provided to support our claim. First, several real-world counter-examples are presented, where t-SNE fails even if the input neighborhoods are well clusterable. Tuning hyperparameters in t-SNE or using better optimization algorithms does not help solve this issue because a better t-SNE learning objective can correspond to a worse cluster embedding. Second, we check the assumptions in the clustering guarantee of t-SNE and find they are often violated for real-world data sets.

Stochastic Cluster Embedding

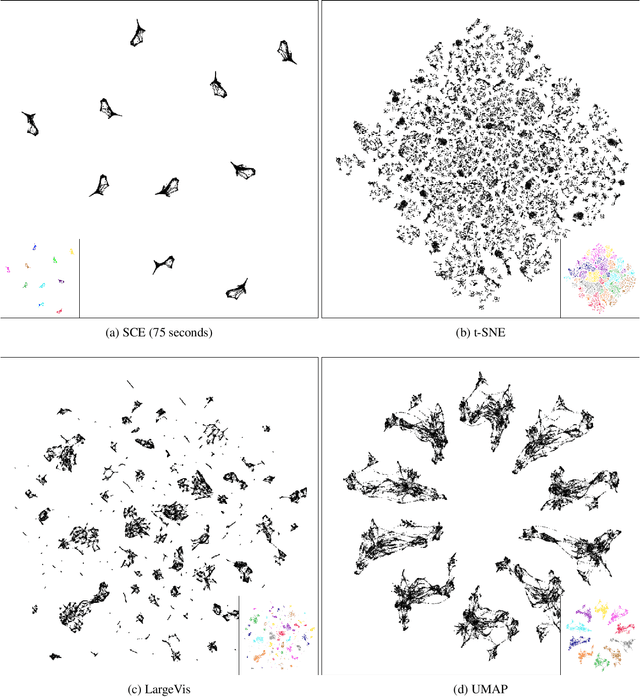
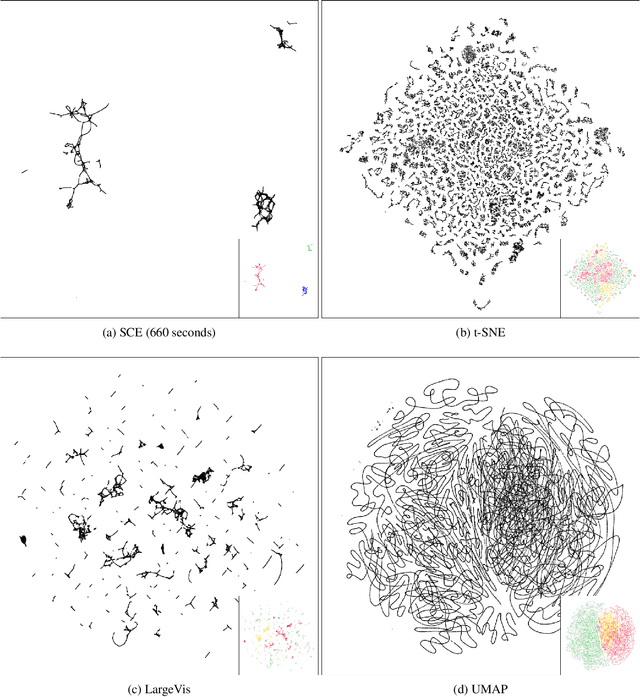
Neighbor Embedding (NE) that aims to preserve pairwise similarities between data items has been shown to yield an effective principle for data visualization. However, even the currently best NE methods such as Stochastic Neighbor Embedding (SNE) may leave large-scale patterns such as clusters hidden despite of strong signals being present in the data. To address this, we propose a new cluster visualization method based on Neighbor Embedding. We first present a family of Neighbor Embedding methods which generalizes SNE by using non-normalized Kullback-Leibler divergence with a scale parameter. In this family, much better cluster visualizations often appear with a parameter value different from the one corresponding to SNE. We also develop an efficient software which employs asynchronous stochastic block coordinate descent to optimize the new family of objective functions. The experimental results demonstrate that our method consistently and substantially improves visualization of data clusters compared with the state-of-the-art NE approaches.