Near-Optimal Online Learning for Multi-Agent Submodular Coordination: Tight Approximation and Communication Efficiency

Coordinating multiple agents to collaboratively maximize submodular functions in unpredictable environments is a critical task with numerous applications in machine learning, robot planning and control. The existing approaches, such as the OSG algorithm, are often hindered by their poor approximation guarantees and the rigid requirement for a fully connected communication graph. To address these challenges, we firstly present a $\textbf{MA-OSMA}$ algorithm, which employs the multi-linear extension to transfer the discrete submodular maximization problem into a continuous optimization, thereby allowing us to reduce the strict dependence on a complete graph through consensus techniques. Moreover, $\textbf{MA-OSMA}$ leverages a novel surrogate gradient to avoid sub-optimal stationary points. To eliminate the computationally intensive projection operations in $\textbf{MA-OSMA}$, we also introduce a projection-free $\textbf{MA-OSEA}$ algorithm, which effectively utilizes the KL divergence by mixing a uniform distribution. Theoretically, we confirm that both algorithms achieve a regret bound of $\widetilde{O}(\sqrt{\frac{C_{T}T}{1-\beta}})$ against a $(\frac{1-e^{-c}}{c})$-approximation to the best comparator in hindsight, where $C_{T}$ is the deviation of maximizer sequence, $\beta$ is the spectral gap of the network and $c$ is the joint curvature of submodular objectives. This result significantly improves the $(\frac{1}{1+c})$-approximation provided by the state-of-the-art OSG algorithm. Finally, we demonstrate the effectiveness of our proposed algorithms through simulation-based multi-target tracking.

Boosting Gradient Ascent for Continuous DR-submodular Maximization

Projected Gradient Ascent (PGA) is the most commonly used optimization scheme in machine learning and operations research areas. Nevertheless, numerous studies and examples have shown that the PGA methods may fail to achieve the tight approximation ratio for continuous DR-submodular maximization problems. To address this challenge, we present a boosting technique in this paper, which can efficiently improve the approximation guarantee of the standard PGA to \emph{optimal} with only small modifications on the objective function. The fundamental idea of our boosting technique is to exploit non-oblivious search to derive a novel auxiliary function $F$, whose stationary points are excellent approximations to the global maximum of the original DR-submodular objective $f$. Specifically, when $f$ is monotone and $\gamma$-weakly DR-submodular, we propose an auxiliary function $F$ whose stationary points can provide a better $(1-e^{-\gamma})$-approximation than the $(\gamma^2/(1+\gamma^2))$-approximation guaranteed by the stationary points of $f$ itself. Similarly, for the non-monotone case, we devise another auxiliary function $F$ whose stationary points can achieve an optimal $\frac{1-\min_{\boldsymbol{x}\in\mathcal{C}}\|\boldsymbol{x}\|_{\infty}}{4}$-approximation guarantee where $\mathcal{C}$ is a convex constraint set. In contrast, the stationary points of the original non-monotone DR-submodular function can be arbitrarily bad~\citep{chen2023continuous}. Furthermore, we demonstrate the scalability of our boosting technique on four problems. In all of these four problems, our resulting variants of boosting PGA algorithm beat the previous standard PGA in several aspects such as approximation ratio and efficiency. Finally, we corroborate our theoretical findings with numerical experiments, which demonstrate the effectiveness of our boosting PGA methods.

Bandit Multi-linear DR-Submodular Maximization and Its Applications on Adversarial Submodular Bandits

We investigate the online bandit learning of the monotone multi-linear DR-submodular functions, designing the algorithm $\mathtt{BanditMLSM}$ that attains $O(T^{2/3}\log T)$ of $(1-1/e)$-regret. Then we reduce submodular bandit with partition matroid constraint and bandit sequential monotone maximization to the online bandit learning of the monotone multi-linear DR-submodular functions, attaining $O(T^{2/3}\log T)$ of $(1-1/e)$-regret in both problems, which improve the existing results. To the best of our knowledge, we are the first to give a sublinear regret algorithm for the submodular bandit with partition matroid constraint. A special case of this problem is studied by Streeter et al.(2009). They prove a $O(T^{4/5})$ $(1-1/e)$-regret upper bound. For the bandit sequential submodular maximization, the existing work proves an $O(T^{2/3})$ regret with a suboptimal $1/2$ approximation ratio (Niazadeh et al. 2021).

Quantum Multi-Armed Bandits and Stochastic Linear Bandits Enjoy Logarithmic Regrets

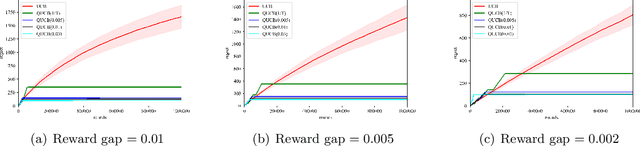
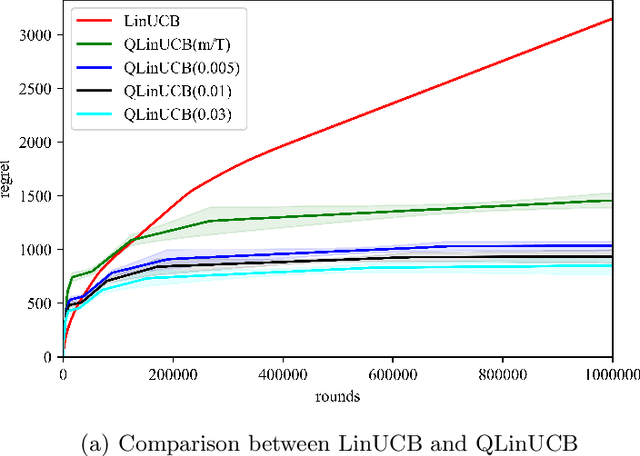
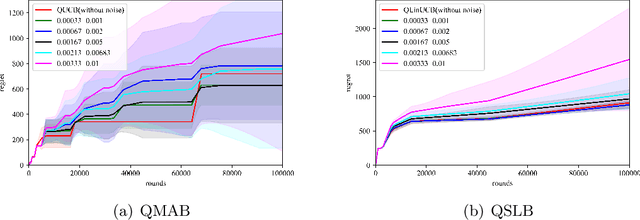
Multi-arm bandit (MAB) and stochastic linear bandit (SLB) are important models in reinforcement learning, and it is well-known that classical algorithms for bandits with time horizon $T$ suffer $\Omega(\sqrt{T})$ regret. In this paper, we study MAB and SLB with quantum reward oracles and propose quantum algorithms for both models with $O(\mbox{poly}(\log T))$ regrets, exponentially improving the dependence in terms of $T$. To the best of our knowledge, this is the first provable quantum speedup for regrets of bandit problems and in general exploitation in reinforcement learning. Compared to previous literature on quantum exploration algorithms for MAB and reinforcement learning, our quantum input model is simpler and only assumes quantum oracles for each individual arm.

Bounded Memory Adversarial Bandits with Composite Anonymous Delayed Feedback

We study the adversarial bandit problem with composite anonymous delayed feedback. In this setting, losses of an action are split into $d$ components, spreading over consecutive rounds after the action is chosen. And in each round, the algorithm observes the aggregation of losses that come from the latest $d$ rounds. Previous works focus on oblivious adversarial setting, while we investigate the harder non-oblivious setting. We show non-oblivious setting incurs $\Omega(T)$ pseudo regret even when the loss sequence is bounded memory. However, we propose a wrapper algorithm which enjoys $o(T)$ policy regret on many adversarial bandit problems with the assumption that the loss sequence is bounded memory. Especially, for $K$-armed bandit and bandit convex optimization, we have $\mathcal{O}(T^{2/3})$ policy regret bound. We also prove a matching lower bound for $K$-armed bandit. Our lower bound works even when the loss sequence is oblivious but the delay is non-oblivious. It answers the open problem proposed in \cite{wang2021adaptive}, showing that non-oblivious delay is enough to incur $\tilde{\Omega}(T^{2/3})$ regret.