Quantum Multi-Armed Bandits and Stochastic Linear Bandits Enjoy Logarithmic Regrets
Paper and Code
May 30, 2022
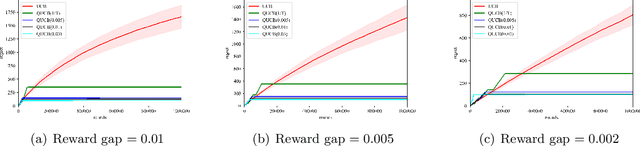
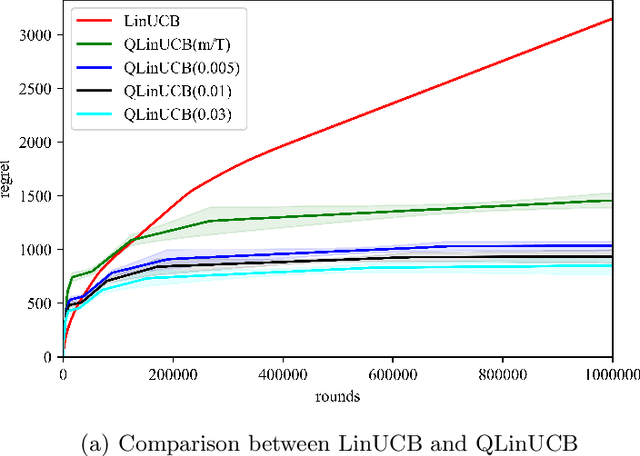
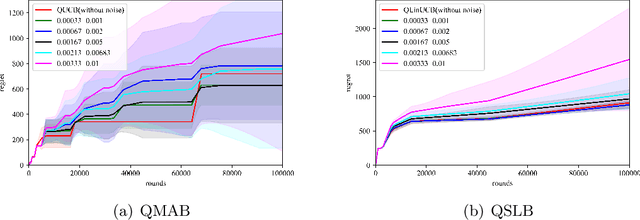
Multi-arm bandit (MAB) and stochastic linear bandit (SLB) are important models in reinforcement learning, and it is well-known that classical algorithms for bandits with time horizon $T$ suffer $\Omega(\sqrt{T})$ regret. In this paper, we study MAB and SLB with quantum reward oracles and propose quantum algorithms for both models with $O(\mbox{poly}(\log T))$ regrets, exponentially improving the dependence in terms of $T$. To the best of our knowledge, this is the first provable quantum speedup for regrets of bandit problems and in general exploitation in reinforcement learning. Compared to previous literature on quantum exploration algorithms for MAB and reinforcement learning, our quantum input model is simpler and only assumes quantum oracles for each individual arm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge