Local Linear Convergence of Infeasible Optimization with Orthogonal Constraints

Many classical and modern machine learning algorithms require solving optimization tasks under orthogonality constraints. Solving these tasks with feasible methods requires a gradient descent update followed by a retraction operation on the Stiefel manifold, which can be computationally expensive. Recently, an infeasible retraction-free approach, termed the landing algorithm, was proposed as an efficient alternative. Motivated by the common occurrence of orthogonality constraints in tasks such as principle component analysis and training of deep neural networks, this paper studies the landing algorithm and establishes a novel linear convergence rate for smooth non-convex functions using only a local Riemannian P{\L} condition. Numerical experiments demonstrate that the landing algorithm performs on par with the state-of-the-art retraction-based methods with substantially reduced computational overhead.

Global Convergence of Decentralized Retraction-Free Optimization on the Stiefel Manifold

Many classical and modern machine learning algorithms require solving optimization tasks under orthogonal constraints. Solving these tasks often require calculating retraction-based gradient descent updates on the corresponding Riemannian manifold, which can be computationally expensive. Recently Ablin et al. proposed an infeasible retraction-free algorithm, which is significantly more efficient. In this paper, we study the decentralized non-convex optimization task over a network of agents on the Stiefel manifold with retraction-free updates. We propose \textbf{D}ecentralized \textbf{R}etraction-\textbf{F}ree \textbf{G}radient \textbf{T}racking (DRFGT) algorithm, and show that DRFGT exhibits ergodic $\mathcal{O}(1/K)$ convergence rate, the same rate of convergence as the centralized, retraction-based methods. We also provide numerical experiments demonstrating that DRFGT performs on par with the state-of-the-art retraction based methods with substantially reduced computational overhead.

FedLALR: Client-Specific Adaptive Learning Rates Achieve Linear Speedup for Non-IID Data

Federated learning is an emerging distributed machine learning method, enables a large number of clients to train a model without exchanging their local data. The time cost of communication is an essential bottleneck in federated learning, especially for training large-scale deep neural networks. Some communication-efficient federated learning methods, such as FedAvg and FedAdam, share the same learning rate across different clients. But they are not efficient when data is heterogeneous. To maximize the performance of optimization methods, the main challenge is how to adjust the learning rate without hurting the convergence. In this paper, we propose a heterogeneous local variant of AMSGrad, named FedLALR, in which each client adjusts its learning rate based on local historical gradient squares and synchronized learning rates. Theoretical analysis shows that our client-specified auto-tuned learning rate scheduling can converge and achieve linear speedup with respect to the number of clients, which enables promising scalability in federated optimization. We also empirically compare our method with several communication-efficient federated optimization methods. Extensive experimental results on Computer Vision (CV) tasks and Natural Language Processing (NLP) task show the efficacy of our proposed FedLALR method and also coincides with our theoretical findings.

Dynamic Regularized Sharpness Aware Minimization in Federated Learning: Approaching Global Consistency and Smooth Landscape

In federated learning (FL), a cluster of local clients are chaired under the coordination of the global server and cooperatively train one model with privacy protection. Due to the multiple local updates and the isolated non-iid dataset, clients are prone to overfit into their own optima, which extremely deviates from the global objective and significantly undermines the performance. Most previous works only focus on enhancing the consistency between the local and global objectives to alleviate this prejudicial client drifts from the perspective of the optimization view, whose performance would be prominently deteriorated on the high heterogeneity. In this work, we propose a novel and general algorithm {\ttfamily FedSMOO} by jointly considering the optimization and generalization targets to efficiently improve the performance in FL. Concretely, {\ttfamily FedSMOO} adopts a dynamic regularizer to guarantee the local optima towards the global objective, which is meanwhile revised by the global Sharpness Aware Minimization (SAM) optimizer to search for the consistent flat minima. Our theoretical analysis indicates that {\ttfamily FedSMOO} achieves fast $\mathcal{O}(1/T)$ convergence rate with low generalization bound. Extensive numerical studies are conducted on the real-world dataset to verify its peerless efficiency and excellent generality.

Decentralized Weakly Convex Optimization Over the Stiefel Manifold

We focus on a class of non-smooth optimization problems over the Stiefel manifold in the decentralized setting, where a connected network of $n$ agents cooperatively minimize a finite-sum objective function with each component being weakly convex in the ambient Euclidean space. Such optimization problems, albeit frequently encountered in applications, are quite challenging due to their non-smoothness and non-convexity. To tackle them, we propose an iterative method called the decentralized Riemannian subgradient method (DRSM). The global convergence and an iteration complexity of $\mathcal{O}(\varepsilon^{-2} \log^2(\varepsilon^{-1}))$ for forcing a natural stationarity measure below $\varepsilon$ are established via the powerful tool of proximal smoothness from variational analysis, which could be of independent interest. Besides, we show the local linear convergence of the DRSM using geometrically diminishing stepsizes when the problem at hand further possesses a sharpness property. Numerical experiments are conducted to corroborate our theoretical findings.

OmniForce: On Human-Centered, Large Model Empowered and Cloud-Edge Collaborative AutoML System

Automated machine learning (AutoML) seeks to build ML models with minimal human effort. While considerable research has been conducted in the area of AutoML in general, aiming to take humans out of the loop when building artificial intelligence (AI) applications, scant literature has focused on how AutoML works well in open-environment scenarios such as the process of training and updating large models, industrial supply chains or the industrial metaverse, where people often face open-loop problems during the search process: they must continuously collect data, update data and models, satisfy the requirements of the development and deployment environment, support massive devices, modify evaluation metrics, etc. Addressing the open-environment issue with pure data-driven approaches requires considerable data, computing resources, and effort from dedicated data engineers, making current AutoML systems and platforms inefficient and computationally intractable. Human-computer interaction is a practical and feasible way to tackle the problem of open-environment AI. In this paper, we introduce OmniForce, a human-centered AutoML (HAML) system that yields both human-assisted ML and ML-assisted human techniques, to put an AutoML system into practice and build adaptive AI in open-environment scenarios. Specifically, we present OmniForce in terms of ML version management; pipeline-driven development and deployment collaborations; a flexible search strategy framework; and widely provisioned and crowdsourced application algorithms, including large models. Furthermore, the (large) models constructed by OmniForce can be automatically turned into remote services in a few minutes; this process is dubbed model as a service (MaaS). Experimental results obtained in multiple search spaces and real-world use cases demonstrate the efficacy and efficiency of OmniForce.

AdaSAM: Boosting Sharpness-Aware Minimization with Adaptive Learning Rate and Momentum for Training Deep Neural Networks

Sharpness aware minimization (SAM) optimizer has been extensively explored as it can generalize better for training deep neural networks via introducing extra perturbation steps to flatten the landscape of deep learning models. Integrating SAM with adaptive learning rate and momentum acceleration, dubbed AdaSAM, has already been explored empirically to train large-scale deep neural networks without theoretical guarantee due to the triple difficulties in analyzing the coupled perturbation step, adaptive learning rate and momentum step. In this paper, we try to analyze the convergence rate of AdaSAM in the stochastic non-convex setting. We theoretically show that AdaSAM admits a $\mathcal{O}(1/\sqrt{bT})$ convergence rate, which achieves linear speedup property with respect to mini-batch size $b$. Specifically, to decouple the stochastic gradient steps with the adaptive learning rate and perturbed gradient, we introduce the delayed second-order momentum term to decompose them to make them independent while taking an expectation during the analysis. Then we bound them by showing the adaptive learning rate has a limited range, which makes our analysis feasible. To the best of our knowledge, we are the first to provide the non-trivial convergence rate of SAM with an adaptive learning rate and momentum acceleration. At last, we conduct several experiments on several NLP tasks, which show that AdaSAM could achieve superior performance compared with SGD, AMSGrad, and SAM optimizers.

Penalized Proximal Policy Optimization for Safe Reinforcement Learning

Safe reinforcement learning aims to learn the optimal policy while satisfying safety constraints, which is essential in real-world applications. However, current algorithms still struggle for efficient policy updates with hard constraint satisfaction. In this paper, we propose Penalized Proximal Policy Optimization (P3O), which solves the cumbersome constrained policy iteration via a single minimization of an equivalent unconstrained problem. Specifically, P3O utilizes a simple-yet-effective penalty function to eliminate cost constraints and removes the trust-region constraint by the clipped surrogate objective. We theoretically prove the exactness of the proposed method with a finite penalty factor and provide a worst-case analysis for approximate error when evaluated on sample trajectories. Moreover, we extend P3O to more challenging multi-constraint and multi-agent scenarios which are less studied in previous work. Extensive experiments show that P3O outperforms state-of-the-art algorithms with respect to both reward improvement and constraint satisfaction on a set of constrained locomotive tasks.

Do We Really Need a Learnable Classifier at the End of Deep Neural Network?

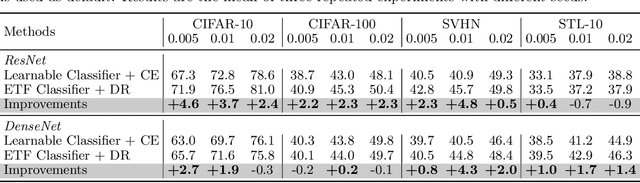
Modern deep neural networks for classification usually jointly learn a backbone for representation and a linear classifier to output the logit of each class. A recent study has shown a phenomenon called neural collapse that the within-class means of features and the classifier vectors converge to the vertices of a simplex equiangular tight frame (ETF) at the terminal phase of training on a balanced dataset. Since the ETF geometric structure maximally separates the pair-wise angles of all classes in the classifier, it is natural to raise the question, why do we spend an effort to learn a classifier when we know its optimal geometric structure? In this paper, we study the potential of learning a neural network for classification with the classifier randomly initialized as an ETF and fixed during training. Our analytical work based on the layer-peeled model indicates that the feature learning with a fixed ETF classifier naturally leads to the neural collapse state even when the dataset is imbalanced among classes. We further show that in this case the cross entropy (CE) loss is not necessary and can be replaced by a simple squared loss that shares the same global optimality but enjoys a more accurate gradient and better convergence property. Our experimental results show that our method is able to achieve similar performances on image classification for balanced datasets, and bring significant improvements in the long-tailed and fine-grained classification tasks.

Decentralized Riemannian Gradient Descent on the Stiefel Manifold

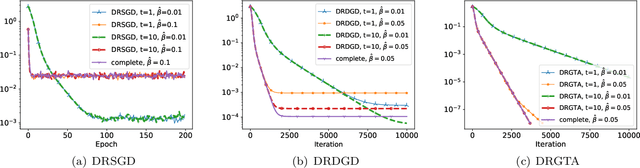
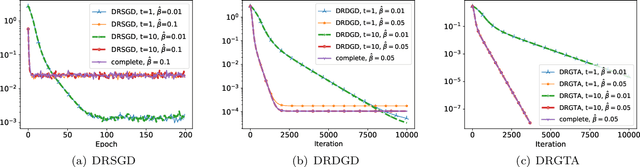
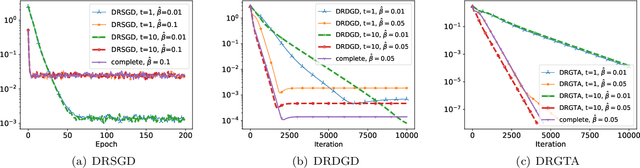
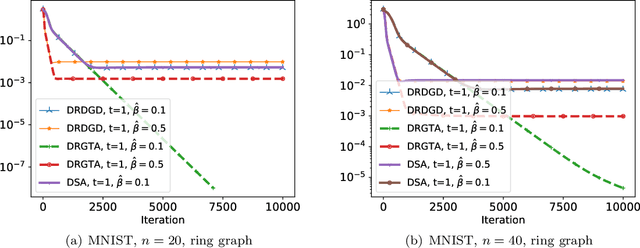
We consider a distributed non-convex optimization where a network of agents aims at minimizing a global function over the Stiefel manifold. The global function is represented as a finite sum of smooth local functions, where each local function is associated with one agent and agents communicate with each other over an undirected connected graph. The problem is non-convex as local functions are possibly non-convex (but smooth) and the Steifel manifold is a non-convex set. We present a decentralized Riemannian stochastic gradient method (DRSGD) with the convergence rate of $\mathcal{O}(1/\sqrt{K})$ to a stationary point. To have exact convergence with constant stepsize, we also propose a decentralized Riemannian gradient tracking algorithm (DRGTA) with the convergence rate of $\mathcal{O}(1/K)$ to a stationary point. We use multi-step consensus to preserve the iteration in the local (consensus) region. DRGTA is the first decentralized algorithm with exact convergence for distributed optimization on Stiefel manifold.