Finite-Time Analysis of Stochastic Nonconvex Nonsmooth Optimization on the Riemannian Manifolds

This work addresses the finite-time analysis of nonsmooth nonconvex stochastic optimization under Riemannian manifold constraints. We adapt the notion of Goldstein stationarity to the Riemannian setting as a performance metric for nonsmooth optimization on manifolds. We then propose a Riemannian Online to NonConvex (RO2NC) algorithm, for which we establish the sample complexity of $O(\epsilon^{-3}\delta^{-1})$ in finding $(\delta,\epsilon)$-stationary points. This result is the first-ever finite-time guarantee for fully nonsmooth, nonconvex optimization on manifolds and matches the optimal complexity in the Euclidean setting. When gradient information is unavailable, we develop a zeroth order version of RO2NC algorithm (ZO-RO2NC), for which we establish the same sample complexity. The numerical results support the theory and demonstrate the practical effectiveness of the algorithms.

FlowRL: Matching Reward Distributions for LLM Reasoning

We propose FlowRL: matching the full reward distribution via flow balancing instead of maximizing rewards in large language model (LLM) reinforcement learning (RL). Recent advanced reasoning models adopt reward-maximizing methods (\eg, PPO and GRPO), which tend to over-optimize dominant reward signals while neglecting less frequent but valid reasoning paths, thus reducing diversity. In contrast, we transform scalar rewards into a normalized target distribution using a learnable partition function, and then minimize the reverse KL divergence between the policy and the target distribution. We implement this idea as a flow-balanced optimization method that promotes diverse exploration and generalizable reasoning trajectories. We conduct experiments on math and code reasoning tasks: FlowRL achieves a significant average improvement of $10.0\%$ over GRPO and $5.1\%$ over PPO on math benchmarks, and performs consistently better on code reasoning tasks. These results highlight reward distribution-matching as a key step toward efficient exploration and diverse reasoning in LLM reinforcement learning.

SimpleVLA-RL: Scaling VLA Training via Reinforcement Learning

Vision-Language-Action (VLA) models have recently emerged as a powerful paradigm for robotic manipulation. Despite substantial progress enabled by large-scale pretraining and supervised fine-tuning (SFT), these models face two fundamental challenges: (i) the scarcity and high cost of large-scale human-operated robotic trajectories required for SFT scaling, and (ii) limited generalization to tasks involving distribution shift. Recent breakthroughs in Large Reasoning Models (LRMs) demonstrate that reinforcement learning (RL) can dramatically enhance step-by-step reasoning capabilities, raising a natural question: Can RL similarly improve the long-horizon step-by-step action planning of VLA? In this work, we introduce SimpleVLA-RL, an efficient RL framework tailored for VLA models. Building upon veRL, we introduce VLA-specific trajectory sampling, scalable parallelization, multi-environment rendering, and optimized loss computation. When applied to OpenVLA-OFT, SimpleVLA-RL achieves SoTA performance on LIBERO and even outperforms $\pi_0$ on RoboTwin 1.0\&2.0 with the exploration-enhancing strategies we introduce. SimpleVLA-RL not only reduces dependence on large-scale data and enables robust generalization, but also remarkably surpasses SFT in real-world tasks. Moreover, we identify a novel phenomenon ``pushcut'' during RL training, wherein the policy discovers previously unseen patterns beyond those seen in the previous training process. Github: https://github.com/PRIME-RL/SimpleVLA-RL

A Survey of Reinforcement Learning for Large Reasoning Models

In this paper, we survey recent advances in Reinforcement Learning (RL) for reasoning with Large Language Models (LLMs). RL has achieved remarkable success in advancing the frontier of LLM capabilities, particularly in addressing complex logical tasks such as mathematics and coding. As a result, RL has emerged as a foundational methodology for transforming LLMs into LRMs. With the rapid progress of the field, further scaling of RL for LRMs now faces foundational challenges not only in computational resources but also in algorithm design, training data, and infrastructure. To this end, it is timely to revisit the development of this domain, reassess its trajectory, and explore strategies to enhance the scalability of RL toward Artificial SuperIntelligence (ASI). In particular, we examine research applying RL to LLMs and LRMs for reasoning abilities, especially since the release of DeepSeek-R1, including foundational components, core problems, training resources, and downstream applications, to identify future opportunities and directions for this rapidly evolving area. We hope this review will promote future research on RL for broader reasoning models. Github: https://github.com/TsinghuaC3I/Awesome-RL-for-LRMs

Towards a Unified View of Large Language Model Post-Training

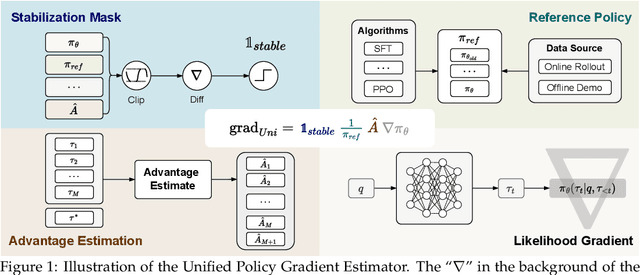
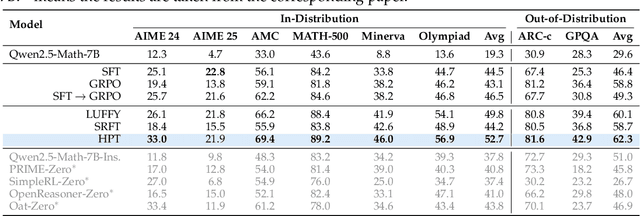
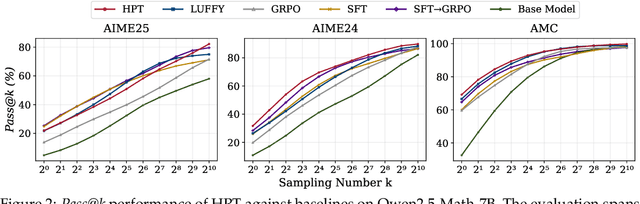
Two major sources of training data exist for post-training modern language models: online (model-generated rollouts) data, and offline (human or other-model demonstrations) data. These two types of data are typically used by approaches like Reinforcement Learning (RL) and Supervised Fine-Tuning (SFT), respectively. In this paper, we show that these approaches are not in contradiction, but are instances of a single optimization process. We derive a Unified Policy Gradient Estimator, and present the calculations of a wide spectrum of post-training approaches as the gradient of a common objective under different data distribution assumptions and various bias-variance tradeoffs. The gradient estimator is constructed with four interchangeable parts: stabilization mask, reference policy denominator, advantage estimate, and likelihood gradient. Motivated by our theoretical findings, we propose Hybrid Post-Training (HPT), an algorithm that dynamically selects different training signals. HPT is designed to yield both effective exploitation of demonstration and stable exploration without sacrificing learned reasoning patterns. We provide extensive experiments and ablation studies to verify the effectiveness of our unified theoretical framework and HPT. Across six mathematical reasoning benchmarks and two out-of-distribution suites, HPT consistently surpasses strong baselines across models of varying scales and families.

Automating Exploratory Multiomics Research via Language Models

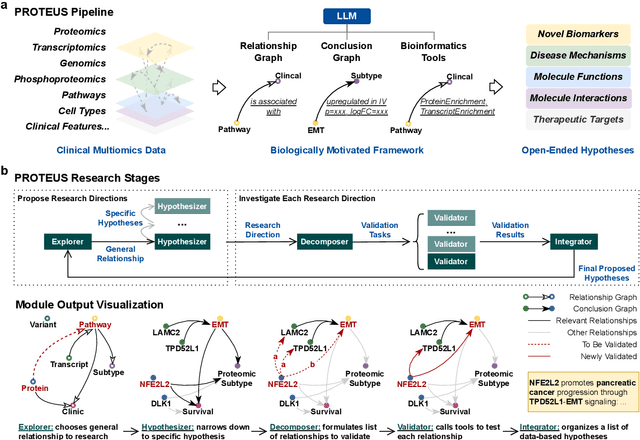
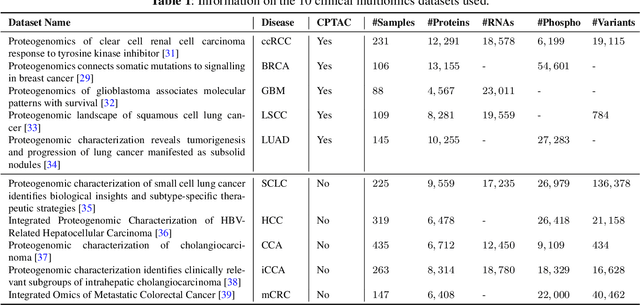
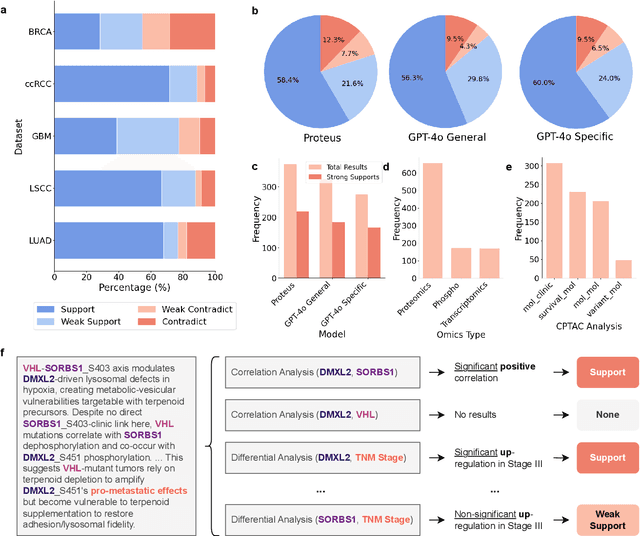
This paper introduces PROTEUS, a fully automated system that produces data-driven hypotheses from raw data files. We apply PROTEUS to clinical proteogenomics, a field where effective downstream data analysis and hypothesis proposal is crucial for producing novel discoveries. PROTEUS uses separate modules to simulate different stages of the scientific process, from open-ended data exploration to specific statistical analysis and hypothesis proposal. It formulates research directions, tools, and results in terms of relationships between biological entities, using unified graph structures to manage complex research processes. We applied PROTEUS to 10 clinical multiomics datasets from published research, arriving at 360 total hypotheses. Results were evaluated through external data validation and automatic open-ended scoring. Through exploratory and iterative research, the system can navigate high-throughput and heterogeneous multiomics data to arrive at hypotheses that balance reliability and novelty. In addition to accelerating multiomic analysis, PROTEUS represents a path towards tailoring general autonomous systems to specialized scientific domains to achieve open-ended hypothesis generation from data.

TTRL: Test-Time Reinforcement Learning

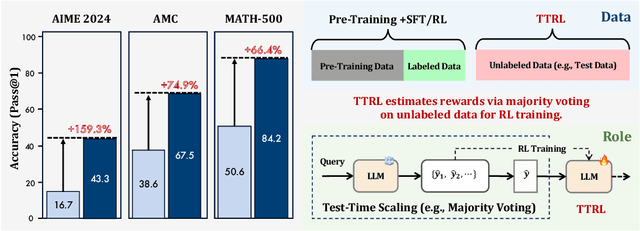
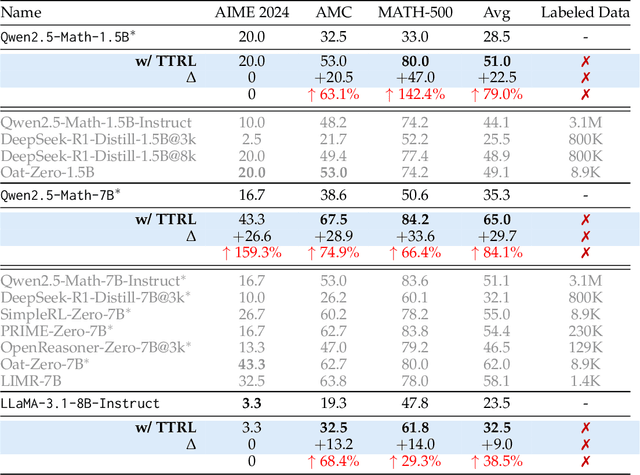
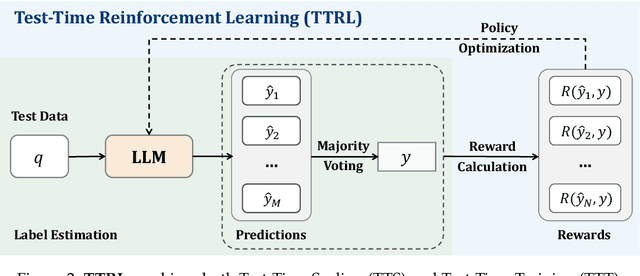
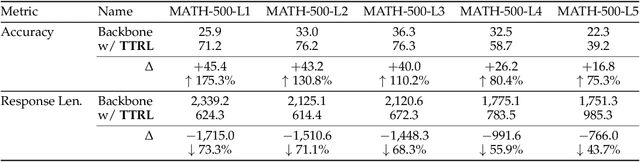
This paper investigates Reinforcement Learning (RL) on data without explicit labels for reasoning tasks in Large Language Models (LLMs). The core challenge of the problem is reward estimation during inference while not having access to ground-truth information. While this setting appears elusive, we find that common practices in Test-Time Scaling (TTS), such as majority voting, yield surprisingly effective rewards suitable for driving RL training. In this work, we introduce Test-Time Reinforcement Learning (TTRL), a novel method for training LLMs using RL on unlabeled data. TTRL enables self-evolution of LLMs by utilizing the priors in the pre-trained models. Our experiments demonstrate that TTRL consistently improves performance across a variety of tasks and models. Notably, TTRL boosts the pass@1 performance of Qwen-2.5-Math-7B by approximately 159% on the AIME 2024 with only unlabeled test data. Furthermore, although TTRL is only supervised by the Maj@N metric, TTRL has demonstrated performance to consistently surpass the upper limit of the initial model, and approach the performance of models trained directly on test data with ground-truth labels. Our experimental findings validate the general effectiveness of TTRL across various tasks, and highlight TTRL's potential for broader tasks and domains. GitHub: https://github.com/PRIME-RL/TTRL

Technologies on Effectiveness and Efficiency: A Survey of State Spaces Models

State Space Models (SSMs) have emerged as a promising alternative to the popular transformer-based models and have been increasingly gaining attention. Compared to transformers, SSMs excel at tasks with sequential data or longer contexts, demonstrating comparable performances with significant efficiency gains. In this survey, we provide a coherent and systematic overview for SSMs, including their theoretical motivations, mathematical formulations, comparison with existing model classes, and various applications. We divide the SSM series into three main sections, providing a detailed introduction to the original SSM, the structured SSM represented by S4, and the selective SSM typified by Mamba. We put an emphasis on technicality, and highlight the various key techniques introduced to address the effectiveness and efficiency of SSMs. We hope this manuscript serves as an introduction for researchers to explore the theoretical foundations of SSMs.

Fourier Position Embedding: Enhancing Attention's Periodic Extension for Length Generalization

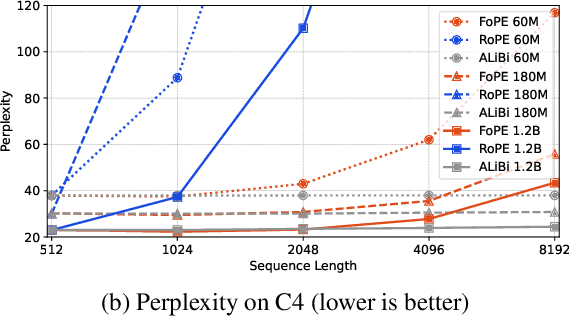
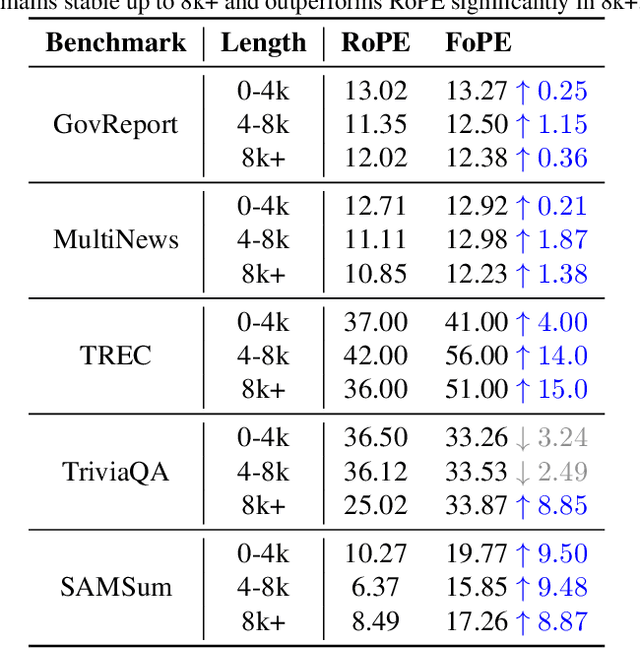
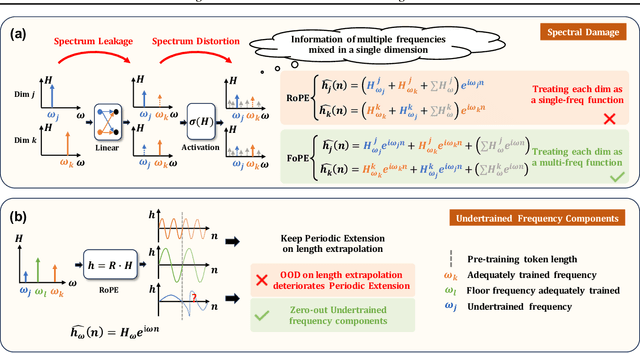
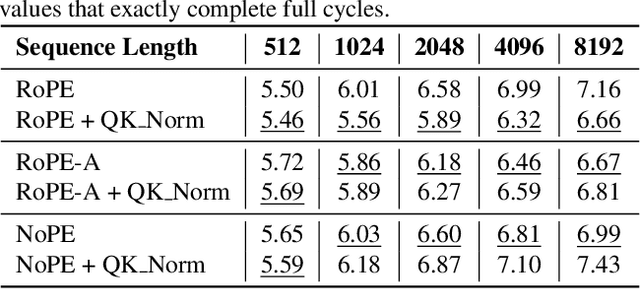
Extending the context length of Language Models (LMs) by improving Rotary Position Embedding (RoPE) has become a trend. While existing works mainly address RoPE's limitations within attention mechanism, this paper provides an analysis across nearly all parts of LMs, uncovering their adverse effects on length generalization for RoPE-based attention. Using Discrete Signal Processing theory, we show that RoPE enables periodic attention by implicitly achieving Non-Uniform Discrete Fourier Transform. However, this periodicity is undermined by the spectral damage caused by: 1) linear layers and activation functions outside of attention; 2) insufficiently trained frequency components brought by time-domain truncation. Building on our observations, we propose Fourier Position Embedding (FoPE), which enhances attention's frequency-domain properties to improve both its periodic extension and length generalization. FoPE constructs Fourier Series and zero-outs the destructive frequency components, increasing model robustness against the spectrum damage. Experiments across various model scales show that, within varying context windows, FoPE can maintain a more stable perplexity and a more consistent accuracy in a needle-in-haystack task compared to RoPE and ALiBi. Several analyses and ablations bring further support to our method and theoretical modeling.

Local Linear Convergence of Infeasible Optimization with Orthogonal Constraints

Many classical and modern machine learning algorithms require solving optimization tasks under orthogonality constraints. Solving these tasks with feasible methods requires a gradient descent update followed by a retraction operation on the Stiefel manifold, which can be computationally expensive. Recently, an infeasible retraction-free approach, termed the landing algorithm, was proposed as an efficient alternative. Motivated by the common occurrence of orthogonality constraints in tasks such as principle component analysis and training of deep neural networks, this paper studies the landing algorithm and establishes a novel linear convergence rate for smooth non-convex functions using only a local Riemannian P{\L} condition. Numerical experiments demonstrate that the landing algorithm performs on par with the state-of-the-art retraction-based methods with substantially reduced computational overhead.