SHAQ: Incorporating Shapley Value Theory into Q-Learning for Multi-Agent Reinforcement Learning
Paper and Code
May 31, 2021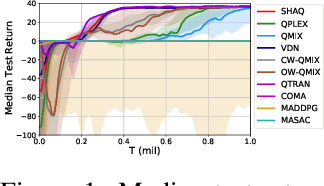

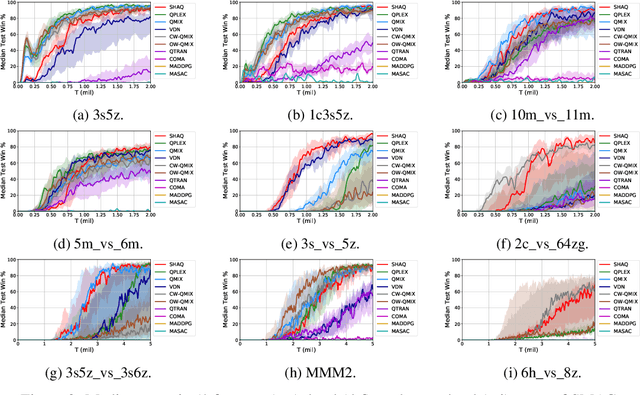
Value factorisation proves to be a very useful technique in multi-agent reinforcement learning (MARL), but the underlying mechanism is not yet fully understood. This paper explores a theoretic basis for value factorisation. We generalise the Shapley value in the coalitional game theory to a Markov convex game (MCG) and use it to guide value factorisation in MARL. We show that the generalised Shapley value possesses several features such as (1) accurate estimation of the maximum global value, (2) fairness in the factorisation of the global value, and (3) being sensitive to dummy agents. The proposed theory yields a new learning algorithm called Sharpley Q-learning (SHAQ), which inherits the important merits of ordinary Q-learning but extends it to MARL. In comparison with prior-arts, SHAQ has a much weaker assumption (MCG) that is more compatible with real-world problems, but has superior explainability and performance in many cases. We demonstrated SHAQ and verified the theoretic claims on Predator-Prey and StarCraft Multi-Agent Challenge (SMAC).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge