A Geometric Unification of Distributionally Robust Covariance Estimators: Shrinking the Spectrum by Inflating the Ambiguity Set

The state-of-the-art methods for estimating high-dimensional covariance matrices all shrink the eigenvalues of the sample covariance matrix towards a data-insensitive shrinkage target. The underlying shrinkage transformation is either chosen heuristically - without compelling theoretical justification - or optimally in view of restrictive distributional assumptions. In this paper, we propose a principled approach to construct covariance estimators without imposing restrictive assumptions. That is, we study distributionally robust covariance estimation problems that minimize the worst-case Frobenius error with respect to all data distributions close to a nominal distribution, where the proximity of distributions is measured via a divergence on the space of covariance matrices. We identify mild conditions on this divergence under which the resulting minimizers represent shrinkage estimators. We show that the corresponding shrinkage transformations are intimately related to the geometrical properties of the underlying divergence. We also prove that our robust estimators are efficiently computable and asymptotically consistent and that they enjoy finite-sample performance guarantees. We exemplify our general methodology by synthesizing explicit estimators induced by the Kullback-Leibler, Fisher-Rao, and Wasserstein divergences. Numerical experiments based on synthetic and real data show that our robust estimators are competitive with state-of-the-art estimators.

End-to-End Learning for Stochastic Optimization: A Bayesian Perspective

We develop a principled approach to end-to-end learning in stochastic optimization. First, we show that the standard end-to-end learning algorithm admits a Bayesian interpretation and trains a posterior Bayes action map. Building on the insights of this analysis, we then propose new end-to-end learning algorithms for training decision maps that output solutions of empirical risk minimization and distributionally robust optimization problems, two dominant modeling paradigms in optimization under uncertainty. Numerical results for a synthetic newsvendor problem illustrate the key differences between alternative training schemes. We also investigate an economic dispatch problem based on real data to showcase the impact of the neural network architecture of the decision maps on their test performance.

Metrizing Fairness

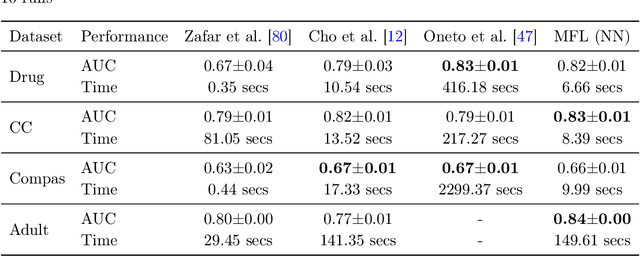
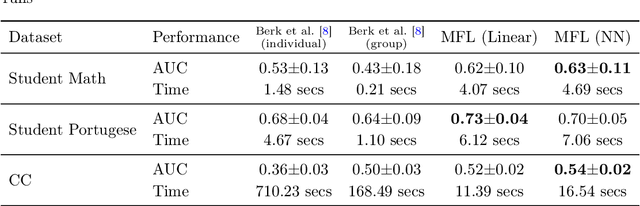
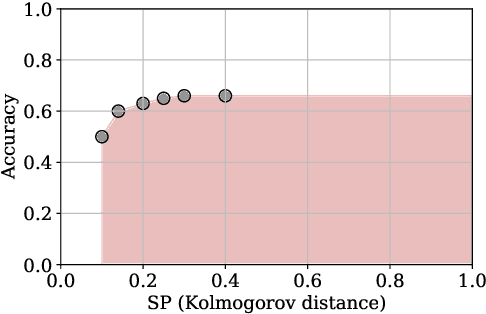
We study supervised learning problems for predicting properties of individuals who belong to one of two demographic groups, and we seek predictors that are fair according to statistical parity. This means that the distributions of the predictions within the two groups should be close with respect to the Kolmogorov distance, and fairness is achieved by penalizing the dissimilarity of these two distributions in the objective function of the learning problem. In this paper, we showcase conceptual and computational benefits of measuring unfairness with integral probability metrics (IPMs) other than the Kolmogorov distance. Conceptually, we show that the generator of any IPM can be interpreted as a family of utility functions and that unfairness with respect to this IPM arises if individuals in the two demographic groups have diverging expected utilities. We also prove that the unfairness-regularized prediction loss admits unbiased gradient estimators if unfairness is measured by the squared $\mathcal L^2$-distance or by a squared maximum mean discrepancy. In this case, the fair learning problem is susceptible to efficient stochastic gradient descent (SGD) algorithms. Numerical experiments on real data show that these SGD algorithms outperform state-of-the-art methods for fair learning in that they achieve superior accuracy-unfairness trade-offs -- sometimes orders of magnitude faster. Finally, we identify conditions under which statistical parity can improve prediction accuracy.

QUACKIE: A NLP Classification Task With Ground Truth Explanations

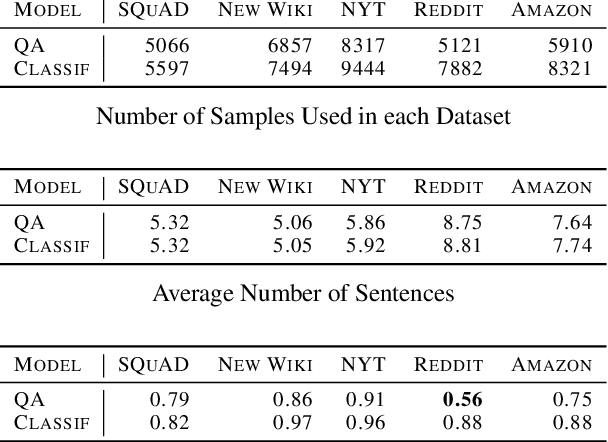
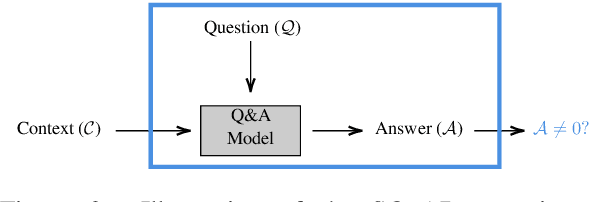
NLP Interpretability aims to increase trust in model predictions. This makes evaluating interpretability approaches a pressing issue. There are multiple datasets for evaluating NLP Interpretability, but their dependence on human provided ground truths raises questions about their unbiasedness. In this work, we take a different approach and formulate a specific classification task by diverting question-answering datasets. For this custom classification task, the interpretability ground-truth arises directly from the definition of the classification problem. We use this method to propose a benchmark and lay the groundwork for future research in NLP interpretability by evaluating a wide range of current state of the art methods.

Sentence-Based Model Agnostic NLP Interpretability

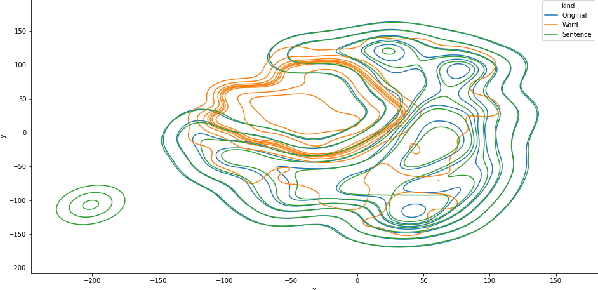
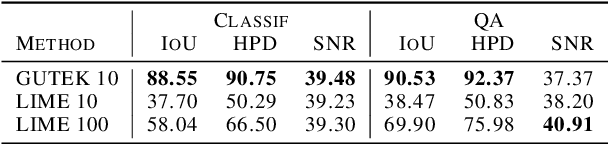
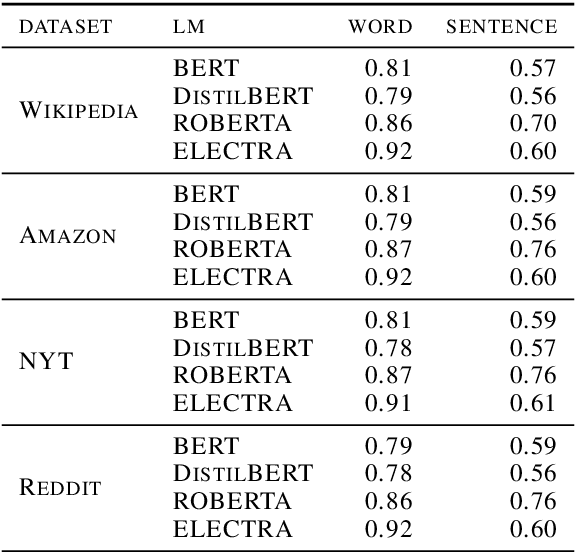
Today, interpretability of Black-Box Natural Language Processing (NLP) models based on surrogates, like LIME or SHAP, uses word-based sampling to build the explanations. In this paper we explore the use of sentences to tackle NLP interpretability. While this choice may seem straight forward, we show that, when using complex classifiers like BERT, the word-based approach raises issues not only of computational complexity, but also of an out of distribution sampling, eventually leading to non founded explanations. By using sentences, the altered text remains in-distribution and the dimensionality of the problem is reduced for better fidelity to the black-box at comparable computational complexity.