Optimism in the Face of Ambiguity Principle for Multi-Armed Bandits

Follow-The-Regularized-Leader (FTRL) algorithms often enjoy optimal regret for adversarial as well as stochastic bandit problems and allow for a streamlined analysis. Nonetheless, FTRL algorithms require the solution of an optimization problem in every iteration and are thus computationally challenging. In contrast, Follow-The-Perturbed-Leader (FTPL) algorithms achieve computational efficiency by perturbing the estimates of the rewards of the arms, but their regret analysis is cumbersome. We propose a new FTPL algorithm that generates optimal policies for both adversarial and stochastic multi-armed bandits. Like FTRL, our algorithm admits a unified regret analysis, and similar to FTPL, it offers low computational costs. Unlike existing FTPL algorithms that rely on independent additive disturbances governed by a \textit{known} distribution, we allow for disturbances governed by an \textit{ambiguous} distribution that is only known to belong to a given set and propose a principle of optimism in the face of ambiguity. Consequently, our framework generalizes existing FTPL algorithms. It also encapsulates a broad range of FTRL methods as special cases, including several optimal ones, which appears to be impossible with current FTPL methods. Finally, we use techniques from discrete choice theory to devise an efficient bisection algorithm for computing the optimistic arm sampling probabilities. This algorithm is up to $10^4$ times faster than standard FTRL algorithms that solve an optimization problem in every iteration. Our results not only settle existing conjectures but also provide new insights into the impact of perturbations by mapping FTRL to FTPL.

Unifying Distributionally Robust Optimization via Optimal Transport Theory

In the past few years, there has been considerable interest in two prominent approaches for Distributionally Robust Optimization (DRO): Divergence-based and Wasserstein-based methods. The divergence approach models misspecification in terms of likelihood ratios, while the latter models it through a measure of distance or cost in actual outcomes. Building upon these advances, this paper introduces a novel approach that unifies these methods into a single framework based on optimal transport (OT) with conditional moment constraints. Our proposed approach, for example, makes it possible for optimal adversarial distributions to simultaneously perturb likelihood and outcomes, while producing an optimal (in an optimal transport sense) coupling between the baseline model and the adversarial model.Additionally, the paper investigates several duality results and presents tractable reformulations that enhance the practical applicability of this unified framework.

Metrizing Fairness

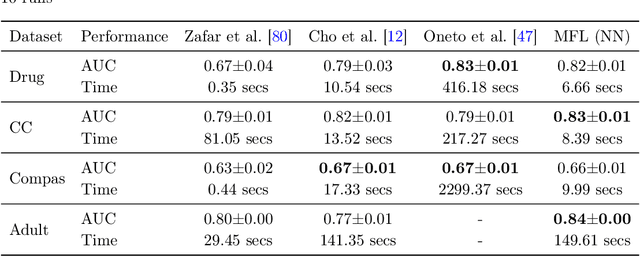
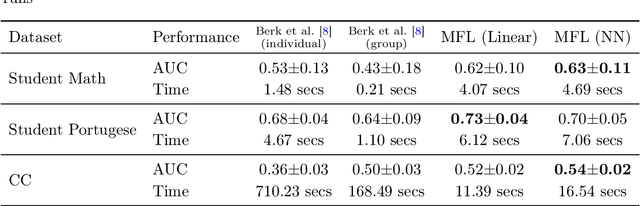
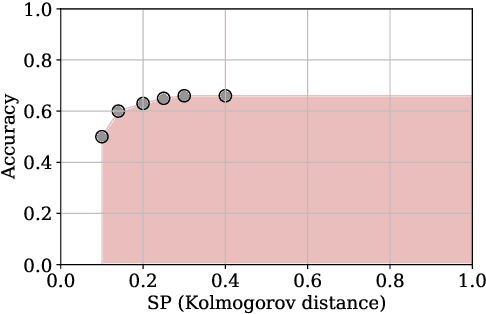
We study supervised learning problems for predicting properties of individuals who belong to one of two demographic groups, and we seek predictors that are fair according to statistical parity. This means that the distributions of the predictions within the two groups should be close with respect to the Kolmogorov distance, and fairness is achieved by penalizing the dissimilarity of these two distributions in the objective function of the learning problem. In this paper, we showcase conceptual and computational benefits of measuring unfairness with integral probability metrics (IPMs) other than the Kolmogorov distance. Conceptually, we show that the generator of any IPM can be interpreted as a family of utility functions and that unfairness with respect to this IPM arises if individuals in the two demographic groups have diverging expected utilities. We also prove that the unfairness-regularized prediction loss admits unbiased gradient estimators if unfairness is measured by the squared $\mathcal L^2$-distance or by a squared maximum mean discrepancy. In this case, the fair learning problem is susceptible to efficient stochastic gradient descent (SGD) algorithms. Numerical experiments on real data show that these SGD algorithms outperform state-of-the-art methods for fair learning in that they achieve superior accuracy-unfairness trade-offs -- sometimes orders of magnitude faster. Finally, we identify conditions under which statistical parity can improve prediction accuracy.

Sequential Domain Adaptation by Synthesizing Distributionally Robust Experts

Least squares estimators, when trained on a few target domain samples, may predict poorly. Supervised domain adaptation aims to improve the predictive accuracy by exploiting additional labeled training samples from a source distribution that is close to the target distribution. Given available data, we investigate novel strategies to synthesize a family of least squares estimator experts that are robust with regard to moment conditions. When these moment conditions are specified using Kullback-Leibler or Wasserstein-type divergences, we can find the robust estimators efficiently using convex optimization. We use the Bernstein online aggregation algorithm on the proposed family of robust experts to generate predictions for the sequential stream of target test samples. Numerical experiments on real data show that the robust strategies may outperform non-robust interpolations of the empirical least squares estimators.

Semi-Discrete Optimal Transport: Hardness, Regularization and Numerical Solution

Semi-discrete optimal transport problems, which evaluate the Wasserstein distance between a discrete and a generic (possibly non-discrete) probability measure, are believed to be computationally hard. Even though such problems are ubiquitous in statistics, machine learning and computer vision, however, this perception has not yet received a theoretical justification. To fill this gap, we prove that computing the Wasserstein distance between a discrete probability measure supported on two points and the Lebesgue measure on the standard hypercube is already #P-hard. This insight prompts us to seek approximate solutions for semi-discrete optimal transport problems. We thus perturb the underlying transportation cost with an additive disturbance governed by an ambiguous probability distribution, and we introduce a distributionally robust dual optimal transport problem whose objective function is smoothed with the most adverse disturbance distributions from within a given ambiguity set. We further show that smoothing the dual objective function is equivalent to regularizing the primal objective function, and we identify several ambiguity sets that give rise to several known and new regularization schemes. As a byproduct, we discover an intimate relation between semi-discrete optimal transport problems and discrete choice models traditionally studied in psychology and economics. To solve the regularized optimal transport problems efficiently, we use a stochastic gradient descent algorithm with imprecise stochastic gradient oracles. A new convergence analysis reveals that this algorithm improves the best known convergence guarantee for semi-discrete optimal transport problems with entropic regularizers.

A Statistical Test for Probabilistic Fairness

Algorithms are now routinely used to make consequential decisions that affect human lives. Examples include college admissions, medical interventions or law enforcement. While algorithms empower us to harness all information hidden in vast amounts of data, they may inadvertently amplify existing biases in the available datasets. This concern has sparked increasing interest in fair machine learning, which aims to quantify and mitigate algorithmic discrimination. Indeed, machine learning models should undergo intensive tests to detect algorithmic biases before being deployed at scale. In this paper, we use ideas from the theory of optimal transport to propose a statistical hypothesis test for detecting unfair classifiers. Leveraging the geometry of the feature space, the test statistic quantifies the distance of the empirical distribution supported on the test samples to the manifold of distributions that render a pre-trained classifier fair. We develop a rigorous hypothesis testing mechanism for assessing the probabilistic fairness of any pre-trained logistic classifier, and we show both theoretically as well as empirically that the proposed test is asymptotically correct. In addition, the proposed framework offers interpretability by identifying the most favorable perturbation of the data so that the given classifier becomes fair.

A Distributionally Robust Approach to Fair Classification

We propose a distributionally robust logistic regression model with an unfairness penalty that prevents discrimination with respect to sensitive attributes such as gender or ethnicity. This model is equivalent to a tractable convex optimization problem if a Wasserstein ball centered at the empirical distribution on the training data is used to model distributional uncertainty and if a new convex unfairness measure is used to incentivize equalized opportunities. We demonstrate that the resulting classifier improves fairness at a marginal loss of predictive accuracy on both synthetic and real datasets. We also derive linear programming-based confidence bounds on the level of unfairness of any pre-trained classifier by leveraging techniques from optimal uncertainty quantification over Wasserstein balls.