Ngoc Bui
Hyperbolic Deep Learning for Foundation Models: A Survey
Jul 23, 2025Abstract:Foundation models pre-trained on massive datasets, including large language models (LLMs), vision-language models (VLMs), and large multimodal models, have demonstrated remarkable success in diverse downstream tasks. However, recent studies have shown fundamental limitations of these models: (1) limited representational capacity, (2) lower adaptability, and (3) diminishing scalability. These shortcomings raise a critical question: is Euclidean geometry truly the optimal inductive bias for all foundation models, or could incorporating alternative geometric spaces enable models to better align with the intrinsic structure of real-world data and improve reasoning processes? Hyperbolic spaces, a class of non-Euclidean manifolds characterized by exponential volume growth with respect to distance, offer a mathematically grounded solution. These spaces enable low-distortion embeddings of hierarchical structures (e.g., trees, taxonomies) and power-law distributions with substantially fewer dimensions compared to Euclidean counterparts. Recent advances have leveraged these properties to enhance foundation models, including improving LLMs' complex reasoning ability, VLMs' zero-shot generalization, and cross-modal semantic alignment, while maintaining parameter efficiency. This paper provides a comprehensive review of hyperbolic neural networks and their recent development for foundation models. We further outline key challenges and research directions to advance the field.
Learning Along the Arrow of Time: Hyperbolic Geometry for Backward-Compatible Representation Learning
Jun 06, 2025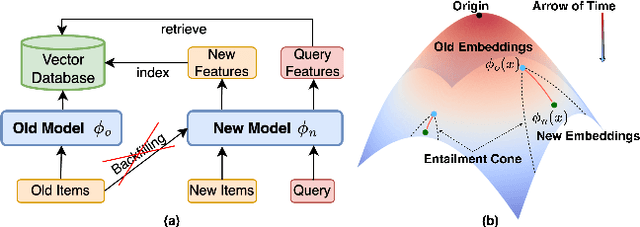
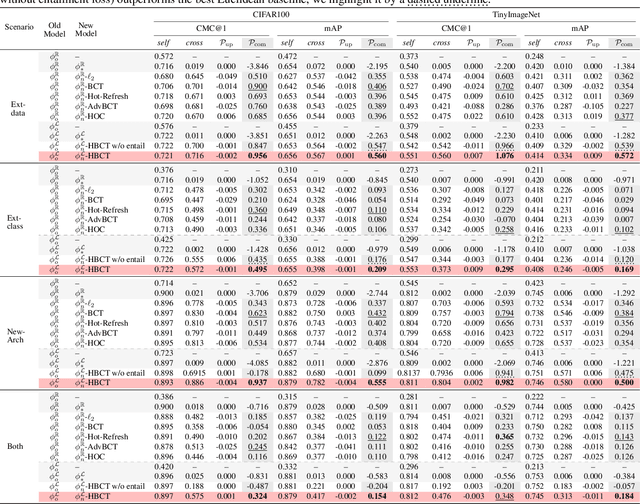
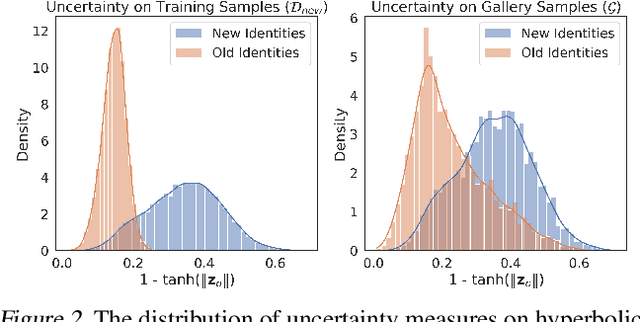
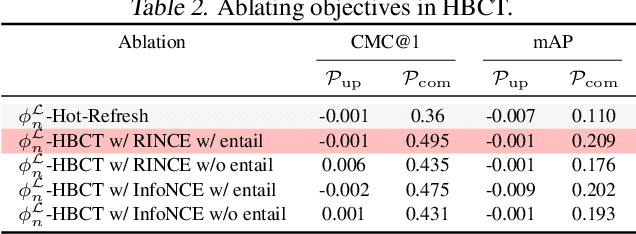
Abstract:Backward compatible representation learning enables updated models to integrate seamlessly with existing ones, avoiding to reprocess stored data. Despite recent advances, existing compatibility approaches in Euclidean space neglect the uncertainty in the old embedding model and force the new model to reconstruct outdated representations regardless of their quality, thereby hindering the learning process of the new model. In this paper, we propose to switch perspectives to hyperbolic geometry, where we treat time as a natural axis for capturing a model's confidence and evolution. By lifting embeddings into hyperbolic space and constraining updated embeddings to lie within the entailment cone of the old ones, we maintain generational consistency across models while accounting for uncertainties in the representations. To further enhance compatibility, we introduce a robust contrastive alignment loss that dynamically adjusts alignment weights based on the uncertainty of the old embeddings. Experiments validate the superiority of the proposed method in achieving compatibility, paving the way for more resilient and adaptable machine learning systems.
Position: Beyond Euclidean -- Foundation Models Should Embrace Non-Euclidean Geometries
Apr 11, 2025Abstract:In the era of foundation models and Large Language Models (LLMs), Euclidean space has been the de facto geometric setting for machine learning architectures. However, recent literature has demonstrated that this choice comes with fundamental limitations. At a large scale, real-world data often exhibit inherently non-Euclidean structures, such as multi-way relationships, hierarchies, symmetries, and non-isotropic scaling, in a variety of domains, such as languages, vision, and the natural sciences. It is challenging to effectively capture these structures within the constraints of Euclidean spaces. This position paper argues that moving beyond Euclidean geometry is not merely an optional enhancement but a necessity to maintain the scaling law for the next-generation of foundation models. By adopting these geometries, foundation models could more efficiently leverage the aforementioned structures. Task-aware adaptability that dynamically reconfigures embeddings to match the geometry of downstream applications could further enhance efficiency and expressivity. Our position is supported by a series of theoretical and empirical investigations of prevalent foundation models.Finally, we outline a roadmap for integrating non-Euclidean geometries into foundation models, including strategies for building geometric foundation models via fine-tuning, training from scratch, and hybrid approaches.
Mixture-of-Personas Language Models for Population Simulation
Apr 07, 2025


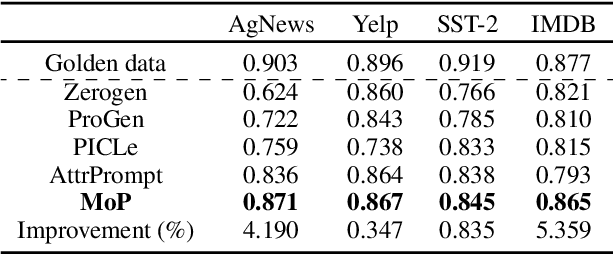
Abstract:Advances in Large Language Models (LLMs) paved the way for their emerging applications in various domains, such as human behavior simulations, where LLMs could augment human-generated data in social science research and machine learning model training. However, pretrained LLMs often fail to capture the behavioral diversity of target populations due to the inherent variability across individuals and groups. To address this, we propose \textit{Mixture of Personas} (MoP), a \textit{probabilistic} prompting method that aligns the LLM responses with the target population. MoP is a contextual mixture model, where each component is an LM agent characterized by a persona and an exemplar representing subpopulation behaviors. The persona and exemplar are randomly chosen according to the learned mixing weights to elicit diverse LLM responses during simulation. MoP is flexible, requires no model finetuning, and is transferable across base models. Experiments for synthetic data generation show that MoP outperforms competing methods in alignment and diversity metrics.
Enhancing Item Tokenization for Generative Recommendation through Self-Improvement
Dec 22, 2024



Abstract:Generative recommendation systems, driven by large language models (LLMs), present an innovative approach to predicting user preferences by modeling items as token sequences and generating recommendations in a generative manner. A critical challenge in this approach is the effective tokenization of items, ensuring that they are represented in a form compatible with LLMs. Current item tokenization methods include using text descriptions, numerical strings, or sequences of discrete tokens. While text-based representations integrate seamlessly with LLM tokenization, they are often too lengthy, leading to inefficiencies and complicating accurate generation. Numerical strings, while concise, lack semantic depth and fail to capture meaningful item relationships. Tokenizing items as sequences of newly defined tokens has gained traction, but it often requires external models or algorithms for token assignment. These external processes may not align with the LLM's internal pretrained tokenization schema, leading to inconsistencies and reduced model performance. To address these limitations, we propose a self-improving item tokenization method that allows the LLM to refine its own item tokenizations during training process. Our approach starts with item tokenizations generated by any external model and periodically adjusts these tokenizations based on the LLM's learned patterns. Such alignment process ensures consistency between the tokenization and the LLM's internal understanding of the items, leading to more accurate recommendations. Furthermore, our method is simple to implement and can be integrated as a plug-and-play enhancement into existing generative recommendation systems. Experimental results on multiple datasets and using various initial tokenization strategies demonstrate the effectiveness of our method, with an average improvement of 8\% in recommendation performance.
Explaining Graph Neural Networks via Structure-aware Interaction Index
May 23, 2024



Abstract:The Shapley value is a prominent tool for interpreting black-box machine learning models thanks to its strong theoretical foundation. However, for models with structured inputs, such as graph neural networks, existing Shapley-based explainability approaches either focus solely on node-wise importance or neglect the graph structure when perturbing the input instance. This paper introduces the Myerson-Taylor interaction index that internalizes the graph structure into attributing the node values and the interaction values among nodes. Unlike the Shapley-based methods, the Myerson-Taylor index decomposes coalitions into components satisfying a pre-chosen connectivity criterion. We prove that the Myerson-Taylor index is the unique one that satisfies a system of five natural axioms accounting for graph structure and high-order interaction among nodes. Leveraging these properties, we propose Myerson-Taylor Structure-Aware Graph Explainer (MAGE), a novel explainer that uses the second-order Myerson-Taylor index to identify the most important motifs influencing the model prediction, both positively and negatively. Extensive experiments on various graph datasets and models demonstrate that our method consistently provides superior subgraph explanations compared to state-of-the-art methods.
Coverage-Validity-Aware Algorithmic Recourse
Nov 19, 2023



Abstract:Algorithmic recourse emerges as a prominent technique to promote the explainability, transparency and hence ethics of machine learning models. Existing algorithmic recourse approaches often assume an invariant predictive model; however, the predictive model is usually updated upon the arrival of new data. Thus, a recourse that is valid respective to the present model may become invalid for the future model. To resolve this issue, we propose a novel framework to generate a model-agnostic recourse that exhibits robustness to model shifts. Our framework first builds a coverage-validity-aware linear surrogate of the nonlinear (black-box) model; then, the recourse is generated with respect to the linear surrogate. We establish a theoretical connection between our coverage-validity-aware linear surrogate and the minimax probability machines (MPM). We then prove that by prescribing different covariance robustness, the proposed framework recovers popular regularizations for MPM, including the $\ell_2$-regularization and class-reweighting. Furthermore, we show that our surrogate pushes the approximate hyperplane intuitively, facilitating not only robust but also interpretable recourses. The numerical results demonstrate the usefulness and robustness of our framework.
Feasible Recourse Plan via Diverse Interpolation
Feb 22, 2023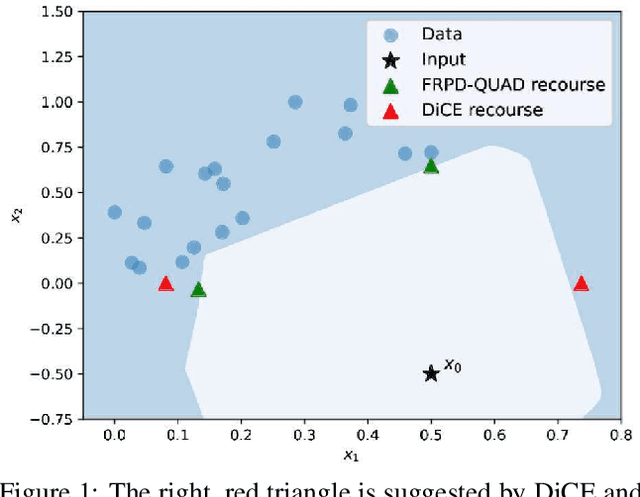
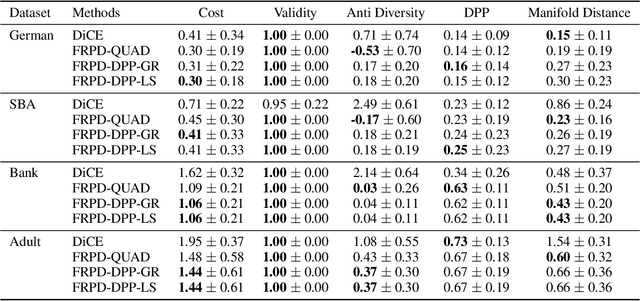
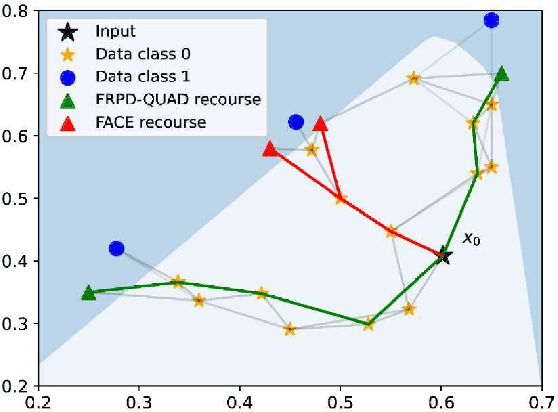
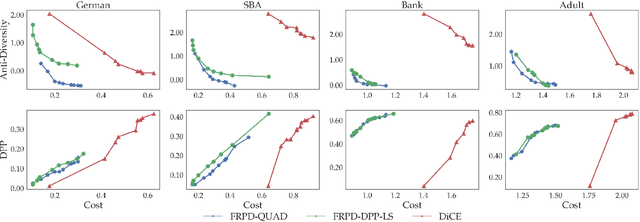
Abstract:Explaining algorithmic decisions and recommending actionable feedback is increasingly important for machine learning applications. Recently, significant efforts have been invested in finding a diverse set of recourses to cover the wide spectrum of users' preferences. However, existing works often neglect the requirement that the recourses should be close to the data manifold; hence, the constructed recourses might be implausible and unsatisfying to users. To address these issues, we propose a novel approach that explicitly directs the diverse set of actionable recourses towards the data manifold. We first find a diverse set of prototypes in the favorable class that balances the trade-off between diversity and proximity. We demonstrate two specific methods to find these prototypes: either by finding the maximum a posteriori estimate of a determinantal point process or by solving a quadratic binary program. To ensure the actionability constraints, we construct an actionability graph in which the nodes represent the training samples and the edges indicate the feasible action between two instances. We then find a feasible path to each prototype, and this path demonstrates the feasible actions for each recourse in the plan. The experimental results show that our method produces a set of recourses that are close to the data manifold while delivering a better cost-diversity trade-off than existing approaches.
Distributionally Robust Recourse Action
Feb 22, 2023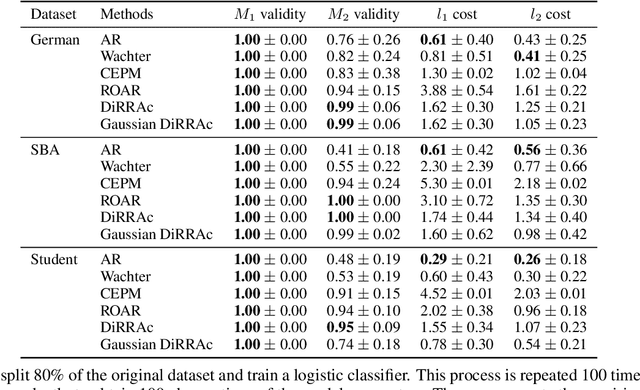

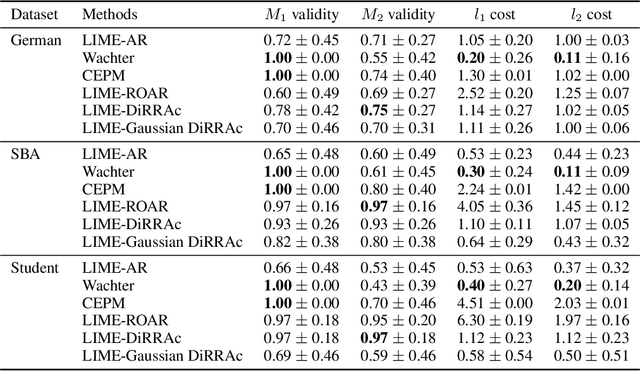

Abstract:A recourse action aims to explain a particular algorithmic decision by showing one specific way in which the instance could be modified to receive an alternate outcome. Existing recourse generation methods often assume that the machine learning model does not change over time. However, this assumption does not always hold in practice because of data distribution shifts, and in this case, the recourse action may become invalid. To redress this shortcoming, we propose the Distributionally Robust Recourse Action (DiRRAc) framework, which generates a recourse action that has a high probability of being valid under a mixture of model shifts. We formulate the robustified recourse setup as a min-max optimization problem, where the max problem is specified by Gelbrich distance over an ambiguity set around the distribution of model parameters. Then we suggest a projected gradient descent algorithm to find a robust recourse according to the min-max objective. We show that our DiRRAc framework can be extended to hedge against the misspecification of the mixture weights. Numerical experiments with both synthetic and three real-world datasets demonstrate the benefits of our proposed framework over state-of-the-art recourse methods.
A Deep Reinforcement Learning-based Adaptive Charging Policy for Wireless Rechargeable Sensor Networks
Aug 16, 2022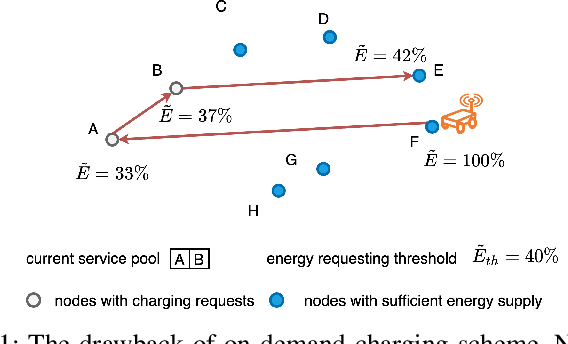
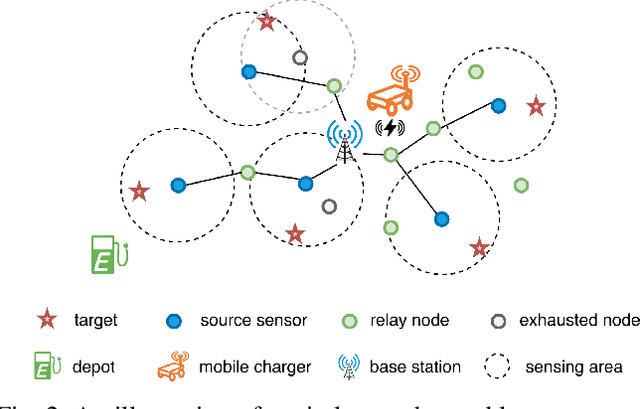


Abstract:Wireless sensor networks consist of randomly distributed sensor nodes for monitoring targets or areas of interest. Maintaining the network for continuous surveillance is a challenge due to the limited battery capacity in each sensor. Wireless power transfer technology is emerging as a reliable solution for energizing the sensors by deploying a mobile charger (MC) to recharge the sensor. However, designing an optimal charging path for the MC is challenging because of uncertainties arising in the networks. The energy consumption rate of the sensors may fluctuate significantly due to unpredictable changes in the network topology, such as node failures. These changes also lead to shifts in the importance of each sensor, which are often assumed to be the same in existing works. We address these challenges in this paper by proposing a novel adaptive charging scheme using a deep reinforcement learning (DRL) approach. Specifically, we endow the MC with a charging policy that determines the next sensor to charge conditioning on the current state of the network. We then use a deep neural network to parametrize this charging policy, which will be trained by reinforcement learning techniques. Our model can adapt to spontaneous changes in the network topology. The empirical results show that the proposed algorithm outperforms the existing on-demand algorithms by a significant margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge