Efficient Identity and Position Graph Embedding via Spectral-Based Random Feature Aggregation

Graph neural networks (GNNs), which capture graph structures via a feature aggregation mechanism following the graph embedding framework, have demonstrated a powerful ability to support various tasks. According to the topology properties (e.g., structural roles or community memberships of nodes) to be preserved, graph embedding can be categorized into identity and position embedding. However, it is unclear for most GNN-based methods which property they can capture. Some of them may also suffer from low efficiency and scalability caused by several time- and space-consuming procedures (e.g., feature extraction and training). From a perspective of graph signal processing, we find that high- and low-frequency information in the graph spectral domain may characterize node identities and positions, respectively. Based on this investigation, we propose random feature aggregation (RFA) for efficient identity and position embedding, serving as an extreme ablation study regarding GNN feature aggregation. RFA (i) adopts a spectral-based GNN without learnable parameters as its backbone, (ii) only uses random noises as inputs, and (iii) derives embeddings via just one feed-forward propagation (FFP). Inspired by degree-corrected spectral clustering, we further introduce a degree correction mechanism to the GNN backbone. Surprisingly, our experiments demonstrate that two variants of RFA with high- and low-pass filters can respectively derive informative identity and position embeddings via just one FFP (i.e., without any training). As a result, RFA can achieve a better trade-off between quality and efficiency for both identity and position embedding over various baselines.

CLIP-Powered Domain Generalization and Domain Adaptation: A Comprehensive Survey

As machine learning evolves, domain generalization (DG) and domain adaptation (DA) have become crucial for enhancing model robustness across diverse environments. Contrastive Language-Image Pretraining (CLIP) plays a significant role in these tasks, offering powerful zero-shot capabilities that allow models to perform effectively in unseen domains. However, there remains a significant gap in the literature, as no comprehensive survey currently exists that systematically explores the applications of CLIP in DG and DA, highlighting the necessity for this review. This survey presents a comprehensive review of CLIP's applications in DG and DA. In DG, we categorize methods into optimizing prompt learning for task alignment and leveraging CLIP as a backbone for effective feature extraction, both enhancing model adaptability. For DA, we examine both source-available methods utilizing labeled source data and source-free approaches primarily based on target domain data, emphasizing knowledge transfer mechanisms and strategies for improved performance across diverse contexts. Key challenges, including overfitting, domain diversity, and computational efficiency, are addressed, alongside future research opportunities to advance robustness and efficiency in practical applications. By synthesizing existing literature and pinpointing critical gaps, this survey provides valuable insights for researchers and practitioners, proposing directions for effectively leveraging CLIP to enhance methodologies in domain generalization and adaptation. Ultimately, this work aims to foster innovation and collaboration in the quest for more resilient machine learning models that can perform reliably across diverse real-world scenarios. A more up-to-date version of the papers is maintained at: https://github.com/jindongli-Ai/Survey_on_CLIP-Powered_Domain_Generalization_and_Adaptation.

Position: Beyond Euclidean -- Foundation Models Should Embrace Non-Euclidean Geometries

In the era of foundation models and Large Language Models (LLMs), Euclidean space has been the de facto geometric setting for machine learning architectures. However, recent literature has demonstrated that this choice comes with fundamental limitations. At a large scale, real-world data often exhibit inherently non-Euclidean structures, such as multi-way relationships, hierarchies, symmetries, and non-isotropic scaling, in a variety of domains, such as languages, vision, and the natural sciences. It is challenging to effectively capture these structures within the constraints of Euclidean spaces. This position paper argues that moving beyond Euclidean geometry is not merely an optional enhancement but a necessity to maintain the scaling law for the next-generation of foundation models. By adopting these geometries, foundation models could more efficiently leverage the aforementioned structures. Task-aware adaptability that dynamically reconfigures embeddings to match the geometry of downstream applications could further enhance efficiency and expressivity. Our position is supported by a series of theoretical and empirical investigations of prevalent foundation models.Finally, we outline a roadmap for integrating non-Euclidean geometries into foundation models, including strategies for building geometric foundation models via fine-tuning, training from scratch, and hybrid approaches.

Step-Audio: Unified Understanding and Generation in Intelligent Speech Interaction

Real-time speech interaction, serving as a fundamental interface for human-machine collaboration, holds immense potential. However, current open-source models face limitations such as high costs in voice data collection, weakness in dynamic control, and limited intelligence. To address these challenges, this paper introduces Step-Audio, the first production-ready open-source solution. Key contributions include: 1) a 130B-parameter unified speech-text multi-modal model that achieves unified understanding and generation, with the Step-Audio-Chat version open-sourced; 2) a generative speech data engine that establishes an affordable voice cloning framework and produces the open-sourced lightweight Step-Audio-TTS-3B model through distillation; 3) an instruction-driven fine control system enabling dynamic adjustments across dialects, emotions, singing, and RAP; 4) an enhanced cognitive architecture augmented with tool calling and role-playing abilities to manage complex tasks effectively. Based on our new StepEval-Audio-360 evaluation benchmark, Step-Audio achieves state-of-the-art performance in human evaluations, especially in terms of instruction following. On open-source benchmarks like LLaMA Question, shows 9.3% average performance improvement, demonstrating our commitment to advancing the development of open-source multi-modal language technologies. Our code and models are available at https://github.com/stepfun-ai/Step-Audio.

A Survey of Personalized Large Language Models: Progress and Future Directions

Large Language Models (LLMs) excel in handling general knowledge tasks, yet they struggle with user-specific personalization, such as understanding individual emotions, writing styles, and preferences. Personalized Large Language Models (PLLMs) tackle these challenges by leveraging individual user data, such as user profiles, historical dialogues, content, and interactions, to deliver responses that are contextually relevant and tailored to each user's specific needs. This is a highly valuable research topic, as PLLMs can significantly enhance user satisfaction and have broad applications in conversational agents, recommendation systems, emotion recognition, medical assistants, and more. This survey reviews recent advancements in PLLMs from three technical perspectives: prompting for personalized context (input level), finetuning for personalized adapters (model level), and alignment for personalized preferences (objective level). To provide deeper insights, we also discuss current limitations and outline several promising directions for future research. Updated information about this survey can be found at the https://github.com/JiahongLiu21/Awesome-Personalized-Large-Language-Models.

Low-Rank Adaptation for Foundation Models: A Comprehensive Review

The rapid advancement of foundation modelslarge-scale neural networks trained on diverse, extensive datasetshas revolutionized artificial intelligence, enabling unprecedented advancements across domains such as natural language processing, computer vision, and scientific discovery. However, the substantial parameter count of these models, often reaching billions or trillions, poses significant challenges in adapting them to specific downstream tasks. Low-Rank Adaptation (LoRA) has emerged as a highly promising approach for mitigating these challenges, offering a parameter-efficient mechanism to fine-tune foundation models with minimal computational overhead. This survey provides the first comprehensive review of LoRA techniques beyond large Language Models to general foundation models, including recent techniques foundations, emerging frontiers and applications of low-rank adaptation across multiple domains. Finally, this survey discusses key challenges and future research directions in theoretical understanding, scalability, and robustness. This survey serves as a valuable resource for researchers and practitioners working with efficient foundation model adaptation.

HC-GLAD: Dual Hyperbolic Contrastive Learning for Unsupervised Graph-Level Anomaly Detection

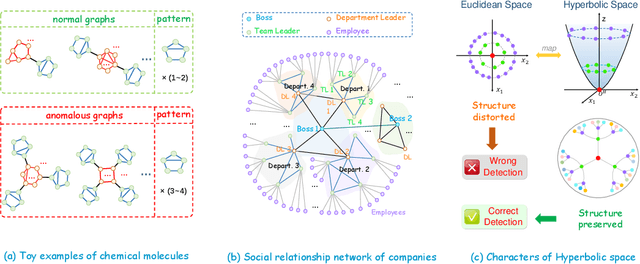
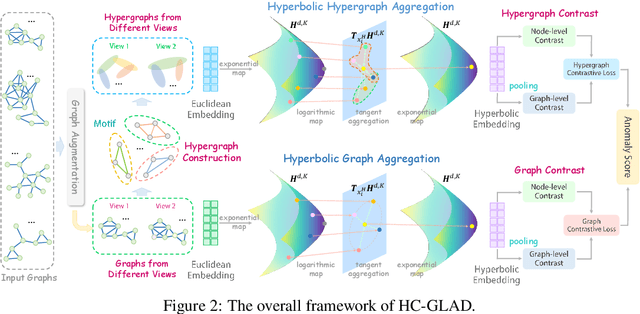
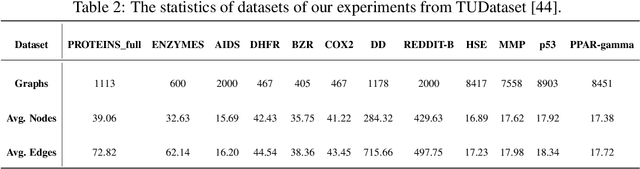
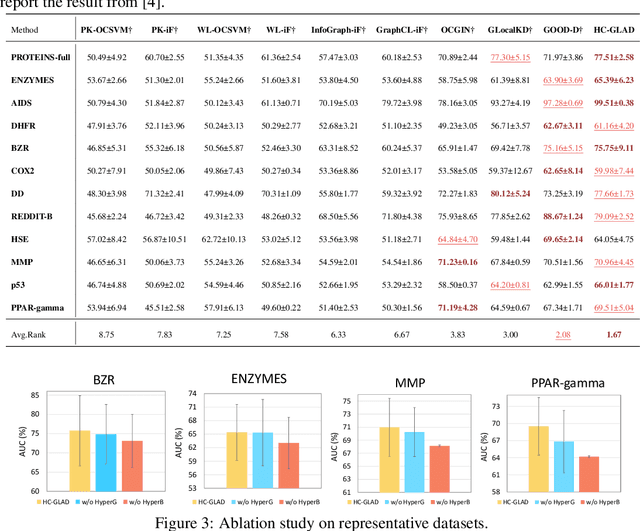
Unsupervised graph-level anomaly detection (UGAD) has garnered increasing attention in recent years due to its significance. However, most existing methods only rely on traditional graph neural networks to explore pairwise relationships but such kind of pairwise edges are not enough to describe multifaceted relationships involving anomaly. There is an emergency need to exploit node group information which plays a crucial role in UGAD. In addition, most previous works ignore the global underlying properties (e.g., hierarchy and power-law structure) which are common in real-world graph datasets and therefore are indispensable factors on UGAD task. In this paper, we propose a novel Dual Hyperbolic Contrastive Learning for Unsupervised Graph-Level Anomaly Detection (HC-GLAD in short). To exploit node group connections, we construct hypergraphs based on gold motifs and subsequently perform hypergraph convolution. Furthermore, to preserve the hierarchy of real-world graphs, we introduce hyperbolic geometry into this field and conduct both graph and hypergraph embedding learning in hyperbolic space with hyperboloid model. To the best of our knowledge, this is the first work to simultaneously apply hypergraph with node group connections and hyperbolic geometry into this field. Extensive experiments on several real world datasets of different fields demonstrate the superiority of HC-GLAD on UGAD task. The code is available at https://github.com/Yali-F/HC-GLAD.

Hypformer: Exploring Efficient Hyperbolic Transformer Fully in Hyperbolic Space

Hyperbolic geometry have shown significant potential in modeling complex structured data, particularly those with underlying tree-like and hierarchical structures. Despite the impressive performance of various hyperbolic neural networks across numerous domains, research on adapting the Transformer to hyperbolic space remains limited. Previous attempts have mainly focused on modifying self-attention modules in the Transformer. However, these efforts have fallen short of developing a complete hyperbolic Transformer. This stems primarily from: (i) the absence of well-defined modules in hyperbolic space, including linear transformation layers, LayerNorm layers, activation functions, dropout operations, etc. (ii) the quadratic time complexity of the existing hyperbolic self-attention module w.r.t the number of input tokens, which hinders its scalability. To address these challenges, we propose, Hypformer, a novel hyperbolic Transformer based on the Lorentz model of hyperbolic geometry. In Hypformer, we introduce two foundational blocks that define the essential modules of the Transformer in hyperbolic space. Furthermore, we develop a linear self-attention mechanism in hyperbolic space, enabling hyperbolic Transformer to process billion-scale graph data and long-sequence inputs for the first time. Our experimental results confirm the effectiveness and efficiency of Hypformer across various datasets, demonstrating its potential as an effective and scalable solution for large-scale data representation and large models.

HiHPQ: Hierarchical Hyperbolic Product Quantization for Unsupervised Image Retrieval

Existing unsupervised deep product quantization methods primarily aim for the increased similarity between different views of the identical image, whereas the delicate multi-level semantic similarities preserved between images are overlooked. Moreover, these methods predominantly focus on the Euclidean space for computational convenience, compromising their ability to map the multi-level semantic relationships between images effectively. To mitigate these shortcomings, we propose a novel unsupervised product quantization method dubbed \textbf{Hi}erarchical \textbf{H}yperbolic \textbf{P}roduct \textbf{Q}uantization (HiHPQ), which learns quantized representations by incorporating hierarchical semantic similarity within hyperbolic geometry. Specifically, we propose a hyperbolic product quantizer, where the hyperbolic codebook attention mechanism and the quantized contrastive learning on the hyperbolic product manifold are introduced to expedite quantization. Furthermore, we propose a hierarchical semantics learning module, designed to enhance the distinction between similar and non-matching images for a query by utilizing the extracted hierarchical semantics as an additional training supervision. Experiments on benchmarks show that our proposed method outperforms state-of-the-art baselines.

Alignment and Outer Shell Isotropy for Hyperbolic Graph Contrastive Learning

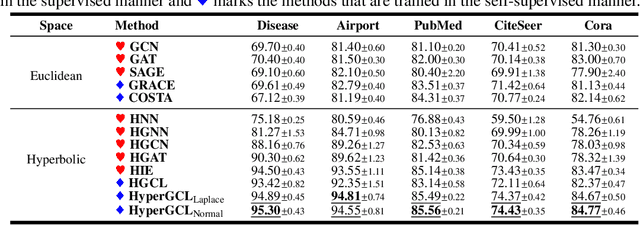
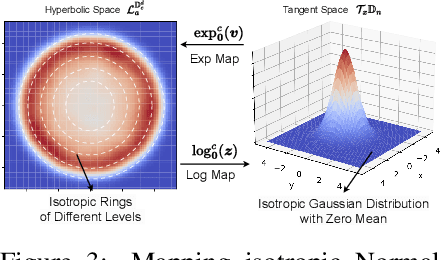
Learning good self-supervised graph representations that are beneficial to downstream tasks is challenging. Among a variety of methods, contrastive learning enjoys competitive performance. The embeddings of contrastive learning are arranged on a hypersphere that enables the Cosine distance measurement in the Euclidean space. However, the underlying structure of many domains such as graphs exhibits highly non-Euclidean latent geometry. To this end, we propose a novel contrastive learning framework to learn high-quality graph embedding. Specifically, we design the alignment metric that effectively captures the hierarchical data-invariant information, as well as we propose a substitute of uniformity metric to prevent the so-called dimensional collapse. We show that in the hyperbolic space one has to address the leaf- and height-level uniformity which are related to properties of trees, whereas in the ambient space of the hyperbolic manifold, these notions translate into imposing an isotropic ring density towards boundaries of Poincar\'e ball. This ring density can be easily imposed by promoting the isotropic feature distribution on the tangent space of manifold. In the experiments, we demonstrate the efficacy of our proposed method across different hyperbolic graph embedding techniques in both supervised and self-supervised learning settings.