Learning Along the Arrow of Time: Hyperbolic Geometry for Backward-Compatible Representation Learning

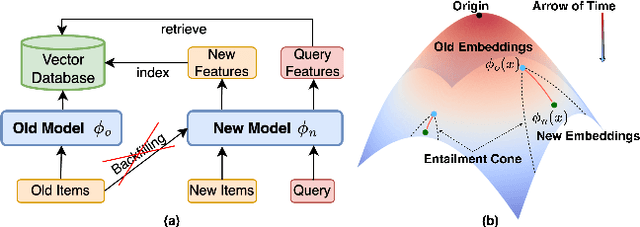
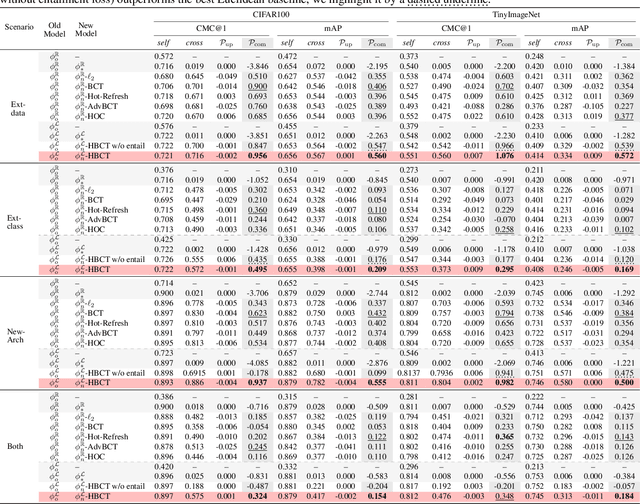
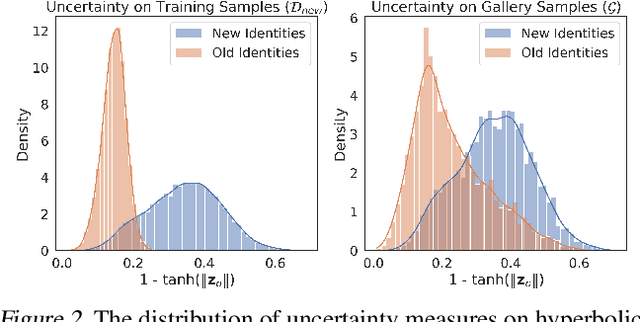
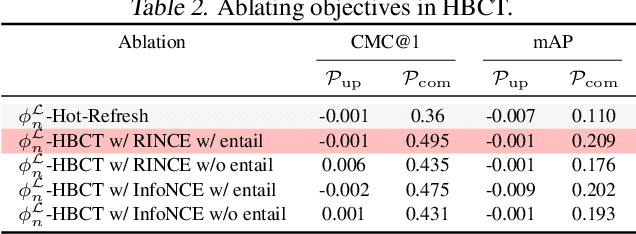
Backward compatible representation learning enables updated models to integrate seamlessly with existing ones, avoiding to reprocess stored data. Despite recent advances, existing compatibility approaches in Euclidean space neglect the uncertainty in the old embedding model and force the new model to reconstruct outdated representations regardless of their quality, thereby hindering the learning process of the new model. In this paper, we propose to switch perspectives to hyperbolic geometry, where we treat time as a natural axis for capturing a model's confidence and evolution. By lifting embeddings into hyperbolic space and constraining updated embeddings to lie within the entailment cone of the old ones, we maintain generational consistency across models while accounting for uncertainties in the representations. To further enhance compatibility, we introduce a robust contrastive alignment loss that dynamically adjusts alignment weights based on the uncertainty of the old embeddings. Experiments validate the superiority of the proposed method in achieving compatibility, paving the way for more resilient and adaptable machine learning systems.

HELM: Hyperbolic Large Language Models via Mixture-of-Curvature Experts

Large language models (LLMs) have shown great success in text modeling tasks across domains. However, natural language exhibits inherent semantic hierarchies and nuanced geometric structure, which current LLMs do not capture completely owing to their reliance on Euclidean operations. Recent studies have also shown that not respecting the geometry of token embeddings leads to training instabilities and degradation of generative capabilities. These findings suggest that shifting to non-Euclidean geometries can better align language models with the underlying geometry of text. We thus propose to operate fully in Hyperbolic space, known for its expansive, scale-free, and low-distortion properties. We thus introduce HELM, a family of HypErbolic Large Language Models, offering a geometric rethinking of the Transformer-based LLM that addresses the representational inflexibility, missing set of necessary operations, and poor scalability of existing hyperbolic LMs. We additionally introduce a Mixture-of-Curvature Experts model, HELM-MICE, where each expert operates in a distinct curvature space to encode more fine-grained geometric structure from text, as well as a dense model, HELM-D. For HELM-MICE, we further develop hyperbolic Multi-Head Latent Attention (HMLA) for efficient, reduced-KV-cache training and inference. For both models, we develop essential hyperbolic equivalents of rotary positional encodings and RMS normalization. We are the first to train fully hyperbolic LLMs at billion-parameter scale, and evaluate them on well-known benchmarks such as MMLU and ARC, spanning STEM problem-solving, general knowledge, and commonsense reasoning. Our results show consistent gains from our HELM architectures -- up to 4% -- over popular Euclidean architectures used in LLaMA and DeepSeek, highlighting the efficacy and enhanced reasoning afforded by hyperbolic geometry in large-scale LM pretraining.

Towards Non-Euclidean Foundation Models: Advancing AI Beyond Euclidean Frameworks

In the era of foundation models and Large Language Models (LLMs), Euclidean space is the de facto geometric setting of our machine learning architectures. However, recent literature has demonstrated that this choice comes with fundamental limitations. To that end, non-Euclidean learning is quickly gaining traction, particularly in web-related applications where complex relationships and structures are prevalent. Non-Euclidean spaces, such as hyperbolic, spherical, and mixed-curvature spaces, have been shown to provide more efficient and effective representations for data with intrinsic geometric properties, including web-related data like social network topology, query-document relationships, and user-item interactions. Integrating foundation models with non-Euclidean geometries has great potential to enhance their ability to capture and model the underlying structures, leading to better performance in search, recommendations, and content understanding. This workshop focuses on the intersection of Non-Euclidean Foundation Models and Geometric Learning (NEGEL), exploring its potential benefits, including the potential benefits for advancing web-related technologies, challenges, and future directions. Workshop page: [https://hyperboliclearning.github.io/events/www2025workshop](https://hyperboliclearning.github.io/events/www2025workshop)

HMamba: Hyperbolic Mamba for Sequential Recommendation

Sequential recommendation systems have become a cornerstone of personalized services, adept at modeling the temporal evolution of user preferences by capturing dynamic interaction sequences. Existing approaches predominantly rely on traditional models, including RNNs and Transformers. Despite their success in local pattern recognition, Transformer-based methods suffer from quadratic computational complexity and a tendency toward superficial attention patterns, limiting their ability to infer enduring preference hierarchies in sequential recommendation data. Recent advances in Mamba-based sequential models introduce linear-time efficiency but remain constrained by Euclidean geometry, failing to leverage the intrinsic hyperbolic structure of recommendation data. To bridge this gap, we propose Hyperbolic Mamba, a novel architecture that unifies the efficiency of Mamba's selective state space mechanism with hyperbolic geometry's hierarchical representational power. Our framework introduces (1) a hyperbolic selective state space that maintains curvature-aware sequence modeling and (2) stabilized Riemannian operations to enable scalable training. Experiments across four benchmarks demonstrate that Hyperbolic Mamba achieves 3-11% improvement while retaining Mamba's linear-time efficiency, enabling real-world deployment. This work establishes a new paradigm for efficient, hierarchy-aware sequential modeling.

CLIP-Powered Domain Generalization and Domain Adaptation: A Comprehensive Survey

As machine learning evolves, domain generalization (DG) and domain adaptation (DA) have become crucial for enhancing model robustness across diverse environments. Contrastive Language-Image Pretraining (CLIP) plays a significant role in these tasks, offering powerful zero-shot capabilities that allow models to perform effectively in unseen domains. However, there remains a significant gap in the literature, as no comprehensive survey currently exists that systematically explores the applications of CLIP in DG and DA, highlighting the necessity for this review. This survey presents a comprehensive review of CLIP's applications in DG and DA. In DG, we categorize methods into optimizing prompt learning for task alignment and leveraging CLIP as a backbone for effective feature extraction, both enhancing model adaptability. For DA, we examine both source-available methods utilizing labeled source data and source-free approaches primarily based on target domain data, emphasizing knowledge transfer mechanisms and strategies for improved performance across diverse contexts. Key challenges, including overfitting, domain diversity, and computational efficiency, are addressed, alongside future research opportunities to advance robustness and efficiency in practical applications. By synthesizing existing literature and pinpointing critical gaps, this survey provides valuable insights for researchers and practitioners, proposing directions for effectively leveraging CLIP to enhance methodologies in domain generalization and adaptation. Ultimately, this work aims to foster innovation and collaboration in the quest for more resilient machine learning models that can perform reliably across diverse real-world scenarios. A more up-to-date version of the papers is maintained at: https://github.com/jindongli-Ai/Survey_on_CLIP-Powered_Domain_Generalization_and_Adaptation.

Revisiting CLIP for SF-OSDA: Unleashing Zero-Shot Potential with Adaptive Threshold and Training-Free Feature Filtering

Source-Free Unsupervised Open-Set Domain Adaptation (SF-OSDA) methods using CLIP face significant issues: (1) while heavily dependent on domain-specific threshold selection, existing methods employ simple fixed thresholds, underutilizing CLIP's zero-shot potential in SF-OSDA scenarios; and (2) overlook intrinsic class tendencies while employing complex training to enforce feature separation, incurring deployment costs and feature shifts that compromise CLIP's generalization ability. To address these issues, we propose CLIPXpert, a novel SF-OSDA approach that integrates two key components: an adaptive thresholding strategy and an unknown class feature filtering module. Specifically, the Box-Cox GMM-Based Adaptive Thresholding (BGAT) module dynamically determines the optimal threshold by estimating sample score distributions, balancing known class recognition and unknown class sample detection. Additionally, the Singular Value Decomposition (SVD)-Based Unknown-Class Feature Filtering (SUFF) module reduces the tendency of unknown class samples towards known classes, improving the separation between known and unknown classes. Experiments show that our source-free and training-free method outperforms state-of-the-art trained approach UOTA by 1.92% on the DomainNet dataset, achieves SOTA-comparable performance on datasets such as Office-Home, and surpasses other SF-OSDA methods. This not only validates the effectiveness of our proposed method but also highlights CLIP's strong zero-shot potential for SF-OSDA tasks.

HyperCore: The Core Framework for Building Hyperbolic Foundation Models with Comprehensive Modules

Hyperbolic neural networks have emerged as a powerful tool for modeling hierarchical data across diverse modalities. Recent studies show that token distributions in foundation models exhibit scale-free properties, suggesting that hyperbolic space is a more suitable ambient space than Euclidean space for many pre-training and downstream tasks. However, existing tools lack essential components for building hyperbolic foundation models, making it difficult to leverage recent advancements. We introduce HyperCore, a comprehensive open-source framework that provides core modules for constructing hyperbolic foundation models across multiple modalities. HyperCore's modules can be effortlessly combined to develop novel hyperbolic foundation models, eliminating the need to extensively modify Euclidean modules from scratch and possible redundant research efforts. To demonstrate its versatility, we build and test the first fully hyperbolic vision transformers (LViT) with a fine-tuning pipeline, the first fully hyperbolic multimodal CLIP model (L-CLIP), and a hybrid Graph RAG with a hyperbolic graph encoder. Our experiments demonstrate that LViT outperforms its Euclidean counterpart. Additionally, we benchmark and reproduce experiments across hyperbolic GNNs, CNNs, Transformers, and vision Transformers to highlight HyperCore's advantages.

Position: Beyond Euclidean -- Foundation Models Should Embrace Non-Euclidean Geometries

In the era of foundation models and Large Language Models (LLMs), Euclidean space has been the de facto geometric setting for machine learning architectures. However, recent literature has demonstrated that this choice comes with fundamental limitations. At a large scale, real-world data often exhibit inherently non-Euclidean structures, such as multi-way relationships, hierarchies, symmetries, and non-isotropic scaling, in a variety of domains, such as languages, vision, and the natural sciences. It is challenging to effectively capture these structures within the constraints of Euclidean spaces. This position paper argues that moving beyond Euclidean geometry is not merely an optional enhancement but a necessity to maintain the scaling law for the next-generation of foundation models. By adopting these geometries, foundation models could more efficiently leverage the aforementioned structures. Task-aware adaptability that dynamically reconfigures embeddings to match the geometry of downstream applications could further enhance efficiency and expressivity. Our position is supported by a series of theoretical and empirical investigations of prevalent foundation models.Finally, we outline a roadmap for integrating non-Euclidean geometries into foundation models, including strategies for building geometric foundation models via fine-tuning, training from scratch, and hybrid approaches.

Hierarchical Graph Topic Modeling with Topic Tree-based Transformer

Textual documents are commonly connected in a hierarchical graph structure where a central document links to others with an exponentially growing connectivity. Though Hyperbolic Graph Neural Networks (HGNNs) excel at capturing such graph hierarchy, they cannot model the rich textual semantics within documents. Moreover, text contents in documents usually discuss topics of different specificity. Hierarchical Topic Models (HTMs) discover such latent topic hierarchy within text corpora. However, most of them focus on the textual content within documents, and ignore the graph adjacency across interlinked documents. We thus propose a Hierarchical Graph Topic Modeling Transformer to integrate both topic hierarchy within documents and graph hierarchy across documents into a unified Transformer. Specifically, to incorporate topic hierarchy within documents, we design a topic tree and infer a hierarchical tree embedding for hierarchical topic modeling. To preserve both topic and graph hierarchies, we design our model in hyperbolic space and propose Hyperbolic Doubly Recurrent Neural Network, which models ancestral and fraternal tree structure. Both hierarchies are inserted into each Transformer layer to learn unified representations. Both supervised and unsupervised experiments verify the effectiveness of our model.

A Survey of Personalized Large Language Models: Progress and Future Directions

Large Language Models (LLMs) excel in handling general knowledge tasks, yet they struggle with user-specific personalization, such as understanding individual emotions, writing styles, and preferences. Personalized Large Language Models (PLLMs) tackle these challenges by leveraging individual user data, such as user profiles, historical dialogues, content, and interactions, to deliver responses that are contextually relevant and tailored to each user's specific needs. This is a highly valuable research topic, as PLLMs can significantly enhance user satisfaction and have broad applications in conversational agents, recommendation systems, emotion recognition, medical assistants, and more. This survey reviews recent advancements in PLLMs from three technical perspectives: prompting for personalized context (input level), finetuning for personalized adapters (model level), and alignment for personalized preferences (objective level). To provide deeper insights, we also discuss current limitations and outline several promising directions for future research. Updated information about this survey can be found at the https://github.com/JiahongLiu21/Awesome-Personalized-Large-Language-Models.