Alignment and Outer Shell Isotropy for Hyperbolic Graph Contrastive Learning
Paper and Code
Oct 27, 2023

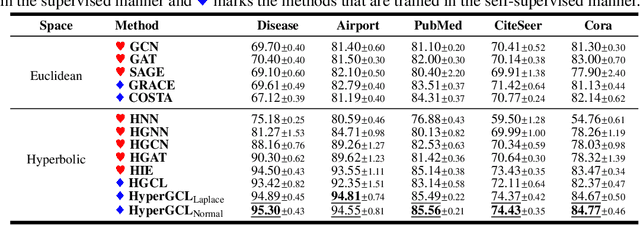
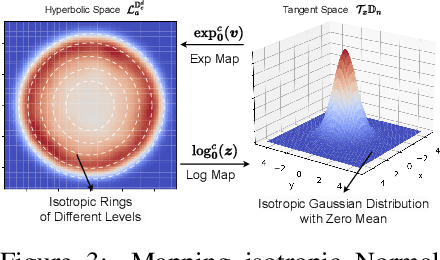
Learning good self-supervised graph representations that are beneficial to downstream tasks is challenging. Among a variety of methods, contrastive learning enjoys competitive performance. The embeddings of contrastive learning are arranged on a hypersphere that enables the Cosine distance measurement in the Euclidean space. However, the underlying structure of many domains such as graphs exhibits highly non-Euclidean latent geometry. To this end, we propose a novel contrastive learning framework to learn high-quality graph embedding. Specifically, we design the alignment metric that effectively captures the hierarchical data-invariant information, as well as we propose a substitute of uniformity metric to prevent the so-called dimensional collapse. We show that in the hyperbolic space one has to address the leaf- and height-level uniformity which are related to properties of trees, whereas in the ambient space of the hyperbolic manifold, these notions translate into imposing an isotropic ring density towards boundaries of Poincar\'e ball. This ring density can be easily imposed by promoting the isotropic feature distribution on the tangent space of manifold. In the experiments, we demonstrate the efficacy of our proposed method across different hyperbolic graph embedding techniques in both supervised and self-supervised learning settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge