GeoNorm: Unify Pre-Norm and Post-Norm with Geodesic Optimization

The placement of normalization layers, specifically Pre-Norm and Post-Norm, remains an open question in Transformer architecture design. In this work, we rethink these approaches through the lens of manifold optimization, interpreting the outputs of the Feed-Forward Network (FFN) and attention layers as update directions in optimization. Building on this perspective, we introduce GeoNorm, a novel method that replaces standard normalization with geodesic updates on the manifold. Furthermore, analogous to learning rate schedules, we propose a layer-wise update decay for the FFN and attention components. Comprehensive experiments demonstrate that GeoNorm consistently outperforms existing normalization methods in Transformer models. Crucially, GeoNorm can be seamlessly integrated into standard Transformer architectures, achieving performance improvements with negligible additional computational cost.

GenAR: Next-Scale Autoregressive Generation for Spatial Gene Expression Prediction

Spatial Transcriptomics (ST) offers spatially resolved gene expression but remains costly. Predicting expression directly from widely available Hematoxylin and Eosin (H&E) stained images presents a cost-effective alternative. However, most computational approaches (i) predict each gene independently, overlooking co-expression structure, and (ii) cast the task as continuous regression despite expression being discrete counts. This mismatch can yield biologically implausible outputs and complicate downstream analyses. We introduce GenAR, a multi-scale autoregressive framework that refines predictions from coarse to fine. GenAR clusters genes into hierarchical groups to expose cross-gene dependencies, models expression as codebook-free discrete token generation to directly predict raw counts, and conditions decoding on fused histological and spatial embeddings. From an information-theoretic perspective, the discrete formulation avoids log-induced biases and the coarse-to-fine factorization aligns with a principled conditional decomposition. Extensive experimental results on four Spatial Transcriptomics datasets across different tissue types demonstrate that GenAR achieves state-of-the-art performance, offering potential implications for precision medicine and cost-effective molecular profiling. Code is publicly available at https://github.com/oyjr/genar.

SAS: Simulated Attention Score

The attention mechanism is a core component of the Transformer architecture. Various methods have been developed to compute attention scores, including multi-head attention (MHA), multi-query attention, group-query attention and so on. We further analyze the MHA and observe that its performance improves as the number of attention heads increases, provided the hidden size per head remains sufficiently large. Therefore, increasing both the head count and hidden size per head with minimal parameter overhead can lead to significant performance gains at a low cost. Motivated by this insight, we introduce Simulated Attention Score (SAS), which maintains a compact model size while simulating a larger number of attention heads and hidden feature dimension per head. This is achieved by projecting a low-dimensional head representation into a higher-dimensional space, effectively increasing attention capacity without increasing parameter count. Beyond the head representations, we further extend the simulation approach to feature dimension of the key and query embeddings, enhancing expressiveness by mimicking the behavior of a larger model while preserving the original model size. To control the parameter cost, we also propose Parameter-Efficient Attention Aggregation (PEAA). Comprehensive experiments on a variety of datasets and tasks demonstrate the effectiveness of the proposed SAS method, achieving significant improvements over different attention variants.

Automatic Rank Determination for Low-Rank Adaptation via Submodular Function Maximization

In this paper, we propose SubLoRA, a rank determination method for Low-Rank Adaptation (LoRA) based on submodular function maximization. In contrast to prior approaches, such as AdaLoRA, that rely on first-order (linearized) approximations of the loss function, SubLoRA utilizes second-order information to capture the potentially complex loss landscape by incorporating the Hessian matrix. We show that the linearization becomes inaccurate and ill-conditioned when the LoRA parameters have been well optimized, motivating the need for a more reliable and nuanced second-order formulation. To this end, we reformulate the rank determination problem as a combinatorial optimization problem with a quadratic objective. However, solving this problem exactly is NP-hard in general. To overcome the computational challenge, we introduce a submodular function maximization framework and devise a greedy algorithm with approximation guarantees. We derive a sufficient and necessary condition under which the rank-determination objective becomes submodular, and construct a closed-form projection of the Hessian matrix that satisfies this condition while maintaining computational efficiency. Our method combines solid theoretical foundations, second-order accuracy, and practical computational efficiency. We further extend SubLoRA to a joint optimization setting, alternating between LoRA parameter updates and rank determination under a rank budget constraint. Extensive experiments on fine-tuning physics-informed neural networks (PINNs) for solving partial differential equations (PDEs) demonstrate the effectiveness of our approach. Results show that SubLoRA outperforms existing methods in both rank determination and joint training performance.

Self-Adjust Softmax

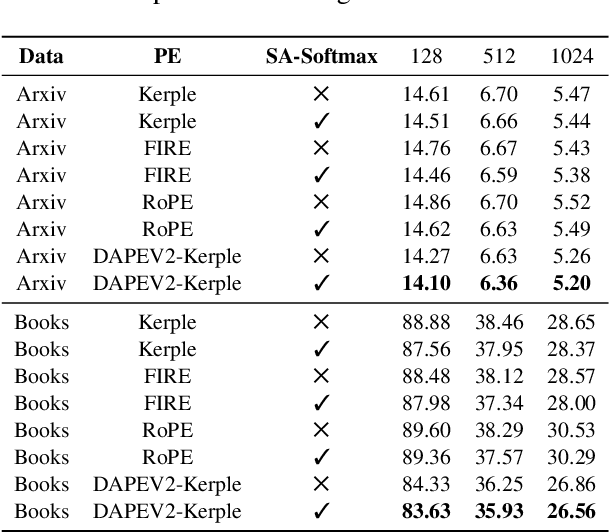
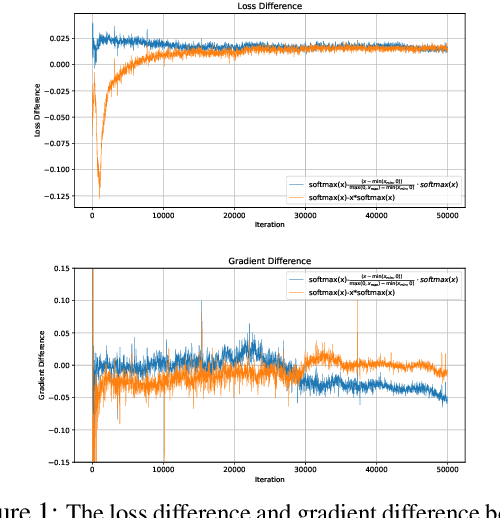
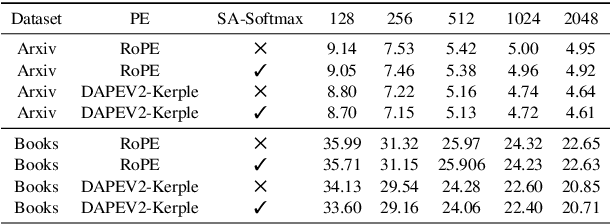
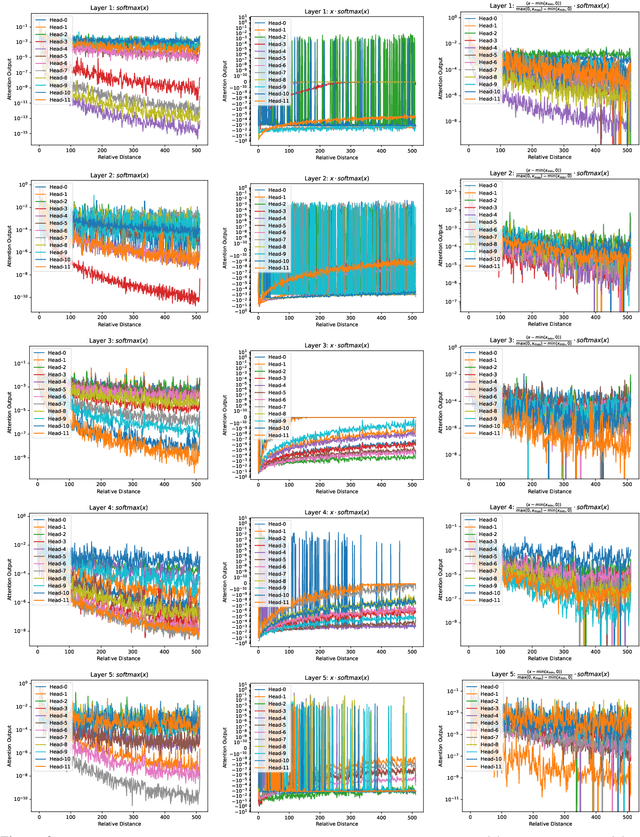
The softmax function is crucial in Transformer attention, which normalizes each row of the attention scores with summation to one, achieving superior performances over other alternative functions. However, the softmax function can face a gradient vanishing issue when some elements of the attention scores approach extreme values, such as probabilities close to one or zero. In this paper, we propose Self-Adjust Softmax (SA-Softmax) to address this issue by modifying $softmax(x)$ to $x \cdot softmax(x)$ and its normalized variant $\frac{(x - min(x_{\min},0))}{max(0,x_{max})-min(x_{min},0)} \cdot softmax(x)$. We theoretically show that SA-Softmax provides enhanced gradient properties compared to the vanilla softmax function. Moreover, SA-Softmax Attention can be seamlessly integrated into existing Transformer models to their attention mechanisms with minor adjustments. We conducted experiments to evaluate the empirical performance of Transformer models using SA-Softmax compared to the vanilla softmax function. These experiments, involving models with up to 2.7 billion parameters, are conducted across diverse datasets, language tasks, and positional encoding methods.

Low Tensor-Rank Adaptation of Kolmogorov--Arnold Networks

Kolmogorov--Arnold networks (KANs) have demonstrated their potential as an alternative to multi-layer perceptions (MLPs) in various domains, especially for science-related tasks. However, transfer learning of KANs remains a relatively unexplored area. In this paper, inspired by Tucker decomposition of tensors and evidence on the low tensor-rank structure in KAN parameter updates, we develop low tensor-rank adaptation (LoTRA) for fine-tuning KANs. We study the expressiveness of LoTRA based on Tucker decomposition approximations. Furthermore, we provide a theoretical analysis to select the learning rates for each LoTRA component to enable efficient training. Our analysis also shows that using identical learning rates across all components leads to inefficient training, highlighting the need for an adaptive learning rate strategy. Beyond theoretical insights, we explore the application of LoTRA for efficiently solving various partial differential equations (PDEs) by fine-tuning KANs. Additionally, we propose Slim KANs that incorporate the inherent low-tensor-rank properties of KAN parameter tensors to reduce model size while maintaining superior performance. Experimental results validate the efficacy of the proposed learning rate selection strategy and demonstrate the effectiveness of LoTRA for transfer learning of KANs in solving PDEs. Further evaluations on Slim KANs for function representation and image classification tasks highlight the expressiveness of LoTRA and the potential for parameter reduction through low tensor-rank decomposition.

SepLLM: Accelerate Large Language Models by Compressing One Segment into One Separator

Large Language Models (LLMs) have exhibited exceptional performance across a spectrum of natural language processing tasks. However, their substantial sizes pose considerable challenges, particularly in computational demands and inference speed, due to their quadratic complexity. In this work, we have identified a key pattern: certain seemingly meaningless special tokens (i.e., separators) contribute disproportionately to attention scores compared to semantically meaningful tokens. This observation suggests that information of the segments between these separator tokens can be effectively condensed into the separator tokens themselves without significant information loss. Guided by this insight, we introduce SepLLM, a plug-and-play framework that accelerates inference by compressing these segments and eliminating redundant tokens. Additionally, we implement efficient kernels for training acceleration. Experimental results across training-free, training-from-scratch, and post-training settings demonstrate SepLLM's effectiveness. Notably, using the Llama-3-8B backbone, SepLLM achieves over 50% reduction in KV cache on the GSM8K-CoT benchmark while maintaining comparable performance. Furthermore, in streaming settings, SepLLM effectively processes sequences of up to 4 million tokens or more while maintaining consistent language modeling capabilities.

DAPE V2: Process Attention Score as Feature Map for Length Extrapolation

The attention mechanism is a fundamental component of the Transformer model, contributing to interactions among distinct tokens, in contrast to earlier feed-forward neural networks. In general, the attention scores are determined simply by the key-query products. However, this work's occasional trial (combining DAPE and NoPE) of including additional MLPs on attention scores without position encoding indicates that the classical key-query multiplication may limit the performance of Transformers. In this work, we conceptualize attention as a feature map and apply the convolution operator (for neighboring attention scores across different heads) to mimic the processing methods in computer vision. Specifically, the main contribution of this paper is identifying and interpreting the Transformer length extrapolation problem as a result of the limited expressiveness of the naive query and key dot product, and we successfully translate the length extrapolation issue into a well-understood feature map processing problem. The novel insight, which can be adapted to various attention-related models, reveals that the current Transformer architecture has the potential for further evolution. Extensive experiments demonstrate that treating attention as a feature map and applying convolution as a processing method significantly enhances Transformer performance.

CAPE: Context-Adaptive Positional Encoding for Length Extrapolation

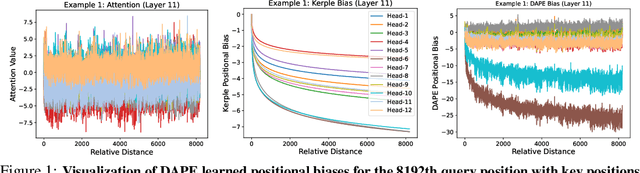
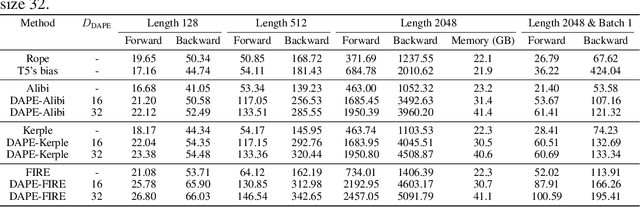
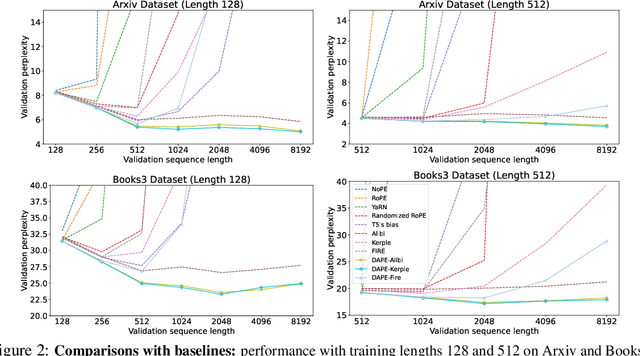
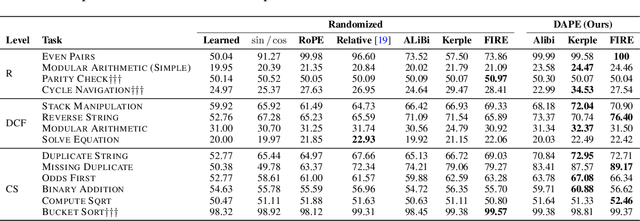
Positional encoding plays a crucial role in transformers, significantly impacting model performance and length generalization. Prior research has introduced absolute positional encoding (APE) and relative positional encoding (RPE) to distinguish token positions in given sequences. However, both APE and RPE remain fixed after model training regardless of input data, limiting their adaptability and flexibility. Hence, we expect that the desired positional encoding should be context-adaptive and can be dynamically adjusted with the given attention. In this paper, we propose a Context-Adaptive Positional Encoding (CAPE) method, which dynamically and semantically adjusts based on input context and learned fixed priors. Experimental validation on real-world datasets (Arxiv, Books3, and CHE) demonstrates that CAPE enhances model performances in terms of trained length and length generalization, where the improvements are statistically significant. The model visualization suggests that our model can keep both local and anti-local information. Finally, we successfully train the model on sequence length 128 and achieve better performance at evaluation sequence length 8192, compared with other static positional encoding methods, revealing the benefit of the adaptive positional encoding method.

On the Expressive Power of a Variant of the Looped Transformer

Besides natural language processing, transformers exhibit extraordinary performance in solving broader applications, including scientific computing and computer vision. Previous works try to explain this from the expressive power and capability perspectives that standard transformers are capable of performing some algorithms. To empower transformers with algorithmic capabilities and motivated by the recently proposed looped transformer (Yang et al., 2024; Giannou et al., 2023), we design a novel transformer block, dubbed Algorithm Transformer (abbreviated as AlgoFormer). Compared with the standard transformer and vanilla looped transformer, the proposed AlgoFormer can achieve significantly higher expressiveness in algorithm representation when using the same number of parameters. In particular, inspired by the structure of human-designed learning algorithms, our transformer block consists of a pre-transformer that is responsible for task pre-processing, a looped transformer for iterative optimization algorithms, and a post-transformer for producing the desired results after post-processing. We provide theoretical evidence of the expressive power of the AlgoFormer in solving some challenging problems, mirroring human-designed algorithms. Furthermore, some theoretical and empirical results are presented to show that the designed transformer has the potential to be smarter than human-designed algorithms. Experimental results demonstrate the empirical superiority of the proposed transformer in that it outperforms the standard transformer and vanilla looped transformer in some challenging tasks.