Large-scale Stochastic Optimization of NDCG Surrogates for Deep Learning with Provable Convergence
Paper and Code
Apr 06, 2022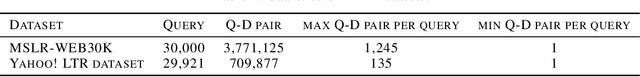

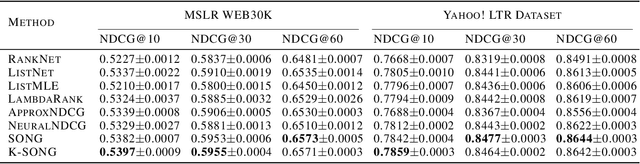

NDCG, namely Normalized Discounted Cumulative Gain, is a widely used ranking metric in information retrieval and machine learning. However, efficient and provable stochastic methods for maximizing NDCG are still lacking, especially for deep models. In this paper, we propose a principled approach to optimize NDCG and its top-$K$ variant. First, we formulate a novel compositional optimization problem for optimizing the NDCG surrogate, and a novel bilevel compositional optimization problem for optimizing the top-$K$ NDCG surrogate. Then, we develop efficient stochastic algorithms with provable convergence guarantees for the non-convex objectives. Different from existing NDCG optimization methods, the per-iteration complexity of our algorithms scales with the mini-batch size instead of the number of total items. To improve the effectiveness for deep learning, we further propose practical strategies by using initial warm-up and stop gradient operator. Experimental results on multiple datasets demonstrate that our methods outperform prior ranking approaches in terms of NDCG. To the best of our knowledge, this is the first time that stochastic algorithms are proposed to optimize NDCG with a provable convergence guarantee.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge