Blockwise Stochastic Variance-Reduced Methods with Parallel Speedup for Multi-Block Bilevel Optimization
Paper and Code
Jun 02, 2023
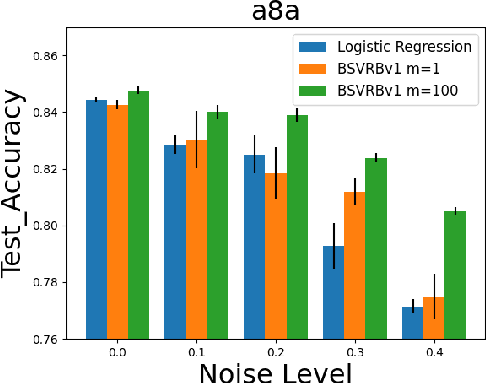
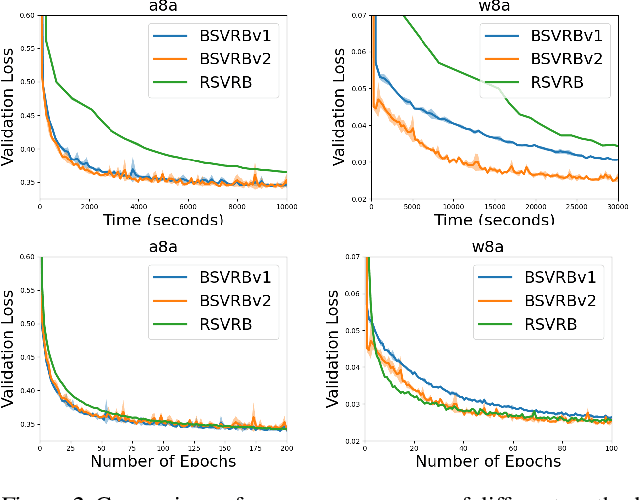
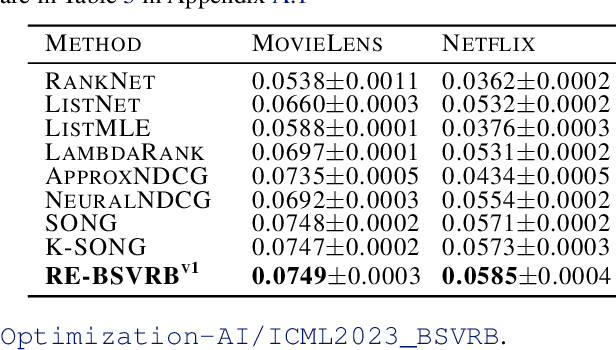
In this paper, we consider non-convex multi-block bilevel optimization (MBBO) problems, which involve $m\gg 1$ lower level problems and have important applications in machine learning. Designing a stochastic gradient and controlling its variance is more intricate due to the hierarchical sampling of blocks and data and the unique challenge of estimating hyper-gradient. We aim to achieve three nice properties for our algorithm: (a) matching the state-of-the-art complexity of standard BO problems with a single block; (b) achieving parallel speedup by sampling $I$ blocks and sampling $B$ samples for each sampled block per-iteration; (c) avoiding the computation of the inverse of a high-dimensional Hessian matrix estimator. However, it is non-trivial to achieve all of these by observing that existing works only achieve one or two of these properties. To address the involved challenges for achieving (a, b, c), we propose two stochastic algorithms by using advanced blockwise variance-reduction techniques for tracking the Hessian matrices (for low-dimensional problems) or the Hessian-vector products (for high-dimensional problems), and prove an iteration complexity of $O(\frac{m\epsilon^{-3}\mathbb{I}(I<m)}{I\sqrt{I}} + \frac{m\epsilon^{-3}}{I\sqrt{B}})$ for finding an $\epsilon$-stationary point under appropriate conditions. We also conduct experiments to verify the effectiveness of the proposed algorithms comparing with existing MBBO algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge