CLoVe: Encoding Compositional Language in Contrastive Vision-Language Models

Recent years have witnessed a significant increase in the performance of Vision and Language tasks. Foundational Vision-Language Models (VLMs), such as CLIP, have been leveraged in multiple settings and demonstrated remarkable performance across several tasks. Such models excel at object-centric recognition yet learn text representations that seem invariant to word order, failing to compose known concepts in novel ways. However, no evidence exists that any VLM, including large-scale single-stream models such as GPT-4V, identifies compositions successfully. In this paper, we introduce a framework to significantly improve the ability of existing models to encode compositional language, with over 10% absolute improvement on compositionality benchmarks, while maintaining or improving the performance on standard object-recognition and retrieval benchmarks. Our code and pre-trained models are publicly available at https://github.com/netflix/clove.

LibAUC: A Deep Learning Library for X-Risk Optimization

This paper introduces the award-winning deep learning (DL) library called LibAUC for implementing state-of-the-art algorithms towards optimizing a family of risk functions named X-risks. X-risks refer to a family of compositional functions in which the loss function of each data point is defined in a way that contrasts the data point with a large number of others. They have broad applications in AI for solving classical and emerging problems, including but not limited to classification for imbalanced data (CID), learning to rank (LTR), and contrastive learning of representations (CLR). The motivation of developing LibAUC is to address the convergence issues of existing libraries for solving these problems. In particular, existing libraries may not converge or require very large mini-batch sizes in order to attain good performance for these problems, due to the usage of the standard mini-batch technique in the empirical risk minimization (ERM) framework. Our library is for deep X-risk optimization (DXO) that has achieved great success in solving a variety of tasks for CID, LTR and CLR. The contributions of this paper include: (1) It introduces a new mini-batch based pipeline for implementing DXO algorithms, which differs from existing DL pipeline in the design of controlled data samplers and dynamic mini-batch losses; (2) It provides extensive benchmarking experiments for ablation studies and comparison with existing libraries. The LibAUC library features scalable performance for millions of items to be contrasted, faster and better convergence than existing libraries for optimizing X-risks, seamless PyTorch deployment and versatile APIs for various loss optimization. Our library is available to the open source community at https://github.com/Optimization-AI/LibAUC, to facilitate further academic research and industrial applications.

Not All Semantics are Created Equal: Contrastive Self-supervised Learning with Automatic Temperature Individualization

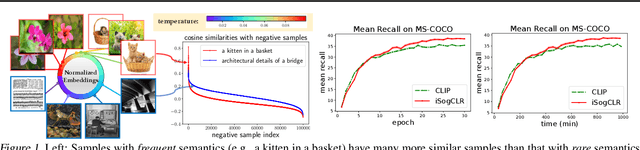
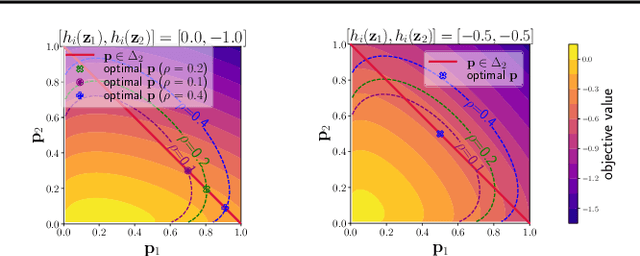
In this paper, we aim to optimize a contrastive loss with individualized temperatures in a principled and systematic manner for self-supervised learning. The common practice of using a global temperature parameter $\tau$ ignores the fact that ``not all semantics are created equal", meaning that different anchor data may have different numbers of samples with similar semantics, especially when data exhibits long-tails. First, we propose a new robust contrastive loss inspired by distributionally robust optimization (DRO), providing us an intuition about the effect of $\tau$ and a mechanism for automatic temperature individualization. Then, we propose an efficient stochastic algorithm for optimizing the robust contrastive loss with a provable convergence guarantee without using large mini-batch sizes. Theoretical and experimental results show that our algorithm automatically learns a suitable $\tau$ for each sample. Specifically, samples with frequent semantics use large temperatures to keep local semantic structures, while samples with rare semantics use small temperatures to induce more separable features. Our method not only outperforms prior strong baselines (e.g., SimCLR, CLIP) on unimodal and bimodal datasets with larger improvements on imbalanced data but also is less sensitive to hyper-parameters. To our best knowledge, this is the first methodical approach to optimizing a contrastive loss with individualized temperatures.

Provable Stochastic Optimization for Global Contrastive Learning: Small Batch Does Not Harm Performance

In this paper, we study contrastive learning from an optimization perspective, aiming to analyze and address a fundamental issue of existing contrastive learning methods that either rely on a large batch size or a large dictionary. We consider a global objective for contrastive learning, which contrasts each positive pair with all negative pairs for an anchor point. From the optimization perspective, we explain why existing methods such as SimCLR requires a large batch size in order to achieve a satisfactory result. In order to remove such requirement, we propose a memory-efficient Stochastic Optimization algorithm for solving the Global objective of Contrastive Learning of Representations, named SogCLR. We show that its optimization error is negligible under a reasonable condition after a sufficient number of iterations or is diminishing for a slightly different global contrastive objective. Empirically, we demonstrate that on ImageNet with a batch size 256, SogCLR achieves a performance of 69.4% for top-1 linear evaluation accuracy using ResNet-50, which is on par with SimCLR (69.3%) with a large batch size 8,192. We also attempt to show that the proposed optimization technique is generic and can be applied to solving other contrastive losses, e.g., two-way contrastive losses for bimodal contrastive learning.

Memory-based Optimization Methods for Model-Agnostic Meta-Learning

Recently, model-agnostic meta-learning (MAML) has garnered tremendous attention. However, stochastic optimization of MAML is still immature. Existing algorithms for MAML are based on the ``episode" idea by sampling a number of tasks and a number of data points for each sampled task at each iteration for updating the meta-model. However, they either do not necessarily guarantee convergence with a constant mini-batch size or require processing a larger number of tasks at every iteration, which is not viable for continual learning or cross-device federated learning where only a small number of tasks are available per-iteration or per-round. This paper addresses these issues by (i) proposing efficient memory-based stochastic algorithms for MAML with a diminishing convergence error, which only requires sampling a constant number of tasks and a constant number of examples per-task per-iteration; (ii) proposing communication-efficient distributed memory-based MAML algorithms for personalized federated learning in both the cross-device (w/ client sampling) and the cross-silo (w/o client sampling) settings. The key novelty of the proposed algorithms is to maintain an individual personalized model (aka memory) for each task besides the meta-model and only update them for the sampled tasks by a momentum method that incorporates historical updates at each iteration. The theoretical results significantly improve the optimization theory for MAML and the empirical results also corroborate the theory.

Federated Deep AUC Maximization for Heterogeneous Data with a Constant Communication Complexity

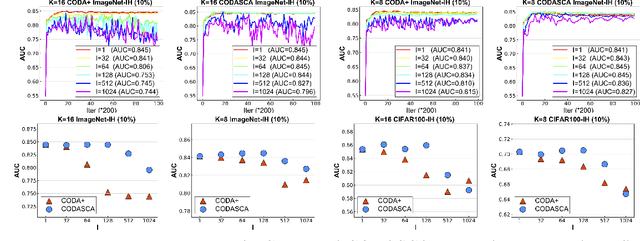
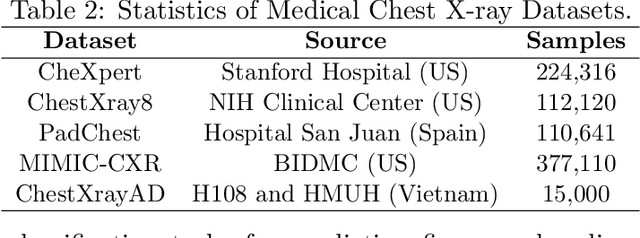
\underline{D}eep \underline{A}UC (area under the ROC curve) \underline{M}aximization (DAM) has attracted much attention recently due to its great potential for imbalanced data classification. However, the research on \underline{F}ederated \underline{D}eep \underline{A}UC \underline{M}aximization (FDAM) is still limited. Compared with standard federated learning (FL) approaches that focus on decomposable minimization objectives, FDAM is more complicated due to its minimization objective is non-decomposable over individual examples. In this paper, we propose improved FDAM algorithms for heterogeneous data by solving the popular non-convex strongly-concave min-max formulation of DAM in a distributed fashion. A striking result of this paper is that the communication complexity of the proposed algorithm is a constant independent of the number of machines and also independent of the accuracy level, which improves an existing result by orders of magnitude. Of independent interest, the proposed algorithm can also be applied to a class of non-convex-strongly-concave min-max problems. The experiments have demonstrated the effectiveness of our FDAM algorithm on benchmark datasets, and on medical chest X-ray images from different organizations. Our experiment shows that the performance of FDAM using data from multiple hospitals can improve the AUC score on testing data from a single hospital for detecting life-threatening diseases based on chest radiographs.

Robust Deep AUC Maximization: A New Surrogate Loss and Empirical Studies on Medical Image Classification

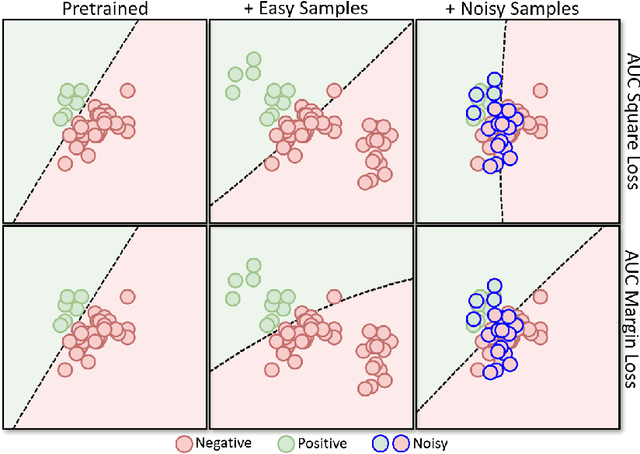
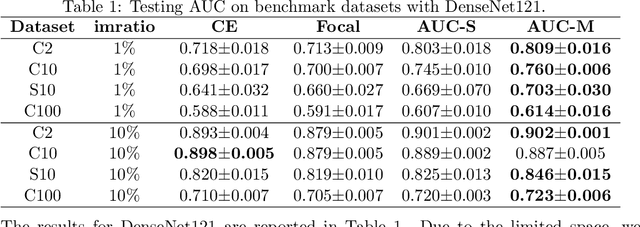
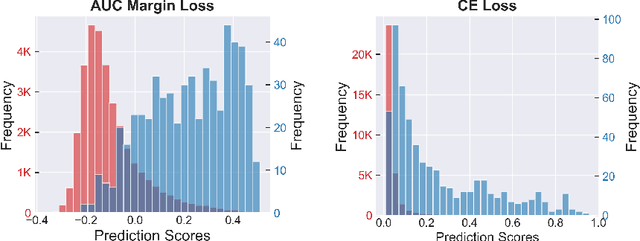
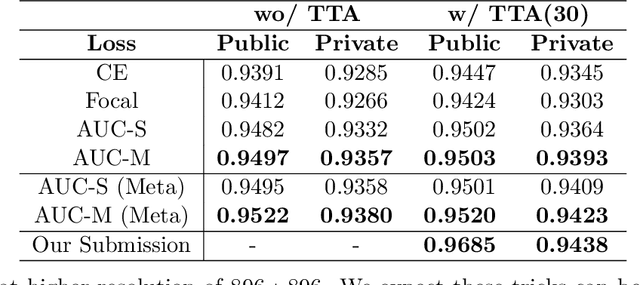
Deep AUC Maximization (DAM) is a paradigm for learning a deep neural network by maximizing the AUC score of the model on a dataset. Most previous works of AUC maximization focus on the perspective of optimization by designing efficient stochastic algorithms, and studies on generalization performance of DAM on difficult tasks are missing. In this work, we aim to make DAM more practical for interesting real-world applications (e.g., medical image classification). First, we propose a new margin-based surrogate loss function for the AUC score (named as the AUC margin loss). It is more robust than the commonly used AUC square loss, while enjoying the same advantage in terms of large-scale stochastic optimization. Second, we conduct empirical studies of our DAM method on difficult medical image classification tasks, namely classification of chest x-ray images for identifying many threatening diseases and classification of images of skin lesions for identifying melanoma. Our DAM method has achieved great success on these difficult tasks, i.e., the 1st place on Stanford CheXpert competition (by the paper submission date) and Top 1% rank (rank 33 out of 3314 teams) on Kaggle 2020 Melanoma classification competition. We also conduct extensive ablation studies to demonstrate the advantages of the new AUC margin loss over the AUC square loss on benchmark datasets. To the best of our knowledge, this is the first work that makes DAM succeed on large-scale medical image datasets.

Fast Objective and Duality Gap Convergence for Non-convex Strongly-concave Min-max Problems

This paper focuses on stochastic methods for solving smooth non-convex strongly-concave min-max problems, which have received increasing attention due to their potential applications in deep learning (e.g., deep AUC maximization). However, most of the existing algorithms are slow in practice, and their analysis revolves around the convergence to a nearly stationary point. We consider leveraging the Polyak-\L ojasiewicz (PL) condition to design faster stochastic algorithms with stronger convergence guarantee. Although PL condition has been utilized for designing many stochastic minimization algorithms, their applications for non-convex min-max optimization remains rare. In this paper, we propose and analyze proximal epoch-based methods, and establish fast convergence in terms of both {\bf the primal objective gap and the duality gap}. Our analysis is interesting in threefold: (i) it is based on a novel Lyapunov function that consists of the primal objective gap and the duality gap of a regularized function; (ii) it only requires a weaker PL condition for establishing the primal objective convergence than that required for the duality gap convergence; (iii) it yields the optimal dependence on the accuracy level $\epsilon$, i.e., $O(1/\epsilon)$. We also make explicit the dependence on the problem parameters and explore regions of weak convexity parameter that lead to improved dependence on condition numbers. Experiments on deep AUC maximization demonstrate the effectiveness of our methods. Our method also beats the 1st place on {\bf Stanford CheXpert competition} in terms of AUC on the public validation set.

Communication-Efficient Distributed Stochastic AUC Maximization with Deep Neural Networks

In this paper, we study distributed algorithms for large-scale AUC maximization with a deep neural network as a predictive model. Although distributed learning techniques have been investigated extensively in deep learning, they are not directly applicable to stochastic AUC maximization with deep neural networks due to its striking differences from standard loss minimization problems (e.g., cross-entropy). Towards addressing this challenge, we propose and analyze a communication-efficient distributed optimization algorithm based on a {\it non-convex concave} reformulation of the AUC maximization, in which the communication of both the primal variable and the dual variable between each worker and the parameter server only occurs after multiple steps of gradient-based updates in each worker. Compared with the naive parallel version of an existing algorithm that computes stochastic gradients at individual machines and averages them for updating the model parameter, our algorithm requires a much less number of communication rounds and still achieves a linear speedup in theory. To the best of our knowledge, this is the \textbf{first} work that solves the {\it non-convex concave min-max} problem for AUC maximization with deep neural networks in a communication-efficient distributed manner while still maintaining the linear speedup property in theory. Our experiments on several benchmark datasets show the effectiveness of our algorithm and also confirm our theory.

Stochastic AUC Maximization with Deep Neural Networks

Stochastic AUC maximization has garnered an increasing interest due to better fit to imbalanced data classification. However, existing works are limited to stochastic AUC maximization with a linear predictive model, which restricts its predictive power when dealing with extremely complex data. In this paper, we consider stochastic AUC maximization problem with a deep neural network as the predictive model. Building on the saddle point reformulation of a surrogated loss of AUC, the problem can be cast into a {\it non-convex concave} min-max problem. The main contribution made in this paper is to make stochastic AUC maximization more practical for deep neural networks and big data with theoretical insights as well. In particular, we propose to explore Polyak-\L{}ojasiewicz (PL) condition that has been proved and observed in deep learning, which enables us to develop new stochastic algorithms with even faster convergence rate and more practical step size scheme. An AdaGrad-style algorithm is also analyzed under the PL condition with adaptive convergence rate. Our experimental results demonstrate the effectiveness of the proposed algorithms.