Federated Deep AUC Maximization for Heterogeneous Data with a Constant Communication Complexity

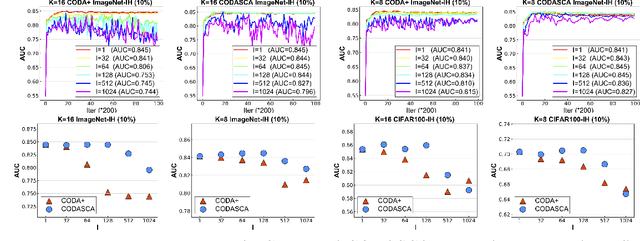
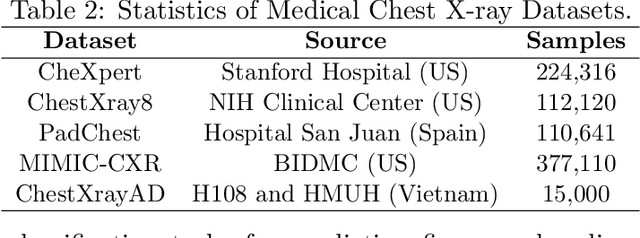
\underline{D}eep \underline{A}UC (area under the ROC curve) \underline{M}aximization (DAM) has attracted much attention recently due to its great potential for imbalanced data classification. However, the research on \underline{F}ederated \underline{D}eep \underline{A}UC \underline{M}aximization (FDAM) is still limited. Compared with standard federated learning (FL) approaches that focus on decomposable minimization objectives, FDAM is more complicated due to its minimization objective is non-decomposable over individual examples. In this paper, we propose improved FDAM algorithms for heterogeneous data by solving the popular non-convex strongly-concave min-max formulation of DAM in a distributed fashion. A striking result of this paper is that the communication complexity of the proposed algorithm is a constant independent of the number of machines and also independent of the accuracy level, which improves an existing result by orders of magnitude. Of independent interest, the proposed algorithm can also be applied to a class of non-convex-strongly-concave min-max problems. The experiments have demonstrated the effectiveness of our FDAM algorithm on benchmark datasets, and on medical chest X-ray images from different organizations. Our experiment shows that the performance of FDAM using data from multiple hospitals can improve the AUC score on testing data from a single hospital for detecting life-threatening diseases based on chest radiographs.