Function Aligned Regression: A Method Explicitly Learns Functional Derivatives from Data

Regression is a fundamental task in machine learning that has garnered extensive attention over the past decades. The conventional approach for regression involves employing loss functions that primarily concentrate on aligning model prediction with the ground truth for each individual data sample, which, as we show, can result in sub-optimal prediction of the relationships between the different samples. Recent research endeavors have introduced novel perspectives by incorporating label similarity information to regression. However, a notable gap persists in these approaches when it comes to fully capturing the intricacies of the underlying ground truth function. In this work, we propose FAR (Function Aligned Regression) as a arguably better and more efficient solution to fit the underlying function of ground truth by capturing functional derivatives. We demonstrate the effectiveness of the proposed method practically on 2 synthetic datasets and on 8 extensive real-world tasks from 6 benchmark datasets with other 8 competitive baselines. The code is open-sourced at \url{https://github.com/DixianZhu/FAR}.

Non-Smooth Weakly-Convex Finite-sum Coupled Compositional Optimization

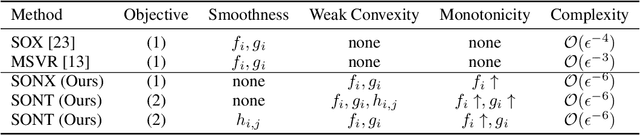
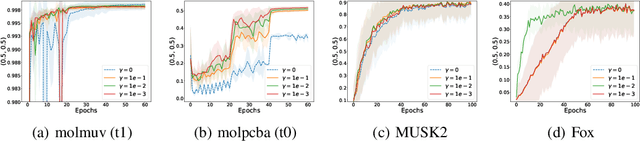
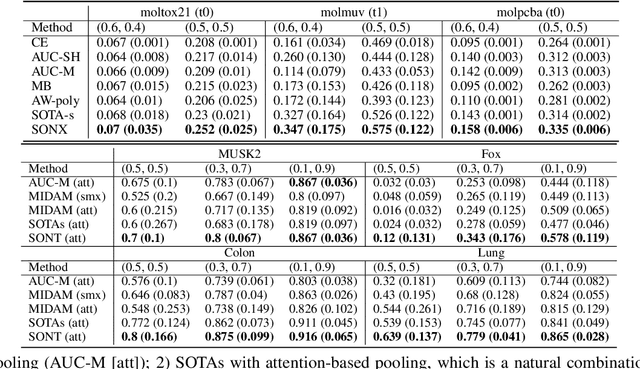
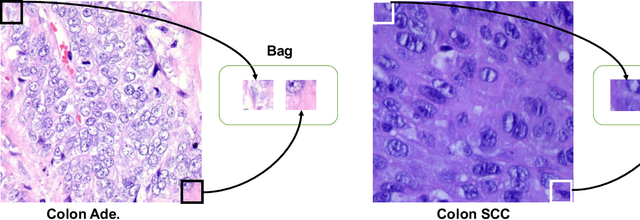
This paper investigates new families of compositional optimization problems, called $\underline{\bf n}$on-$\underline{\bf s}$mooth $\underline{\bf w}$eakly-$\underline{\bf c}$onvex $\underline{\bf f}$inite-sum $\underline{\bf c}$oupled $\underline{\bf c}$ompositional $\underline{\bf o}$ptimization (NSWC FCCO). There has been a growing interest in FCCO due to its wide-ranging applications in machine learning and AI, as well as its ability to address the shortcomings of stochastic algorithms based on empirical risk minimization. However, current research on FCCO presumes that both the inner and outer functions are smooth, limiting their potential to tackle a more diverse set of problems. Our research expands on this area by examining non-smooth weakly-convex FCCO, where the outer function is weakly convex and non-decreasing, and the inner function is weakly-convex. We analyze a single-loop algorithm and establish its complexity for finding an $\epsilon$-stationary point of the Moreau envelop of the objective function. Additionally, we also extend the algorithm to solving novel non-smooth weakly-convex tri-level finite-sum coupled compositional optimization problems, which feature a nested arrangement of three functions. Lastly, we explore the applications of our algorithms in deep learning for two-way partial AUC maximization and multi-instance two-way partial AUC maximization, using empirical studies to showcase the effectiveness of the proposed algorithms.

LibAUC: A Deep Learning Library for X-Risk Optimization

This paper introduces the award-winning deep learning (DL) library called LibAUC for implementing state-of-the-art algorithms towards optimizing a family of risk functions named X-risks. X-risks refer to a family of compositional functions in which the loss function of each data point is defined in a way that contrasts the data point with a large number of others. They have broad applications in AI for solving classical and emerging problems, including but not limited to classification for imbalanced data (CID), learning to rank (LTR), and contrastive learning of representations (CLR). The motivation of developing LibAUC is to address the convergence issues of existing libraries for solving these problems. In particular, existing libraries may not converge or require very large mini-batch sizes in order to attain good performance for these problems, due to the usage of the standard mini-batch technique in the empirical risk minimization (ERM) framework. Our library is for deep X-risk optimization (DXO) that has achieved great success in solving a variety of tasks for CID, LTR and CLR. The contributions of this paper include: (1) It introduces a new mini-batch based pipeline for implementing DXO algorithms, which differs from existing DL pipeline in the design of controlled data samplers and dynamic mini-batch losses; (2) It provides extensive benchmarking experiments for ablation studies and comparison with existing libraries. The LibAUC library features scalable performance for millions of items to be contrasted, faster and better convergence than existing libraries for optimizing X-risks, seamless PyTorch deployment and versatile APIs for various loss optimization. Our library is available to the open source community at https://github.com/Optimization-AI/LibAUC, to facilitate further academic research and industrial applications.

Provable Multi-instance Deep AUC Maximization with Stochastic Pooling

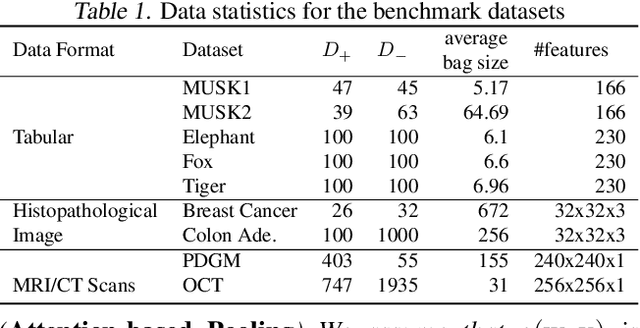
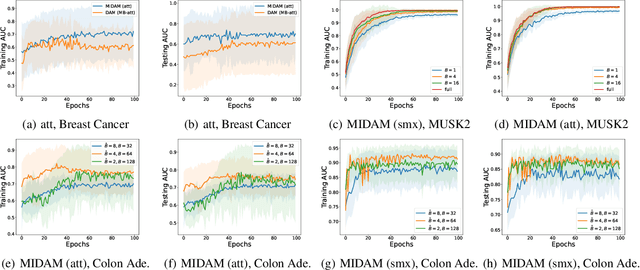
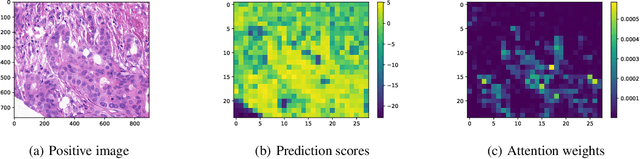
This paper considers a novel application of deep AUC maximization (DAM) for multi-instance learning (MIL), in which a single class label is assigned to a bag of instances (e.g., multiple 2D slices of a CT scan for a patient). We address a neglected yet non-negligible computational challenge of MIL in the context of DAM, i.e., bag size is too large to be loaded into {GPU} memory for backpropagation, which is required by the standard pooling methods of MIL. To tackle this challenge, we propose variance-reduced stochastic pooling methods in the spirit of stochastic optimization by formulating the loss function over the pooled prediction as a multi-level compositional function. By synthesizing techniques from stochastic compositional optimization and non-convex min-max optimization, we propose a unified and provable muli-instance DAM (MIDAM) algorithm with stochastic smoothed-max pooling or stochastic attention-based pooling, which only samples a few instances for each bag to compute a stochastic gradient estimator and to update the model parameter. We establish a similar convergence rate of the proposed MIDAM algorithm as the state-of-the-art DAM algorithms. Our extensive experiments on conventional MIL datasets and medical datasets demonstrate the superiority of our MIDAM algorithm.

Benchmarking Deep AUROC Optimization: Loss Functions and Algorithmic Choices

The area under the ROC curve (AUROC) has been vigorously applied for imbalanced classification and moreover combined with deep learning techniques. However, there is no existing work that provides sound information for peers to choose appropriate deep AUROC maximization techniques. In this work, we fill this gap from three aspects. (i) We benchmark a variety of loss functions with different algorithmic choices for deep AUROC optimization problem. We study the loss functions in two categories: pairwise loss and composite loss, which includes a total of 10 loss functions. Interestingly, we find composite loss, as an innovative loss function class, shows more competitive performance than pairwise loss from both training convergence and testing generalization perspectives. Nevertheless, data with more corrupted labels favors a pairwise symmetric loss. (ii) Moreover, we benchmark and highlight the essential algorithmic choices such as positive sampling rate, regularization, normalization/activation, and optimizers. Key findings include: higher positive sampling rate is likely to be beneficial for deep AUROC maximization; different datasets favors different weights of regularizations; appropriate normalization techniques, such as sigmoid and $\ell_2$ score normalization, could improve model performance. (iii) For optimization aspect, we benchmark SGD-type, Momentum-type, and Adam-type optimizers for both pairwise and composite loss. Our findings show that although Adam-type method is more competitive from training perspective, but it does not outperform others from testing perspective.

When AUC meets DRO: Optimizing Partial AUC for Deep Learning with Non-Convex Convergence Guarantee

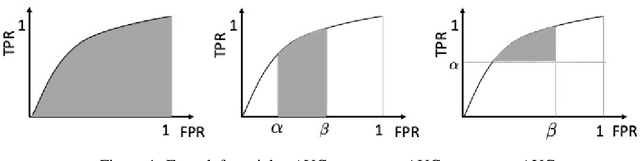
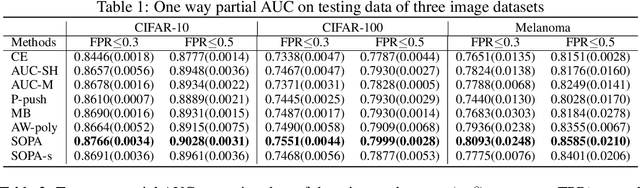
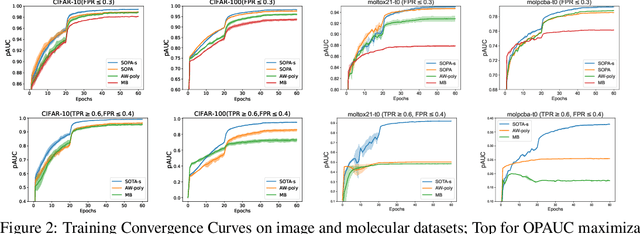
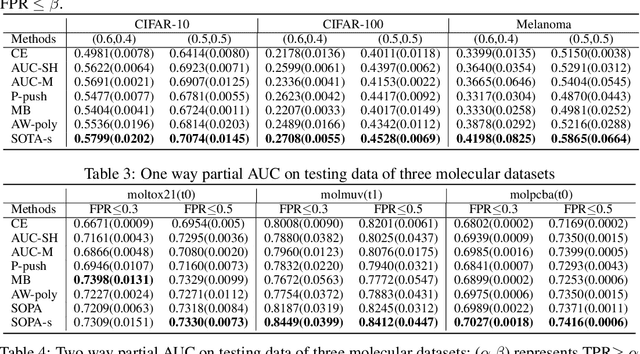
In this paper, we propose systematic and efficient gradient-based methods for both one-way and two-way partial AUC (pAUC) maximization that are applicable to deep learning. We propose new formulations of pAUC surrogate objectives by using the distributionally robust optimization (DRO) to define the loss for each individual positive data. We consider two formulations of DRO, one of which is based on conditional-value-at-risk (CVaR) that yields a non-smooth but exact estimator for pAUC, and another one is based on a KL divergence regularized DRO that yields an inexact but smooth (soft) estimator for pAUC. For both one-way and two-way pAUC maximization, we propose two algorithms and prove their convergence for optimizing their two formulations, respectively. Experiments demonstrate the effectiveness of the proposed algorithms for pAUC maximization for deep learning on various datasets.

A Unified DRO View of Multi-class Loss Functions with top-N Consistency

Multi-class classification is one of the most common tasks in machine learning applications, where data is labeled by one of many class labels. Many loss functions have been proposed for multi-class classification including two well-known ones, namely the cross-entropy (CE) loss and the crammer-singer (CS) loss (aka. the SVM loss). While CS loss has been used widely for traditional machine learning tasks, CE loss is usually a default choice for multi-class deep learning tasks. There are also top-$k$ variants of CS loss and CE loss that are proposed to promote the learning of a classifier for achieving better top-$k$ accuracy. Nevertheless, it still remains unclear the relationship between these different losses, which hinders our understanding of their expectations in different scenarios. In this paper, we present a unified view of the CS/CE losses and their smoothed top-$k$ variants by proposing a new family of loss functions, which are arguably better than the CS/CE losses when the given label information is incomplete and noisy. The new family of smooth loss functions named {label-distributionally robust (LDR) loss} is defined by leveraging the distributionally robust optimization (DRO) framework to model the uncertainty in the given label information, where the uncertainty over true class labels is captured by using distributional weights for each label regularized by a function.