FedPAE: Peer-Adaptive Ensemble Learning for Asynchronous and Model-Heterogeneous Federated Learning

Federated learning (FL) enables multiple clients with distributed data sources to collaboratively train a shared model without compromising data privacy. However, existing FL paradigms face challenges due to heterogeneity in client data distributions and system capabilities. Personalized federated learning (pFL) has been proposed to mitigate these problems, but often requires a shared model architecture and a central entity for parameter aggregation, resulting in scalability and communication issues. More recently, model-heterogeneous FL has gained attention due to its ability to support diverse client models, but existing methods are limited by their dependence on a centralized framework, synchronized training, and publicly available datasets. To address these limitations, we introduce Federated Peer-Adaptive Ensemble Learning (FedPAE), a fully decentralized pFL algorithm that supports model heterogeneity and asynchronous learning. Our approach utilizes a peer-to-peer model sharing mechanism and ensemble selection to achieve a more refined balance between local and global information. Experimental results show that FedPAE outperforms existing state-of-the-art pFL algorithms, effectively managing diverse client capabilities and demonstrating robustness against statistical heterogeneity.

Model Developmental Safety: A Safety-Centric Method and Applications in Vision-Language Models

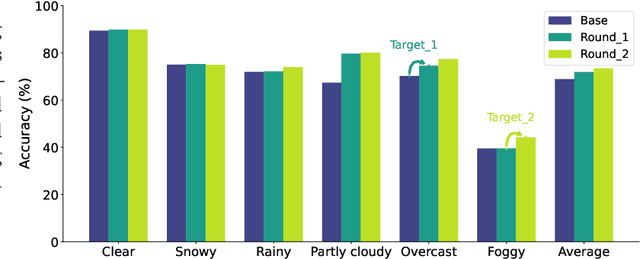
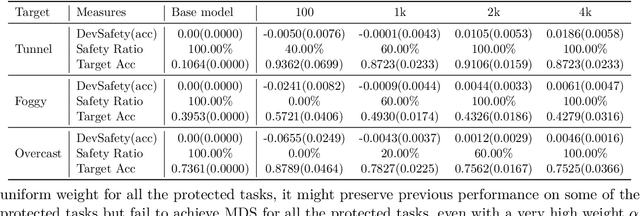
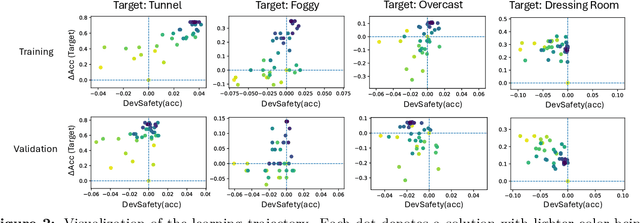
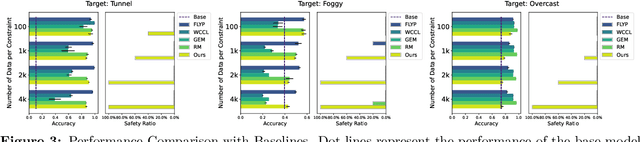
In the real world, a learning-enabled system usually undergoes multiple cycles of model development to enhance the system's ability to handle difficult or emerging tasks. This continual model development process raises a significant issue that the model development for acquiring new or improving existing capabilities may inadvertently lose capabilities of the old model, also known as catastrophic forgetting. Existing continual learning studies focus on mitigating catastrophic forgetting by trading off performance on previous tasks and new tasks to ensure good average performance. However, they are inadequate for many applications especially in safety-critical domains, as failure to strictly preserve the performance of the old model not only introduces safety risks and uncertainties but also imposes substantial expenses in the re-improving and re-validation of existing properties. To address this issue, we introduce model developmental safety as a guarantee of a learning system such that in the model development process the new model should strictly preserve the existing protected capabilities of the old model while improving its performance on target tasks. To ensure the model developmental safety, we present a safety-centric framework by formulating the model developmental safety as data-dependent constraints. Under this framework, we study how to develop a pretrained vision-language model (aka the CLIP model) for acquiring new capabilities or improving existing capabilities of image classification. We propose an efficient constrained optimization algorithm with theoretical guarantee and use its insights to finetune a CLIP model with task-dependent heads for promoting the model developmental safety. Our experiments on improving vision perception capabilities on autonomous driving and scene recognition datasets demonstrate the efficacy of the proposed approach.

Multi-Output Distributional Fairness via Post-Processing

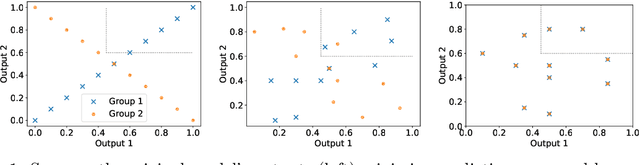
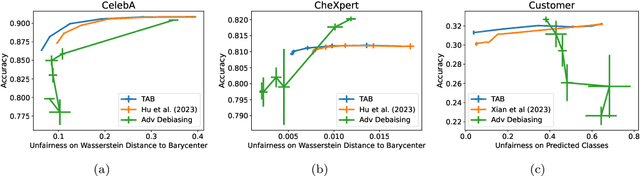
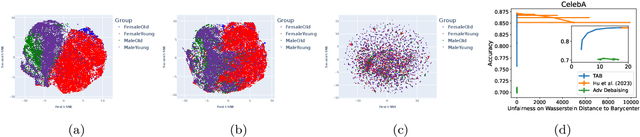
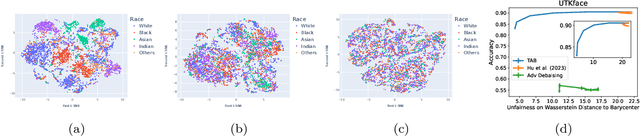
The post-processing approaches are becoming prominent techniques to enhance machine learning models' fairness because of their intuitiveness, low computational cost, and excellent scalability. However, most existing post-processing methods are designed for task-specific fairness measures and are limited to single-output models. In this paper, we introduce a post-processing method for multi-output models, such as the ones used for multi-task/multi-class classification and representation learning, to enhance a model's distributional parity, a task-agnostic fairness measure. Existing techniques to achieve distributional parity are based on the (inverse) cumulative density function of a model's output, which is limited to single-output models. Extending previous works, our method employs an optimal transport mapping to move a model's outputs across different groups towards their empirical Wasserstein barycenter. An approximation technique is applied to reduce the complexity of computing the exact barycenter and a kernel regression method is proposed for extending this process to out-of-sample data. Our empirical studies, which compare our method to current existing post-processing baselines on multi-task/multi-class classification and representation learning tasks, demonstrate the effectiveness of the proposed approach.

Provable Optimization for Adversarial Fair Self-supervised Contrastive Learning

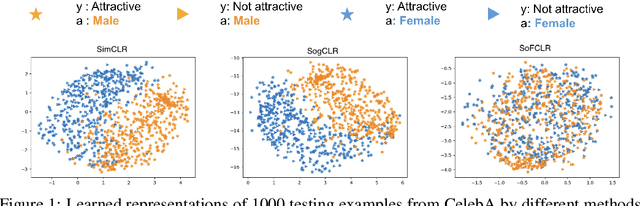
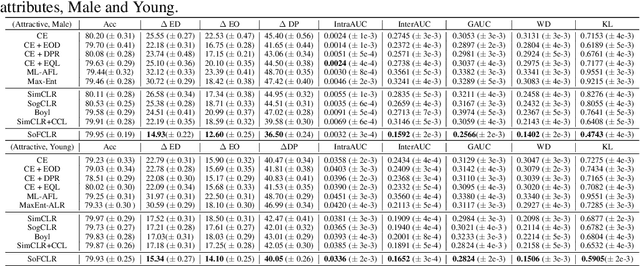
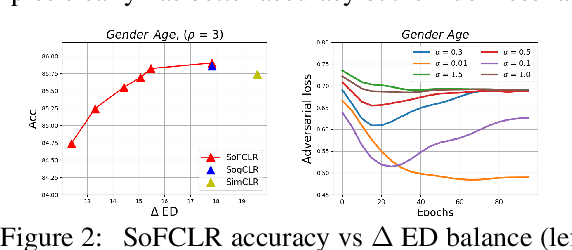
This paper studies learning fair encoders in a self-supervised learning (SSL) setting, in which all data are unlabeled and only a small portion of them are annotated with sensitive attribute. Adversarial fair representation learning is well suited for this scenario by minimizing a contrastive loss over unlabeled data while maximizing an adversarial loss of predicting the sensitive attribute over the data with sensitive attribute. Nevertheless, optimizing adversarial fair representation learning presents significant challenges due to solving a non-convex non-concave minimax game. The complexity deepens when incorporating a global contrastive loss that contrasts each anchor data point against all other examples. A central question is ``{\it can we design a provable yet efficient algorithm for solving adversarial fair self-supervised contrastive learning}?'' Building on advanced optimization techniques, we propose a stochastic algorithm dubbed SoFCLR with a convergence analysis under reasonable conditions without requring a large batch size. We conduct extensive experiments to demonstrate the effectiveness of the proposed approach for downstream classification with eight fairness notions.

First-order Methods for Affinely Constrained Composite Non-convex Non-smooth Problems: Lower Complexity Bound and Near-optimal Methods

Many recent studies on first-order methods (FOMs) focus on \emph{composite non-convex non-smooth} optimization with linear and/or nonlinear function constraints. Upper (or worst-case) complexity bounds have been established for these methods. However, little can be claimed about their optimality as no lower bound is known, except for a few special \emph{smooth non-convex} cases. In this paper, we make the first attempt to establish lower complexity bounds of FOMs for solving a class of composite non-convex non-smooth optimization with linear constraints. Assuming two different first-order oracles, we establish lower complexity bounds of FOMs to produce a (near) $\epsilon$-stationary point of a problem (and its reformulation) in the considered problem class, for any given tolerance $\epsilon>0$. In addition, we present an inexact proximal gradient (IPG) method by using the more relaxed one of the two assumed first-order oracles. The oracle complexity of the proposed IPG, to find a (near) $\epsilon$-stationary point of the considered problem and its reformulation, matches our established lower bounds up to a logarithmic factor. Therefore, our lower complexity bounds and the proposed IPG method are almost non-improvable.

Single-Loop Switching Subgradient Methods for Non-Smooth Weakly Convex Optimization with Non-Smooth Convex Constraints

In this paper, we consider a general non-convex constrained optimization problem, where the objective function is weakly convex and the constraint function is convex while they can both be non-smooth. This class of problems arises from many applications in machine learning such as fairness-aware supervised learning. To solve this problem, we consider the classical switching subgradient method by Polyak (1965), which is an intuitive and easily implementable first-order method. Before this work, its iteration complexity was only known for convex optimization. We prove its oracle complexity for finding a nearly stationary point when the objective function is non-convex. The analysis is derived separately when the constraint function is deterministic and stochastic. Compared to existing methods, especially the double-loop methods, the switching gradient method can be applied to non-smooth problems and only has a single loop, which saves the effort on tuning the number of inner iterations.

Stochastic Methods for AUC Optimization subject to AUC-based Fairness Constraints

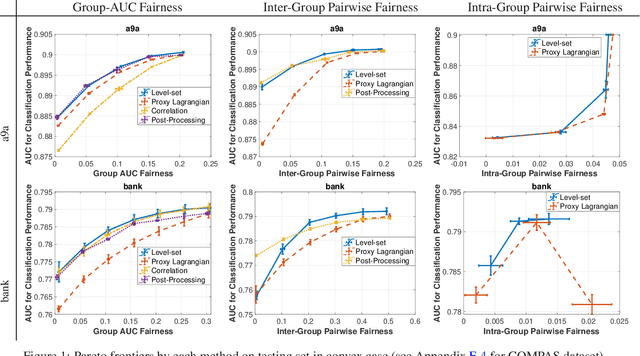
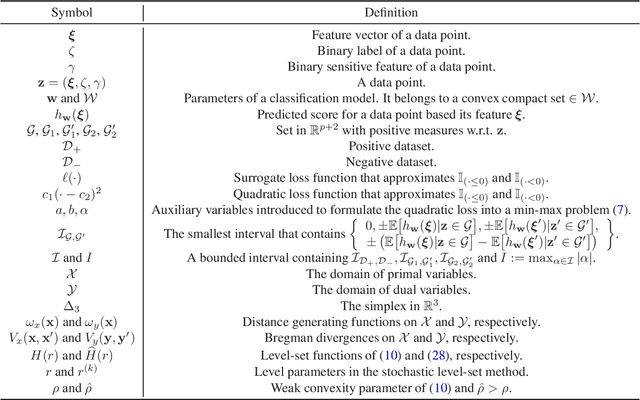
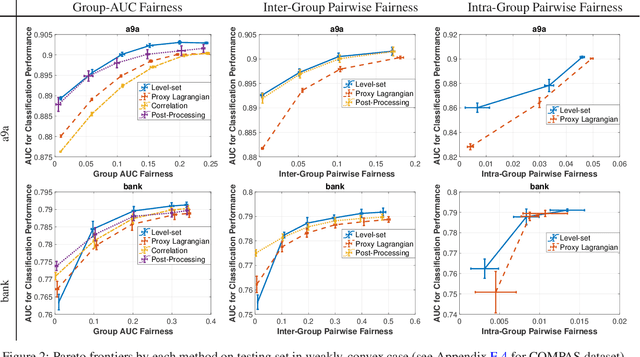
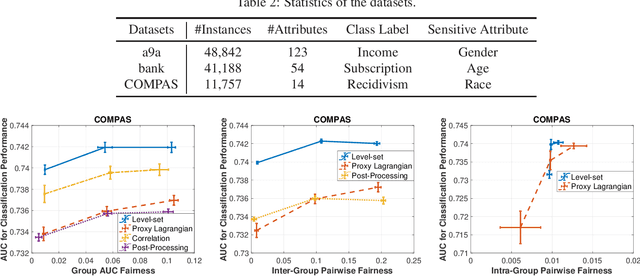
As machine learning being used increasingly in making high-stakes decisions, an arising challenge is to avoid unfair AI systems that lead to discriminatory decisions for protected population. A direct approach for obtaining a fair predictive model is to train the model through optimizing its prediction performance subject to fairness constraints, which achieves Pareto efficiency when trading off performance against fairness. Among various fairness metrics, the ones based on the area under the ROC curve (AUC) are emerging recently because they are threshold-agnostic and effective for unbalanced data. In this work, we formulate the training problem of a fairness-aware machine learning model as an AUC optimization problem subject to a class of AUC-based fairness constraints. This problem can be reformulated as a min-max optimization problem with min-max constraints, which we solve by stochastic first-order methods based on a new Bregman divergence designed for the special structure of the problem. We numerically demonstrate the effectiveness of our approach on real-world data under different fairness metrics.

ProtoX: Explaining a Reinforcement Learning Agent via Prototyping

While deep reinforcement learning has proven to be successful in solving control tasks, the "black-box" nature of an agent has received increasing concerns. We propose a prototype-based post-hoc policy explainer, ProtoX, that explains a blackbox agent by prototyping the agent's behaviors into scenarios, each represented by a prototypical state. When learning prototypes, ProtoX considers both visual similarity and scenario similarity. The latter is unique to the reinforcement learning context, since it explains why the same action is taken in visually different states. To teach ProtoX about visual similarity, we pre-train an encoder using contrastive learning via self-supervised learning to recognize states as similar if they occur close together in time and receive the same action from the black-box agent. We then add an isometry layer to allow ProtoX to adapt scenario similarity to the downstream task. ProtoX is trained via imitation learning using behavior cloning, and thus requires no access to the environment or agent. In addition to explanation fidelity, we design different prototype shaping terms in the objective function to encourage better interpretability. We conduct various experiments to test ProtoX. Results show that ProtoX achieved high fidelity to the original black-box agent while providing meaningful and understandable explanations.

Federated Learning on Adaptively Weighted Nodes by Bilevel Optimization

We propose a federated learning method with weighted nodes in which the weights can be modified to optimize the model's performance on a separate validation set. The problem is formulated as a bilevel optimization where the inner problem is a federated learning problem with weighted nodes and the outer problem focuses on optimizing the weights based on the validation performance of the model returned from the inner problem. A communication-efficient federated optimization algorithm is designed to solve this bilevel optimization problem. Under an error-bound assumption, we analyze the generalization performance of the output model and identify scenarios when our method is in theory superior to training a model only locally and to federated learning with static and evenly distributed weights.

Large-scale Optimization of Partial AUC in a Range of False Positive Rates

The area under the ROC curve (AUC) is one of the most widely used performance measures for classification models in machine learning. However, it summarizes the true positive rates (TPRs) over all false positive rates (FPRs) in the ROC space, which may include the FPRs with no practical relevance in some applications. The partial AUC, as a generalization of the AUC, summarizes only the TPRs over a specific range of the FPRs and is thus a more suitable performance measure in many real-world situations. Although partial AUC optimization in a range of FPRs had been studied, existing algorithms are not scalable to big data and not applicable to deep learning. To address this challenge, we cast the problem into a non-smooth difference-of-convex (DC) program for any smooth predictive functions (e.g., deep neural networks), which allowed us to develop an efficient approximated gradient descent method based on the Moreau envelope smoothing technique, inspired by recent advances in non-smooth DC optimization. To increase the efficiency of large data processing, we used an efficient stochastic block coordinate update in our algorithm. Our proposed algorithm can also be used to minimize the sum of ranked range loss, which also lacks efficient solvers. We established a complexity of $\tilde O(1/\epsilon^6)$ for finding a nearly $\epsilon$-critical solution. Finally, we numerically demonstrated the effectiveness of our proposed algorithms for both partial AUC maximization and sum of ranked range loss minimization.