Biased Dueling Bandits with Stochastic Delayed Feedback
Paper and Code
Aug 26, 2024
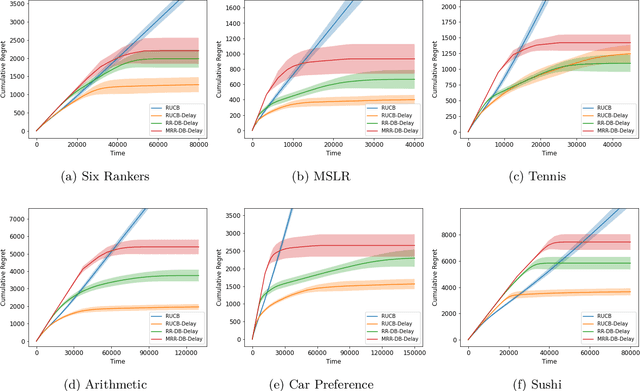
The dueling bandit problem, an essential variation of the traditional multi-armed bandit problem, has become significantly prominent recently due to its broad applications in online advertising, recommendation systems, information retrieval, and more. However, in many real-world applications, the feedback for actions is often subject to unavoidable delays and is not immediately available to the agent. This partially observable issue poses a significant challenge to existing dueling bandit literature, as it significantly affects how quickly and accurately the agent can update their policy on the fly. In this paper, we introduce and examine the biased dueling bandit problem with stochastic delayed feedback, revealing that this new practical problem will delve into a more realistic and intriguing scenario involving a preference bias between the selections. We present two algorithms designed to handle situations involving delay. Our first algorithm, requiring complete delay distribution information, achieves the optimal regret bound for the dueling bandit problem when there is no delay. The second algorithm is tailored for situations where the distribution is unknown, but only the expected value of delay is available. We provide a comprehensive regret analysis for the two proposed algorithms and then evaluate their empirical performance on both synthetic and real datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge