Unknown sparsity in compressed sensing: Denoising and inference
Paper and Code
Aug 31, 2017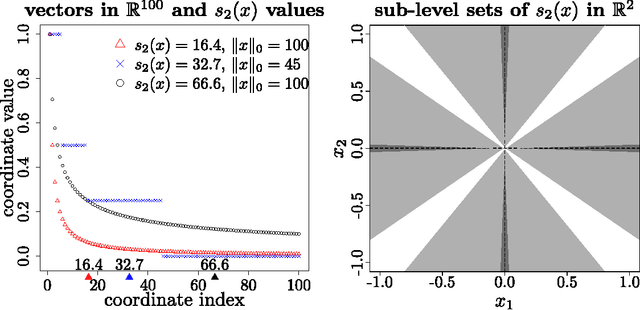
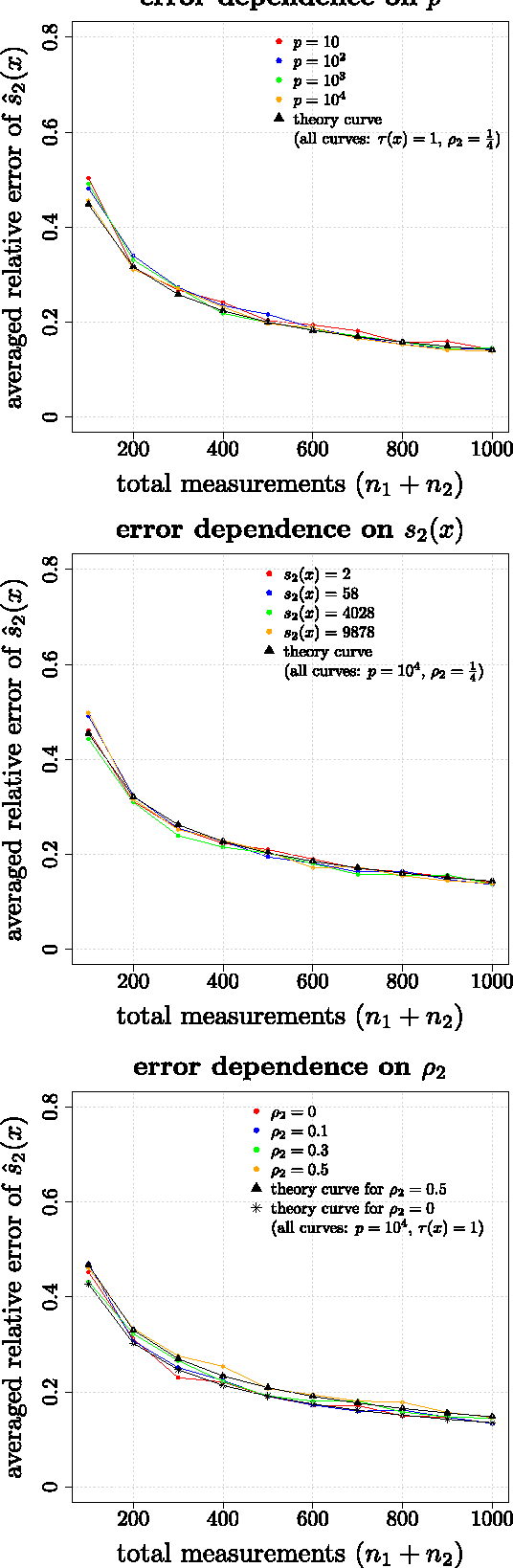

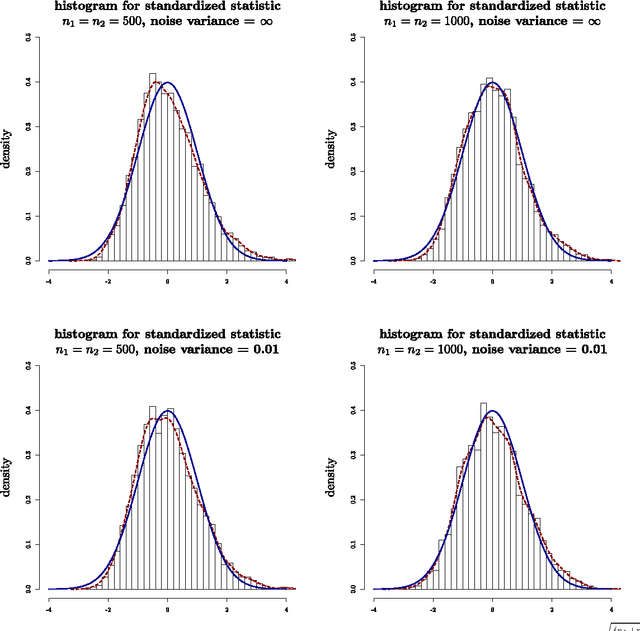
The theory of Compressed Sensing (CS) asserts that an unknown signal $x\in\mathbb{R}^p$ can be accurately recovered from an underdetermined set of $n$ linear measurements with $n\ll p$, provided that $x$ is sufficiently sparse. However, in applications, the degree of sparsity $\|x\|_0$ is typically unknown, and the problem of directly estimating $\|x\|_0$ has been a longstanding gap between theory and practice. A closely related issue is that $\|x\|_0$ is a highly idealized measure of sparsity, and for real signals with entries not equal to 0, the value $\|x\|_0=p$ is not a useful description of compressibility. In our previous conference paper [Lop13] that examined these problems, we considered an alternative measure of "soft" sparsity, $\|x\|_1^2/\|x\|_2^2$, and designed a procedure to estimate $\|x\|_1^2/\|x\|_2^2$ that does not rely on sparsity assumptions. The present work offers a new deconvolution-based method for estimating unknown sparsity, which has wider applicability and sharper theoretical guarantees. In particular, we introduce a family of entropy-based sparsity measures $s_q(x):=\big(\frac{\|x\|_q}{\|x\|_1}\big)^{\frac{q}{1-q}}$ parameterized by $q\in[0,\infty]$. This family interpolates between $\|x\|_0=s_0(x)$ and $\|x\|_1^2/\|x\|_2^2=s_2(x)$ as $q$ ranges over $[0,2]$. For any $q\in (0,2]\setminus\{1\}$, we propose an estimator $\hat{s}_q(x)$ whose relative error converges at the dimension-free rate of $1/\sqrt{n}$, even when $p/n\to\infty$. Our main results also describe the limiting distribution of $\hat{s}_q(x)$, as well as some connections to Basis Pursuit Denosing, the Lasso, deterministic measurement matrices, and inference problems in CS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge