Near-Optimal Distributed Linear-Quadratic Regulator for Networked Systems

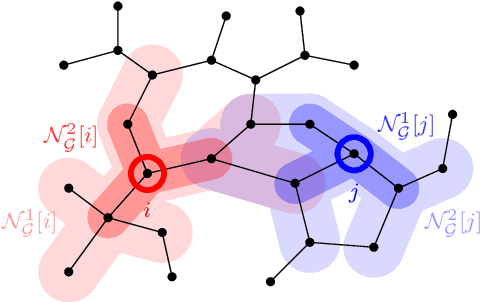
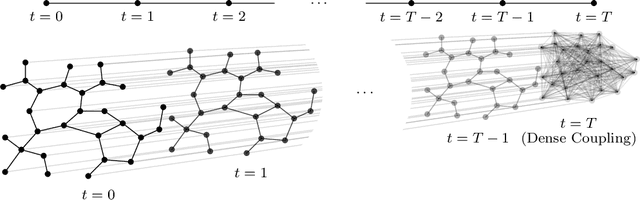
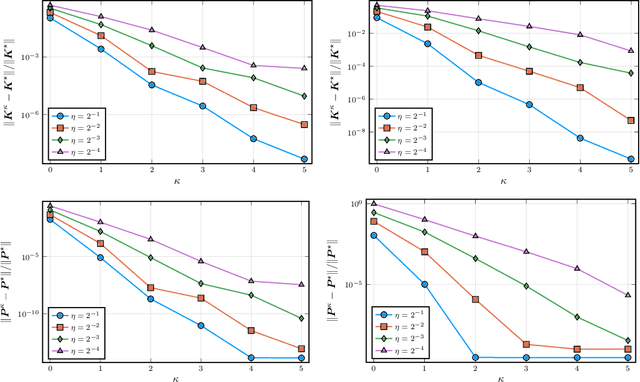
This paper studies the trade-off between the degree of decentralization and the performance of a distributed controller in a linear-quadratic control setting. We study a system of interconnected agents over a graph and a distributed controller, called $\kappa$-distributed control, which lets the agents make control decisions based on the state information within distance $\kappa$ on the underlying graph. This controller can tune its degree of decentralization using the parameter $\kappa$ and thus allows a characterization of the relationship between decentralization and performance. We show that under mild assumptions, including stabilizability, detectability, and a polynomially growing graph condition, the performance difference between $\kappa$-distributed control and centralized optimal control becomes exponentially small in $\kappa$. This result reveals that distributed control can achieve near-optimal performance with a moderate degree of decentralization, and thus it is an effective controller architecture for large-scale networked systems.