Weakly-Constrained 4D Var for Downscaling with Uncertainty using Data-Driven Surrogate Models

Dynamic downscaling typically involves using numerical weather prediction (NWP) solvers to refine coarse data to higher spatial resolutions. Data-driven models such as FourCastNet have emerged as a promising alternative to the traditional NWP models for forecasting. Once these models are trained, they are capable of delivering forecasts in a few seconds, thousands of times faster compared to classical NWP models. However, as the lead times, and, therefore, their forecast window, increase, these models show instability in that they tend to diverge from reality. In this paper, we propose to use data assimilation approaches to stabilize them when used for downscaling tasks. Data assimilation uses information from three different sources, namely an imperfect computational model based on partial differential equations (PDE), from noisy observations, and from an uncertainty-reflecting prior. In this work, when carrying out dynamic downscaling, we replace the computationally expensive PDE-based NWP models with FourCastNet in a ``weak-constrained 4DVar framework" that accounts for the implied model errors. We demonstrate the efficacy of this approach for a hurricane-tracking problem; moreover, the 4DVar framework naturally allows the expression and quantification of uncertainty. We demonstrate, using ERA5 data, that our approach performs better than the ensemble Kalman filter (EnKF) and the unstabilized FourCastNet model, both in terms of forecast accuracy and forecast uncertainty.

Learning the Evolution of Correlated Stochastic Power System Dynamics

A machine learning technique is proposed for quantifying uncertainty in power system dynamics with spatiotemporally correlated stochastic forcing. We learn one-dimensional linear partial differential equations for the probability density functions of real-valued quantities of interest. The method is suitable for high-dimensional systems and helps to alleviate the curse of dimensionality.

Using recurrent neural networks for nonlinear component computation in advection-dominated reduced-order models

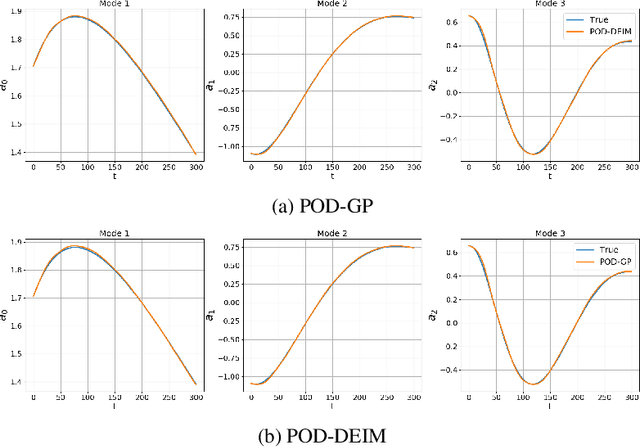
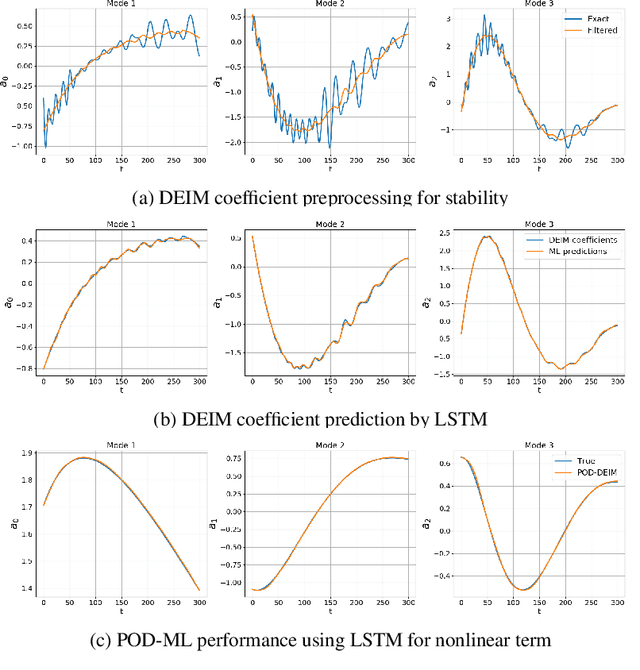
Rapid simulations of advection-dominated problems are vital for multiple engineering and geophysical applications. In this paper, we present a long short-term memory neural network to approximate the nonlinear component of the reduced-order model (ROM) of an advection-dominated partial differential equation. This is motivated by the fact that the nonlinear term is the most expensive component of a successful ROM. For our approach, we utilize a Galerkin projection to isolate the linear and the transient components of the dynamical system and then use discrete empirical interpolation to generate training data for supervised learning. We note that the numerical time-advancement and linear-term computation of the system ensure a greater preservation of physics than does a process that is fully modeled. Our results show that the proposed framework recovers transient dynamics accurately without nonlinear term computations in full-order space and represents a cost-effective alternative to solely equation-based ROMs.