Using recurrent neural networks for nonlinear component computation in advection-dominated reduced-order models
Paper and Code
Nov 01, 2019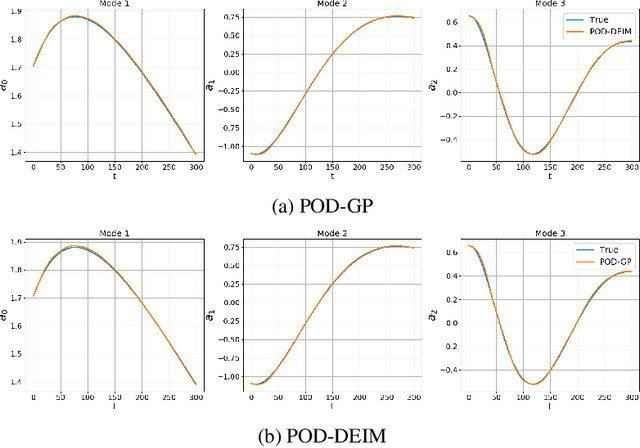
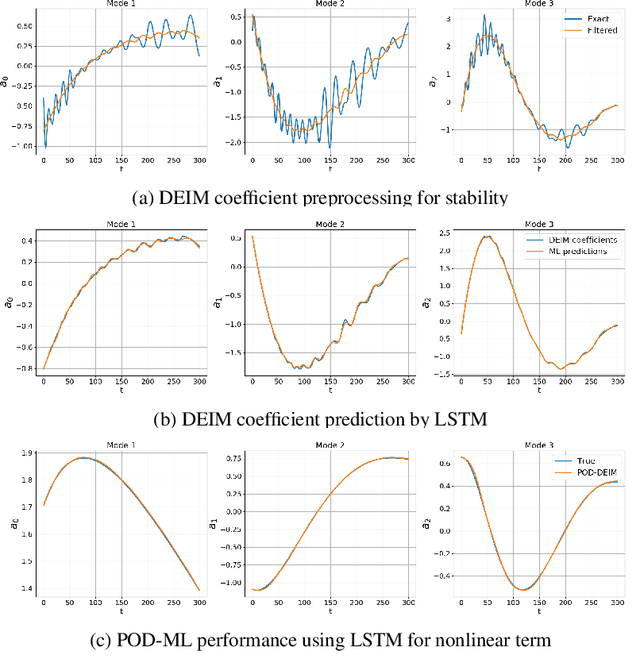
Rapid simulations of advection-dominated problems are vital for multiple engineering and geophysical applications. In this paper, we present a long short-term memory neural network to approximate the nonlinear component of the reduced-order model (ROM) of an advection-dominated partial differential equation. This is motivated by the fact that the nonlinear term is the most expensive component of a successful ROM. For our approach, we utilize a Galerkin projection to isolate the linear and the transient components of the dynamical system and then use discrete empirical interpolation to generate training data for supervised learning. We note that the numerical time-advancement and linear-term computation of the system ensure a greater preservation of physics than does a process that is fully modeled. Our results show that the proposed framework recovers transient dynamics accurately without nonlinear term computations in full-order space and represents a cost-effective alternative to solely equation-based ROMs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge