Scalable and Consistent Graph Neural Networks for Distributed Mesh-based Data-driven Modeling

This work develops a distributed graph neural network (GNN) methodology for mesh-based modeling applications using a consistent neural message passing layer. As the name implies, the focus is on enabling scalable operations that satisfy physical consistency via halo nodes at sub-graph boundaries. Here, consistency refers to the fact that a GNN trained and evaluated on one rank (one large graph) is arithmetically equivalent to evaluations on multiple ranks (a partitioned graph). This concept is demonstrated by interfacing GNNs with NekRS, a GPU-capable exascale CFD solver developed at Argonne National Laboratory. It is shown how the NekRS mesh partitioning can be linked to the distributed GNN training and inference routines, resulting in a scalable mesh-based data-driven modeling workflow. We study the impact of consistency on the scalability of mesh-based GNNs, demonstrating efficient scaling in consistent GNNs for up to O(1B) graph nodes on the Frontier exascale supercomputer.

Mesh-based Super-Resolution of Fluid Flows with Multiscale Graph Neural Networks

A graph neural network (GNN) approach is introduced in this work which enables mesh-based three-dimensional super-resolution of fluid flows. In this framework, the GNN is designed to operate not on the full mesh-based field at once, but on localized meshes of elements (or cells) directly. To facilitate mesh-based GNN representations in a manner similar to spectral (or finite) element discretizations, a baseline GNN layer (termed a message passing layer, which updates local node properties) is modified to account for synchronization of coincident graph nodes, rendering compatibility with commonly used element-based mesh connectivities. The architecture is multiscale in nature, and is comprised of a combination of coarse-scale and fine-scale message passing layer sequences (termed processors) separated by a graph unpooling layer. The coarse-scale processor embeds a query element (alongside a set number of neighboring coarse elements) into a single latent graph representation using coarse-scale synchronized message passing over the element neighborhood, and the fine-scale processor leverages additional message passing operations on this latent graph to correct for interpolation errors. Demonstration studies are performed using hexahedral mesh-based data from Taylor-Green Vortex flow simulations at Reynolds numbers of 1600 and 3200. Through analysis of both global and local errors, the results ultimately show how the GNN is able to produce accurate super-resolved fields compared to targets in both coarse-scale and multiscale model configurations. Reconstruction errors for fixed architectures were found to increase in proportion to the Reynolds number, while the inclusion of surrounding coarse element neighbors was found to improve predictions at Re=1600, but not at Re=3200.

Computationally Efficient Data-Driven Discovery and Linear Representation of Nonlinear Systems For Control

This work focuses on developing a data-driven framework using Koopman operator theory for system identification and linearization of nonlinear systems for control. Our proposed method presents a deep learning framework with recursive learning. The resulting linear system is controlled using a linear quadratic control. An illustrative example using a pendulum system is presented with simulations on noisy data. We show that our proposed method is trained more efficiently and is more accurate than an autoencoder baseline.

A Multi-Level, Multi-Scale Visual Analytics Approach to Assessment of Multifidelity HPC Systems

The ability to monitor and interpret of hardware system events and behaviors are crucial to improving the robustness and reliability of these systems, especially in a supercomputing facility. The growing complexity and scale of these systems demand an increase in monitoring data collected at multiple fidelity levels and varying temporal resolutions. In this work, we aim to build a holistic analytical system that helps make sense of such massive data, mainly the hardware logs, job logs, and environment logs collected from disparate subsystems and components of a supercomputer system. This end-to-end log analysis system, coupled with visual analytics support, allows users to glean and promptly extract supercomputer usage and error patterns at varying temporal and spatial resolutions. We use multiresolution dynamic mode decomposition (mrDMD), a technique that depicts high-dimensional data as correlated spatial-temporal variations patterns or modes, to extract variation patterns isolated at specified frequencies. Our improvements to the mrDMD algorithm help promptly reveal useful information in the massive environment log dataset, which is then associated with the processed hardware and job log datasets using our visual analytics system. Furthermore, our system can identify the usage and error patterns filtered at user, project, and subcomponent levels. We exemplify the effectiveness of our approach with two use scenarios with the Cray XC40 supercomputer.

AutoDEUQ: Automated Deep Ensemble with Uncertainty Quantification

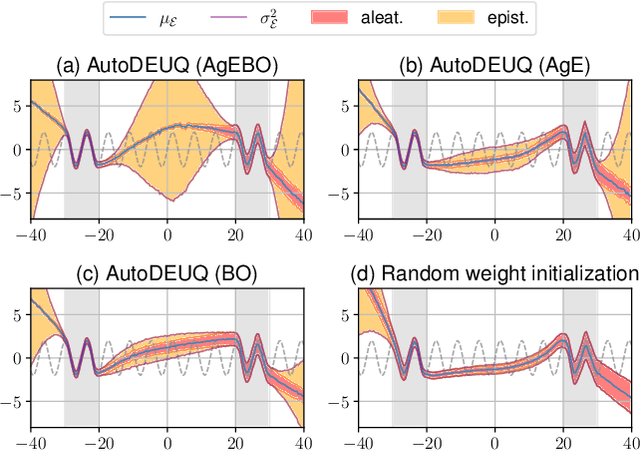
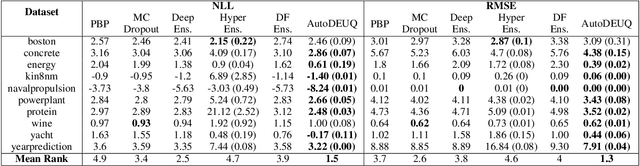
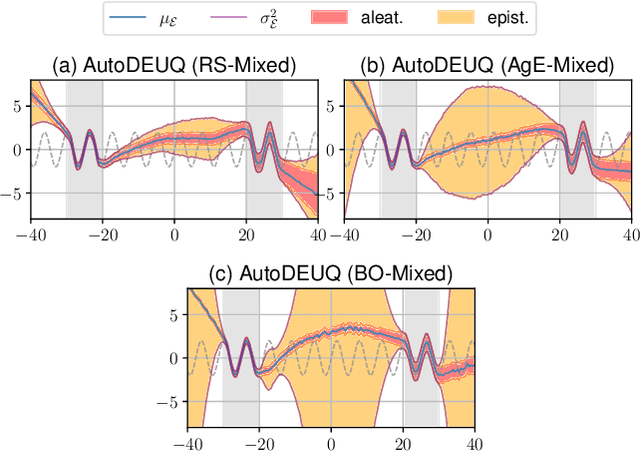
Deep neural networks are powerful predictors for a variety of tasks. However, they do not capture uncertainty directly. Using neural network ensembles to quantify uncertainty is competitive with approaches based on Bayesian neural networks while benefiting from better computational scalability. However, building ensembles of neural networks is a challenging task because, in addition to choosing the right neural architecture or hyperparameters for each member of the ensemble, there is an added cost of training each model. We propose AutoDEUQ, an automated approach for generating an ensemble of deep neural networks. Our approach leverages joint neural architecture and hyperparameter search to generate ensembles. We use the law of total variance to decompose the predictive variance of deep ensembles into aleatoric (data) and epistemic (model) uncertainties. We show that AutoDEUQ outperforms probabilistic backpropagation, Monte Carlo dropout, deep ensemble, distribution-free ensembles, and hyper ensemble methods on a number of regression benchmarks.

Deploying deep learning in OpenFOAM with TensorFlow

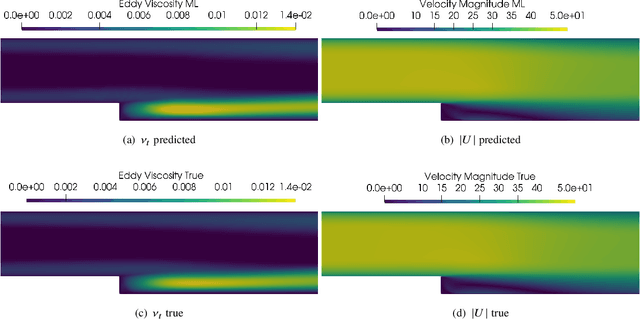
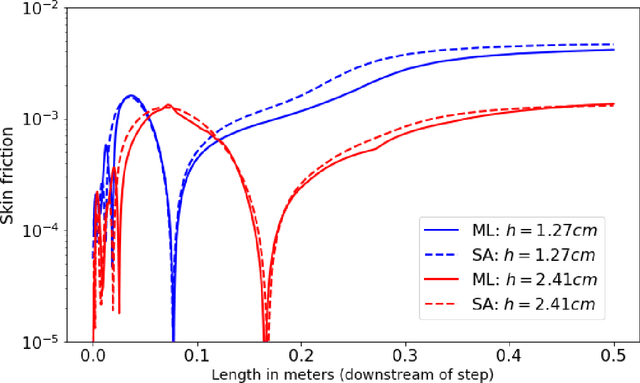
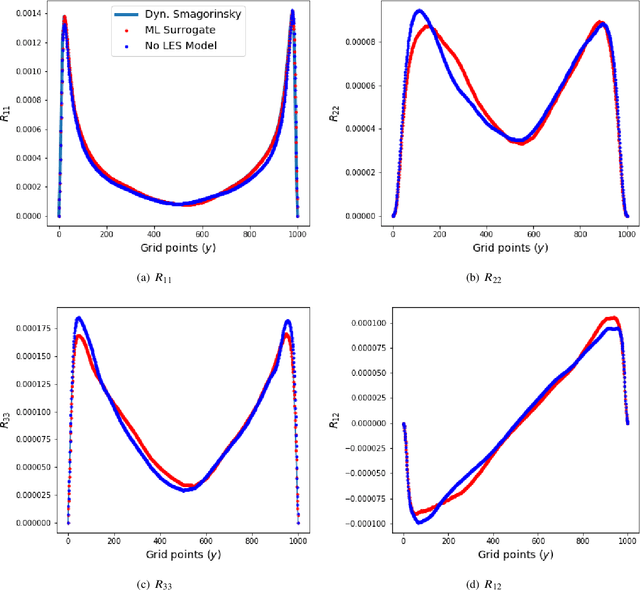
We outline the development of a data science module within OpenFOAM which allows for the in-situ deployment of trained deep learning architectures for general-purpose predictive tasks. This module is constructed with the TensorFlow C API and is integrated into OpenFOAM as an application that may be linked at run time. Notably, our formulation precludes any restrictions related to the type of neural network architecture (i.e., convolutional, fully-connected, etc.). This allows for potential studies of complicated neural architectures for practical CFD problems. In addition, the proposed module outlines a path towards an open-source, unified and transparent framework for computational fluid dynamics and machine learning.

Deep Learning Models for Global Coordinate Transformations that Linearize PDEs

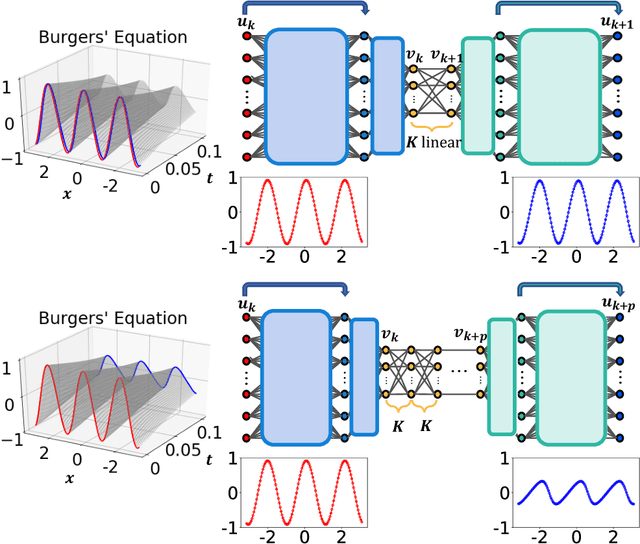
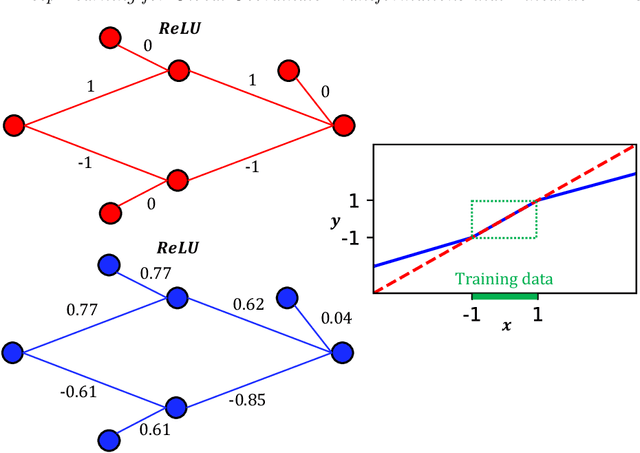
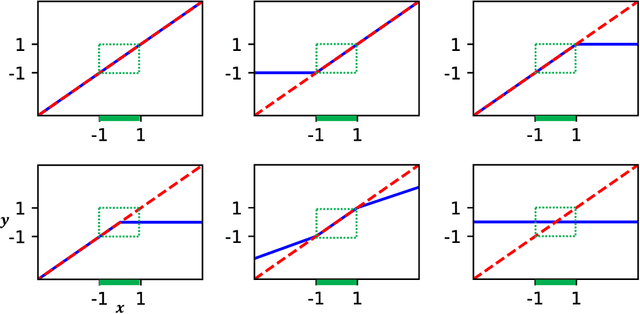
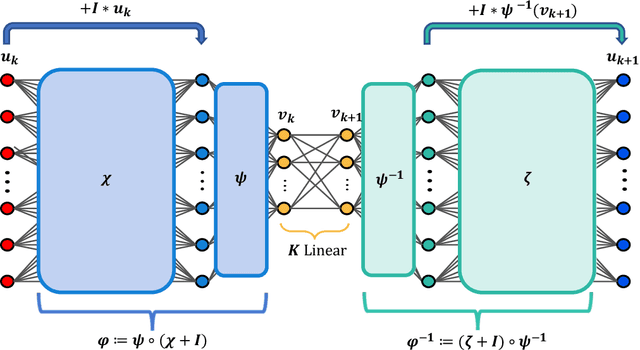
We develop a deep autoencoder architecture that can be used to find a coordinate transformation which turns a nonlinear PDE into a linear PDE. Our architecture is motivated by the linearizing transformations provided by the Cole-Hopf transform for Burgers equation and the inverse scattering transform for completely integrable PDEs. By leveraging a residual network architecture, a near-identity transformation can be exploited to encode intrinsic coordinates in which the dynamics are linear. The resulting dynamics are given by a Koopman operator matrix $\mathbf{K}$. The decoder allows us to transform back to the original coordinates as well. Multiple time step prediction can be performed by repeated multiplication by the matrix $\mathbf{K}$ in the intrinsic coordinates. We demonstrate our method on a number of examples, including the heat equation and Burgers equation, as well as the substantially more challenging Kuramoto-Sivashinsky equation, showing that our method provides a robust architecture for discovering interpretable, linearizing transforms for nonlinear PDEs.

Using recurrent neural networks for nonlinear component computation in advection-dominated reduced-order models

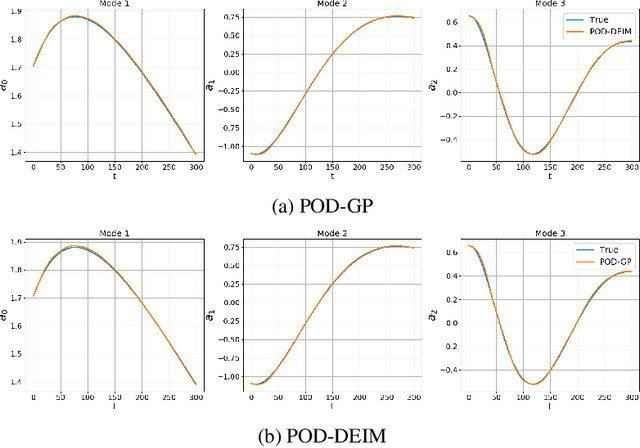
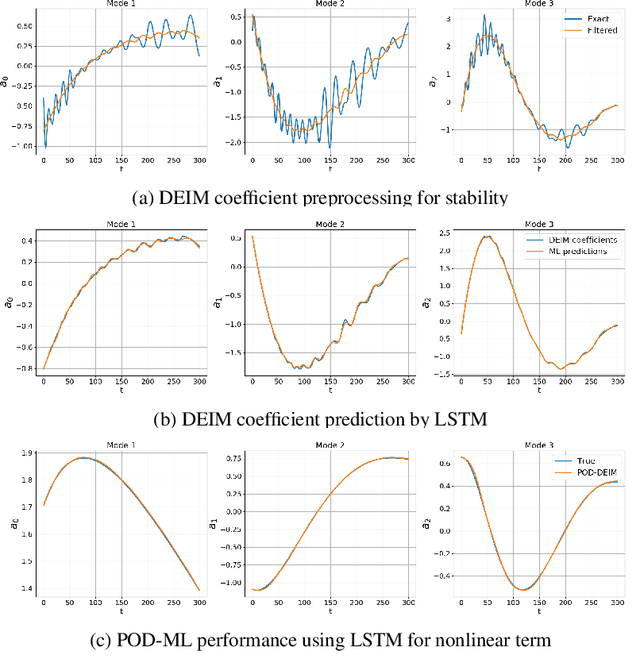
Rapid simulations of advection-dominated problems are vital for multiple engineering and geophysical applications. In this paper, we present a long short-term memory neural network to approximate the nonlinear component of the reduced-order model (ROM) of an advection-dominated partial differential equation. This is motivated by the fact that the nonlinear term is the most expensive component of a successful ROM. For our approach, we utilize a Galerkin projection to isolate the linear and the transient components of the dynamical system and then use discrete empirical interpolation to generate training data for supervised learning. We note that the numerical time-advancement and linear-term computation of the system ensure a greater preservation of physics than does a process that is fully modeled. Our results show that the proposed framework recovers transient dynamics accurately without nonlinear term computations in full-order space and represents a cost-effective alternative to solely equation-based ROMs.

Deep learning for universal linear embeddings of nonlinear dynamics

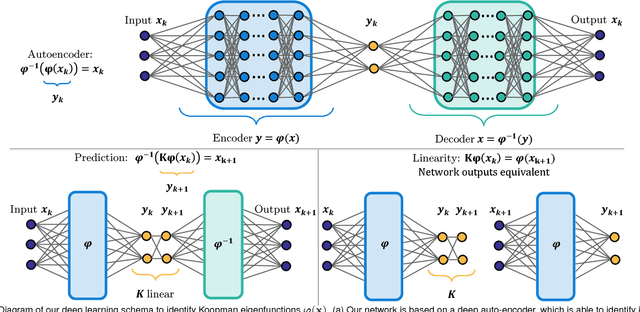
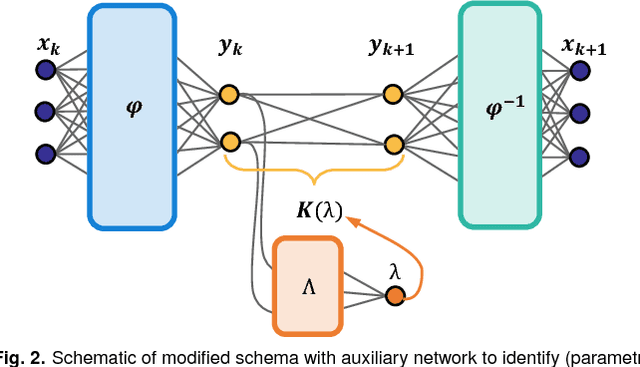
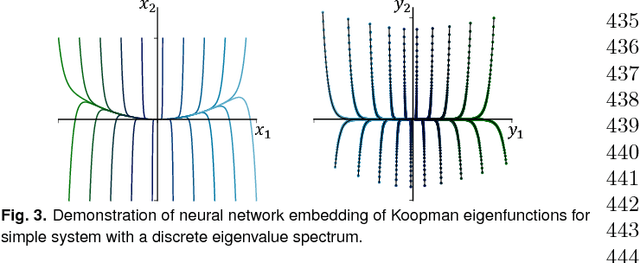
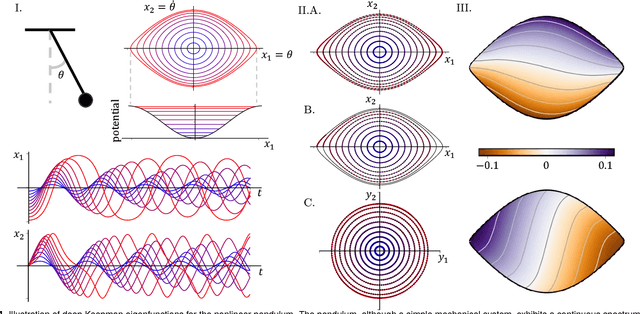
Identifying coordinate transformations that make strongly nonlinear dynamics approximately linear is a central challenge in modern dynamical systems. These transformations have the potential to enable prediction, estimation, and control of nonlinear systems using standard linear theory. The Koopman operator has emerged as a leading data-driven embedding, as eigenfunctions of this operator provide intrinsic coordinates that globally linearize the dynamics. However, identifying and representing these eigenfunctions has proven to be mathematically and computationally challenging. This work leverages the power of deep learning to discover representations of Koopman eigenfunctions from trajectory data of dynamical systems. Our network is parsimonious and interpretable by construction, embedding the dynamics on a low-dimensional manifold that is of the intrinsic rank of the dynamics and parameterized by the Koopman eigenfunctions. In particular, we identify nonlinear coordinates on which the dynamics are globally linear using a modified auto-encoder. We also generalize Koopman representations to include a ubiquitous class of systems that exhibit continuous spectra, ranging from the simple pendulum to nonlinear optics and broadband turbulence. Our framework parametrizes the continuous frequency using an auxiliary network, enabling a compact and efficient embedding at the intrinsic rank, while connecting our models to half a century of asymptotics. In this way, we benefit from the power and generality of deep learning, while retaining the physical interpretability of Koopman embeddings.

Modeling cognitive deficits following neurodegenerative diseases and traumatic brain injuries with deep convolutional neural networks

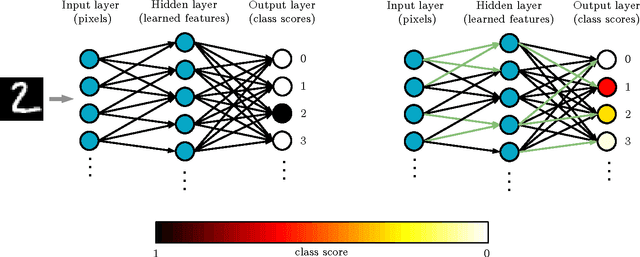
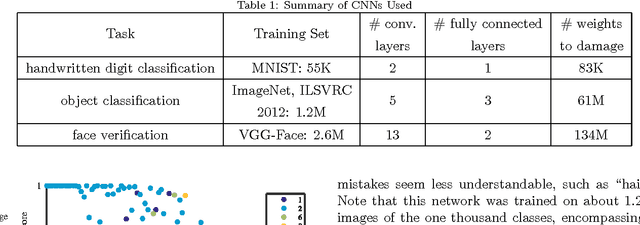
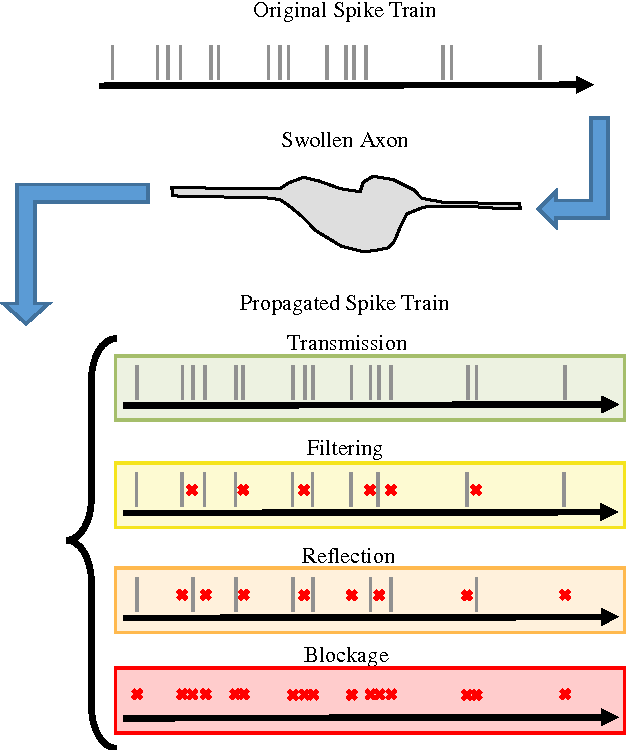
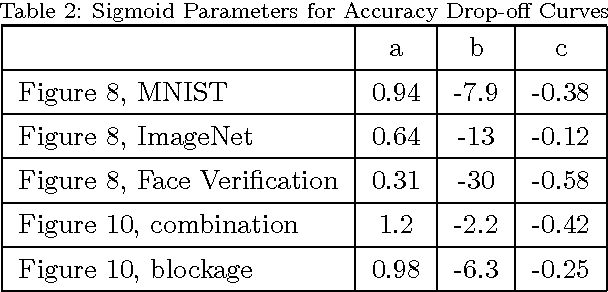
The accurate diagnosis and assessment of neurodegenerative disease and traumatic brain injuries (TBI) remain open challenges. Both cause cognitive and functional deficits due to focal axonal swellings (FAS), but it is difficult to deliver a prognosis due to our limited ability to assess damaged neurons at a cellular level in vivo. We simulate the effects of neurodegenerative disease and TBI using convolutional neural networks (CNNs) as our model of cognition. We utilize biophysically relevant statistical data on FAS to damage the connections in CNNs in a functionally relevant way. We incorporate energy constraints on the brain by pruning the CNNs to be less over-engineered. Qualitatively, we demonstrate that damage leads to human-like mistakes. Our experiments also provide quantitative assessments of how accuracy is affected by various types and levels of damage. The deficit resulting from a fixed amount of damage greatly depends on which connections are randomly injured, providing intuition for why it is difficult to predict impairments. There is a large degree of subjectivity when it comes to interpreting cognitive deficits from complex systems such as the human brain. However, we provide important insight and a quantitative framework for disorders in which FAS are implicated.