Scalable and Consistent Graph Neural Networks for Distributed Mesh-based Data-driven Modeling

This work develops a distributed graph neural network (GNN) methodology for mesh-based modeling applications using a consistent neural message passing layer. As the name implies, the focus is on enabling scalable operations that satisfy physical consistency via halo nodes at sub-graph boundaries. Here, consistency refers to the fact that a GNN trained and evaluated on one rank (one large graph) is arithmetically equivalent to evaluations on multiple ranks (a partitioned graph). This concept is demonstrated by interfacing GNNs with NekRS, a GPU-capable exascale CFD solver developed at Argonne National Laboratory. It is shown how the NekRS mesh partitioning can be linked to the distributed GNN training and inference routines, resulting in a scalable mesh-based data-driven modeling workflow. We study the impact of consistency on the scalability of mesh-based GNNs, demonstrating efficient scaling in consistent GNNs for up to O(1B) graph nodes on the Frontier exascale supercomputer.

Mesh-based Super-Resolution of Fluid Flows with Multiscale Graph Neural Networks

A graph neural network (GNN) approach is introduced in this work which enables mesh-based three-dimensional super-resolution of fluid flows. In this framework, the GNN is designed to operate not on the full mesh-based field at once, but on localized meshes of elements (or cells) directly. To facilitate mesh-based GNN representations in a manner similar to spectral (or finite) element discretizations, a baseline GNN layer (termed a message passing layer, which updates local node properties) is modified to account for synchronization of coincident graph nodes, rendering compatibility with commonly used element-based mesh connectivities. The architecture is multiscale in nature, and is comprised of a combination of coarse-scale and fine-scale message passing layer sequences (termed processors) separated by a graph unpooling layer. The coarse-scale processor embeds a query element (alongside a set number of neighboring coarse elements) into a single latent graph representation using coarse-scale synchronized message passing over the element neighborhood, and the fine-scale processor leverages additional message passing operations on this latent graph to correct for interpolation errors. Demonstration studies are performed using hexahedral mesh-based data from Taylor-Green Vortex flow simulations at Reynolds numbers of 1600 and 3200. Through analysis of both global and local errors, the results ultimately show how the GNN is able to produce accurate super-resolved fields compared to targets in both coarse-scale and multiscale model configurations. Reconstruction errors for fixed architectures were found to increase in proportion to the Reynolds number, while the inclusion of surrounding coarse element neighbors was found to improve predictions at Re=1600, but not at Re=3200.

Differentiable physics-enabled closure modeling for Burgers' turbulence

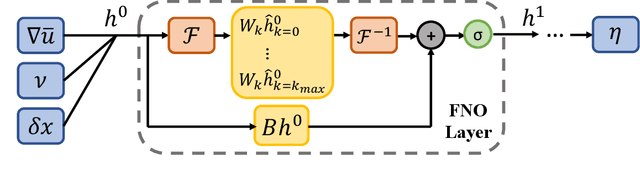
Data-driven turbulence modeling is experiencing a surge in interest following algorithmic and hardware developments in the data sciences. We discuss an approach using the differentiable physics paradigm that combines known physics with machine learning to develop closure models for Burgers' turbulence. We consider the 1D Burgers system as a prototypical test problem for modeling the unresolved terms in advection-dominated turbulence problems. We train a series of models that incorporate varying degrees of physical assumptions on an a posteriori loss function to test the efficacy of models across a range of system parameters, including viscosity, time, and grid resolution. We find that constraining models with inductive biases in the form of partial differential equations that contain known physics or existing closure approaches produces highly data-efficient, accurate, and generalizable models, outperforming state-of-the-art baselines. Addition of structure in the form of physics information also brings a level of interpretability to the models, potentially offering a stepping stone to the future of closure modeling.