FIGNN: Feature-Specific Interpretability for Graph Neural Network Surrogate Models

This work presents a novel graph neural network (GNN) architecture, the Feature-specific Interpretable Graph Neural Network (FIGNN), designed to enhance the interpretability of deep learning surrogate models defined on unstructured grids in scientific applications. Traditional GNNs often obscure the distinct spatial influences of different features in multivariate prediction tasks. FIGNN addresses this limitation by introducing a feature-specific pooling strategy, which enables independent attribution of spatial importance for each predicted variable. Additionally, a mask-based regularization term is incorporated into the training objective to explicitly encourage alignment between interpretability and predictive error, promoting localized attribution of model performance. The method is evaluated for surrogate modeling of two physically distinct systems: the SPEEDY atmospheric circulation model and the backward-facing step (BFS) fluid dynamics benchmark. Results demonstrate that FIGNN achieves competitive predictive performance while revealing physically meaningful spatial patterns unique to each feature. Analysis of rollout stability, feature-wise error budgets, and spatial mask overlays confirm the utility of FIGNN as a general-purpose framework for interpretable surrogate modeling in complex physical domains.

Scalable and Consistent Graph Neural Networks for Distributed Mesh-based Data-driven Modeling

This work develops a distributed graph neural network (GNN) methodology for mesh-based modeling applications using a consistent neural message passing layer. As the name implies, the focus is on enabling scalable operations that satisfy physical consistency via halo nodes at sub-graph boundaries. Here, consistency refers to the fact that a GNN trained and evaluated on one rank (one large graph) is arithmetically equivalent to evaluations on multiple ranks (a partitioned graph). This concept is demonstrated by interfacing GNNs with NekRS, a GPU-capable exascale CFD solver developed at Argonne National Laboratory. It is shown how the NekRS mesh partitioning can be linked to the distributed GNN training and inference routines, resulting in a scalable mesh-based data-driven modeling workflow. We study the impact of consistency on the scalability of mesh-based GNNs, demonstrating efficient scaling in consistent GNNs for up to O(1B) graph nodes on the Frontier exascale supercomputer.

Mesh-based Super-Resolution of Fluid Flows with Multiscale Graph Neural Networks

A graph neural network (GNN) approach is introduced in this work which enables mesh-based three-dimensional super-resolution of fluid flows. In this framework, the GNN is designed to operate not on the full mesh-based field at once, but on localized meshes of elements (or cells) directly. To facilitate mesh-based GNN representations in a manner similar to spectral (or finite) element discretizations, a baseline GNN layer (termed a message passing layer, which updates local node properties) is modified to account for synchronization of coincident graph nodes, rendering compatibility with commonly used element-based mesh connectivities. The architecture is multiscale in nature, and is comprised of a combination of coarse-scale and fine-scale message passing layer sequences (termed processors) separated by a graph unpooling layer. The coarse-scale processor embeds a query element (alongside a set number of neighboring coarse elements) into a single latent graph representation using coarse-scale synchronized message passing over the element neighborhood, and the fine-scale processor leverages additional message passing operations on this latent graph to correct for interpolation errors. Demonstration studies are performed using hexahedral mesh-based data from Taylor-Green Vortex flow simulations at Reynolds numbers of 1600 and 3200. Through analysis of both global and local errors, the results ultimately show how the GNN is able to produce accurate super-resolved fields compared to targets in both coarse-scale and multiscale model configurations. Reconstruction errors for fixed architectures were found to increase in proportion to the Reynolds number, while the inclusion of surrounding coarse element neighbors was found to improve predictions at Re=1600, but not at Re=3200.

A note on the error analysis of data-driven closure models for large eddy simulations of turbulence

In this work, we provide a mathematical formulation for error propagation in flow trajectory prediction using data-driven turbulence closure modeling. Under the assumption that the predicted state of a large eddy simulation prediction must be close to that of a subsampled direct numerical simulation, we retrieve an upper bound for the prediction error when utilizing a data-driven closure model. We also demonstrate that this error is significantly affected by the time step size and the Jacobian which play a role in amplifying the initial one-step error made by using the closure. Our analysis also shows that the error propagates exponentially with rollout time and the upper bound of the system Jacobian which is itself influenced by the Jacobian of the closure formulation. These findings could enable the development of new regularization techniques for ML models based on the identified error-bound terms, improving their robustness and reducing error propagation.

Interpretable Fine-Tuning for Graph Neural Network Surrogate Models

Data-based surrogate modeling has surged in capability in recent years with the emergence of graph neural networks (GNNs), which can operate directly on mesh-based representations of data. The goal of this work is to introduce an interpretable fine-tuning strategy for GNNs, with application to unstructured mesh-based fluid dynamics modeling. The end result is a fine-tuned GNN that adds interpretability to a pre-trained baseline GNN through an adaptive sub-graph sampling strategy that isolates regions in physical space intrinsically linked to the forecasting task, while retaining the predictive capability of the baseline. The structures identified by the fine-tuned GNNs, which are adaptively produced in the forward pass as explicit functions of the input, serve as an accessible link between the baseline model architecture, the optimization goal, and known problem-specific physics. Additionally, through a regularization procedure, the fine-tuned GNNs can also be used to identify, during inference, graph nodes that correspond to a majority of the anticipated forecasting error, adding a novel interpretable error-tagging capability to baseline models. Demonstrations are performed using unstructured flow data sourced from flow over a backward-facing step at high Reynolds numbers.

Jacobian-Scaled K-means Clustering for Physics-Informed Segmentation of Reacting Flows

This work introduces Jacobian-scaled K-means (JSK-means) clustering, which is a physics-informed clustering strategy centered on the K-means framework. The method allows for the injection of underlying physical knowledge into the clustering procedure through a distance function modification: instead of leveraging conventional Euclidean distance vectors, the JSK-means procedure operates on distance vectors scaled by matrices obtained from dynamical system Jacobians evaluated at the cluster centroids. The goal of this work is to show how the JSK-means algorithm -- without modifying the input dataset -- produces clusters that capture regions of dynamical similarity, in that the clusters are redistributed towards high-sensitivity regions in phase space and are described by similarity in the source terms of samples instead of the samples themselves. The algorithm is demonstrated on a complex reacting flow simulation dataset (a channel detonation configuration), where the dynamics in the thermochemical composition space are known through the highly nonlinear and stiff Arrhenius-based chemical source terms. Interpretations of cluster partitions in both physical space and composition space reveal how JSK-means shifts clusters produced by standard K-means towards regions of high chemical sensitivity (e.g., towards regions of peak heat release rate near the detonation reaction zone). The findings presented here illustrate the benefits of utilizing Jacobian-scaled distances in clustering techniques, and the JSK-means method in particular displays promising potential for improving former partition-based modeling strategies in reacting flow (and other multi-physics) applications.

Multiscale Graph Neural Network Autoencoders for Interpretable Scientific Machine Learning

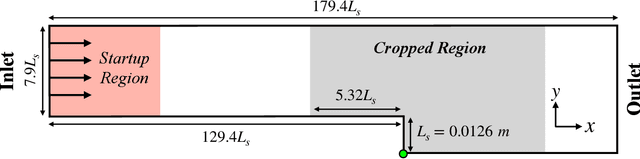
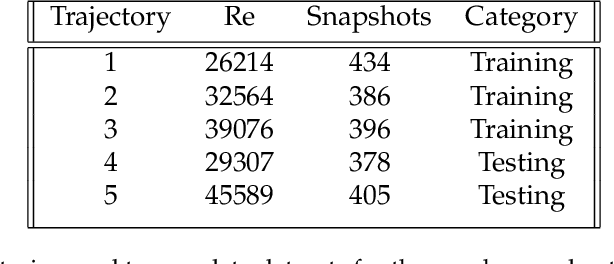
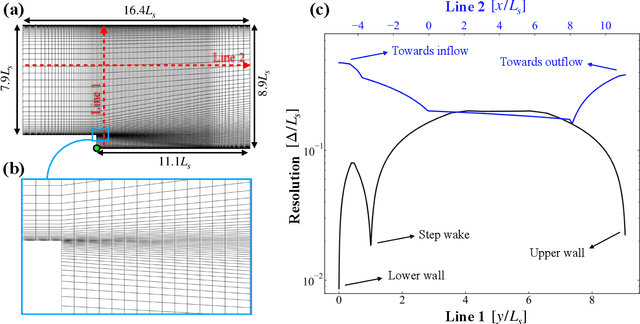
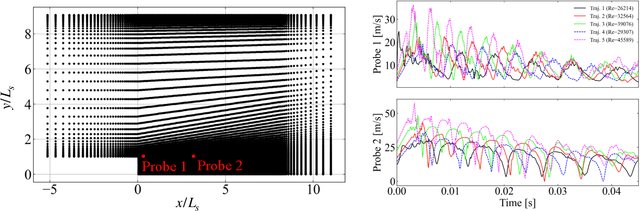
The goal of this work is to address two limitations in autoencoder-based models: latent space interpretability and compatibility with unstructured meshes. This is accomplished here with the development of a novel graph neural network (GNN) autoencoding architecture with demonstrations on complex fluid flow applications. To address the first goal of interpretability, the GNN autoencoder achieves reduction in the number nodes in the encoding stage through an adaptive graph reduction procedure. This reduction procedure essentially amounts to flowfield-conditioned node sampling and sensor identification, and produces interpretable latent graph representations tailored to the flowfield reconstruction task in the form of so-called masked fields. These masked fields allow the user to (a) visualize where in physical space a given latent graph is active, and (b) interpret the time-evolution of the latent graph connectivity in accordance with the time-evolution of unsteady flow features (e.g. recirculation zones, shear layers) in the domain. To address the goal of unstructured mesh compatibility, the autoencoding architecture utilizes a series of multi-scale message passing (MMP) layers, each of which models information exchange among node neighborhoods at various lengthscales. The MMP layer, which augments standard single-scale message passing with learnable coarsening operations, allows the decoder to more efficiently reconstruct the flowfield from the identified regions in the masked fields. Analysis of latent graphs produced by the autoencoder for various model settings are conducted using using unstructured snapshot data sourced from large-eddy simulations in a backward-facing step (BFS) flow configuration with an OpenFOAM-based flow solver at high Reynolds numbers.

Using machine learning to construct velocity fields from OH-PLIF images

This work utilizes data-driven methods to morph a series of time-resolved experimental OH-PLIF images into corresponding three-component planar PIV fields in the closed domain of a premixed swirl combustor. The task is carried out with a fully convolutional network, which is a type of convolutional neural network (CNN) used in many applications in machine learning, alongside an existing experimental dataset which consists of simultaneous OH-PLIF and PIV measurements in both attached and detached flame regimes. Two types of models are compared: 1) a global CNN which is trained using images from the entire domain, and 2) a set of local CNNs, which are trained only on individual sections of the domain. The locally trained models show improvement in creating mappings in the detached regime over the global models. A comparison between model performance in attached and detached regimes shows that the CNNs are much more accurate across the board in creating velocity fields for attached flames. Inclusion of time history in the PLIF input resulted in small noticeable improvement on average, which could imply a greater physical role of instantaneous spatial correlations in the decoding process over temporal dependencies from the perspective of the CNN. Additionally, the performance of local models trained to produce mappings in one section of the domain is tested on other, unexplored sections of the domain. Interestingly, local CNN performance on unseen domain regions revealed the models' ability to utilize symmetry and antisymmetry in the velocity field. Ultimately, this work shows the powerful ability of the CNN to decode the three-dimensional PIV fields from input OH-PLIF images, providing a potential groundwork for a very useful tool for experimental configurations in which accessibility of forms of simultaneous measurements are limited.