Learning second-order TVD flux limiters using differentiable solvers

This paper presents a data-driven framework for learning optimal second-order total variation diminishing (TVD) flux limiters via differentiable simulations. In our fully differentiable finite volume solvers, the limiter functions are replaced by neural networks. By representing the limiter as a pointwise convex linear combination of the Minmod and Superbee limiters, we enforce both second-order accuracy and TVD constraints at all stages of training. Our approach leverages gradient-based optimization through automatic differentiation, allowing a direct backpropagation of errors from numerical solutions to the limiter parameters. We demonstrate the effectiveness of this method on various hyperbolic conservation laws, including the linear advection equation, the Burgers' equation, and the one-dimensional Euler equations. Remarkably, a limiter trained solely on linear advection exhibits strong generalizability, surpassing the accuracy of most classical flux limiters across a range of problems with shocks and discontinuities. The learned flux limiters can be readily integrated into existing computational fluid dynamics codes, and the proposed methodology also offers a flexible pathway to systematically develop and optimize flux limiters for complex flow problems.

Self-supervised Pretraining for Partial Differential Equations

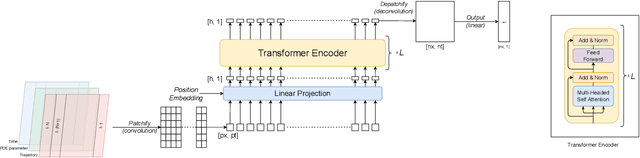
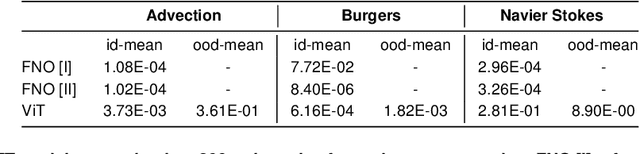
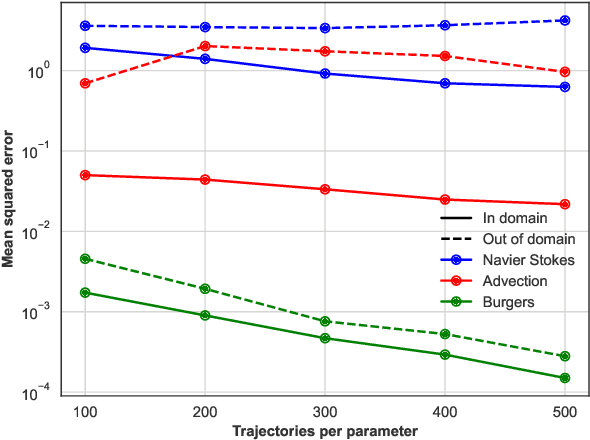
In this work, we describe a novel approach to building a neural PDE solver leveraging recent advances in transformer based neural network architectures. Our model can provide solutions for different values of PDE parameters without any need for retraining the network. The training is carried out in a self-supervised manner, similar to pretraining approaches applied in language and vision tasks. We hypothesize that the model is in effect learning a family of operators (for multiple parameters) mapping the initial condition to the solution of the PDE at any future time step t. We compare this approach with the Fourier Neural Operator (FNO), and demonstrate that it can generalize over the space of PDE parameters, despite having a higher prediction error for individual parameter values compared to the FNO. We show that performance on a specific parameter can be improved by finetuning the model with very small amounts of data. We also demonstrate that the model scales with data as well as model size.

Differentiable Chemical Physics by Geometric Deep Learning for Gradient-based Property Optimization of Mixtures

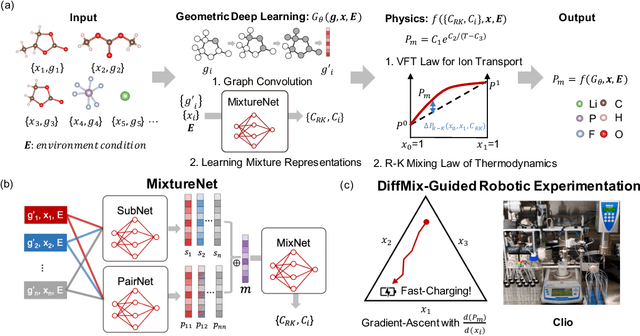
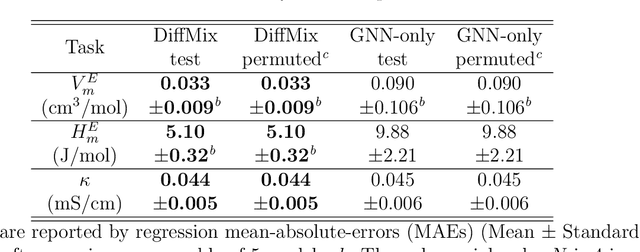
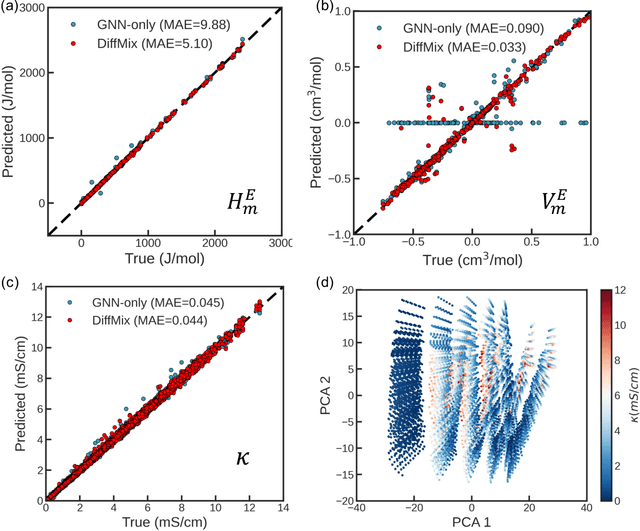
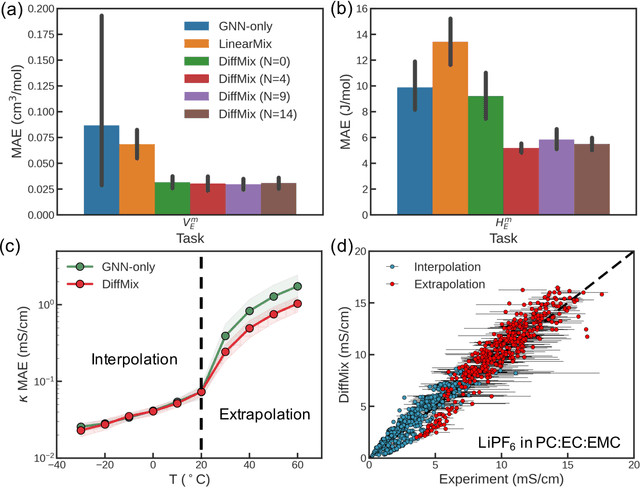
Chemical mixtures, satisfying multi-objective performance metrics and constraints, enable their use in chemical processes and electrochemical devices. In this work, we develop a differentiable chemical-physics framework for modeling chemical mixtures, DiffMix, where geometric deep learning (GDL) is leveraged to map from molecular species, compositions and environment conditions, to physical coefficients in the mixture physics laws. In particular, we extend mixture thermodynamic and transport laws by creating learnable physical coefficients, where we use graph neural networks as the molecule encoder and enforce component-wise permutation-invariance. We start our model evaluations with thermodynamics of binary mixtures, and further benchmarked multicomponent electrolyte mixtures on their transport properties, in order to test the model generalizability. We show improved prediction accuracy and model robustness of DiffMix than its purely data-driven variants. Furthermore, we demonstrate the efficient optimization of electrolyte transport properties, built on the gradient obtained using DiffMix auto-differentiation. Our simulation runs are then backed up by the data generated by a robotic experimentation setup, Clio. By combining mixture physics and GDL, DiffMix expands the predictive modeling methods for chemical mixtures and provides low-cost optimization approaches in large chemical spaces.

Differentiable Turbulence II

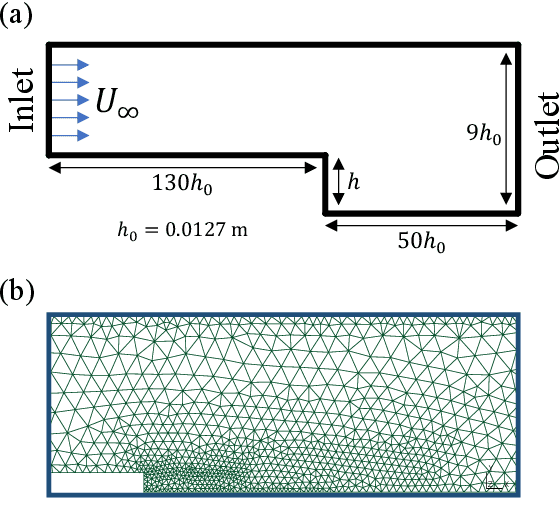
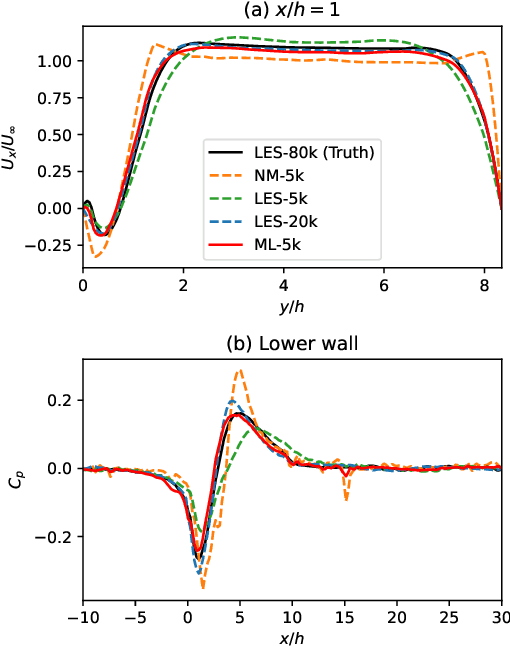
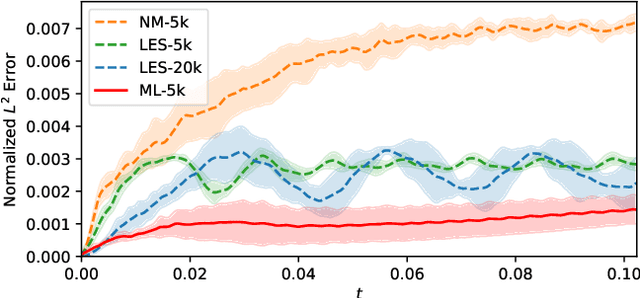
Differentiable fluid simulators are increasingly demonstrating value as useful tools for developing data-driven models in computational fluid dynamics (CFD). Differentiable turbulence, or the end-to-end training of machine learning (ML) models embedded in CFD solution algorithms, captures both the generalization power and limited upfront cost of physics-based simulations, and the flexibility and automated training of deep learning methods. We develop a framework for integrating deep learning models into a generic finite element numerical scheme for solving the Navier-Stokes equations, applying the technique to learn a sub-grid scale closure using a multi-scale graph neural network. We demonstrate the method on several realizations of flow over a backwards-facing step, testing on both unseen Reynolds numbers and new geometry. We show that the learned closure can achieve accuracy comparable to traditional large eddy simulation on a finer grid that amounts to an equivalent speedup of 10x. As the desire and need for cheaper CFD simulations grows, we see hybrid physics-ML methods as a path forward to be exploited in the near future.

Differentiable Turbulence

Deep learning is increasingly becoming a promising pathway to improving the accuracy of sub-grid scale (SGS) turbulence closure models for large eddy simulations (LES). We leverage the concept of differentiable turbulence, whereby an end-to-end differentiable solver is used in combination with physics-inspired choices of deep learning architectures to learn highly effective and versatile SGS models for two-dimensional turbulent flow. We perform an in-depth analysis of the inductive biases in the chosen architectures, finding that the inclusion of small-scale non-local features is most critical to effective SGS modeling, while large-scale features can improve pointwise accuracy of the a-posteriori solution field. The filtered velocity gradient tensor can be mapped directly to the SGS stress via decomposition of the inputs and outputs into isotropic, deviatoric, and anti-symmetric components. We see that the model can generalize to a variety of flow configurations, including higher and lower Reynolds numbers and different forcing conditions. We show that the differentiable physics paradigm is more successful than offline, a-priori learning, and that hybrid solver-in-the-loop approaches to deep learning offer an ideal balance between computational efficiency, accuracy, and generalization. Our experiments provide physics-based recommendations for deep-learning based SGS modeling for generalizable closure modeling of turbulence.

Chemellia: An Ecosystem for Atomistic Scientific Machine Learning

Chemellia is an open-source framework for atomistic machine learning in the Julia programming language. The framework takes advantage of Julia's high speed as well as the ability to share and reuse code and interfaces through the paradigm of multiple dispatch. Chemellia is designed to make use of existing interfaces and avoid ``reinventing the wheel'' wherever possible. A key aspect of the Chemellia ecosystem is the ChemistryFeaturization interface for defining and encoding features -- it is designed to maximize interoperability between featurization schemes and elements thereof, to maintain provenance of encoded features, and to ensure easy decodability and reconfigurability to enable feature engineering experiments. This embodies the overall design principles of the Chemellia ecosystem: separation of concerns, interoperability, and transparency. We illustrate these principles by discussing the implementation of crystal graph convolutional neural networks for material property prediction.

Multiscale Graph Neural Network Autoencoders for Interpretable Scientific Machine Learning

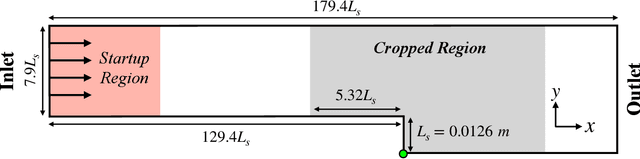
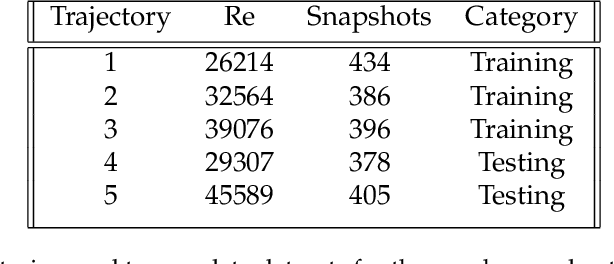
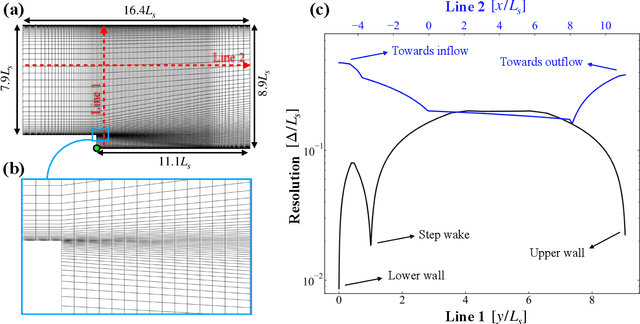
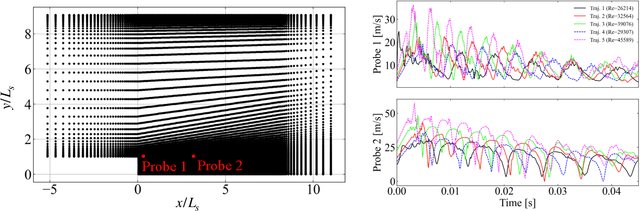
The goal of this work is to address two limitations in autoencoder-based models: latent space interpretability and compatibility with unstructured meshes. This is accomplished here with the development of a novel graph neural network (GNN) autoencoding architecture with demonstrations on complex fluid flow applications. To address the first goal of interpretability, the GNN autoencoder achieves reduction in the number nodes in the encoding stage through an adaptive graph reduction procedure. This reduction procedure essentially amounts to flowfield-conditioned node sampling and sensor identification, and produces interpretable latent graph representations tailored to the flowfield reconstruction task in the form of so-called masked fields. These masked fields allow the user to (a) visualize where in physical space a given latent graph is active, and (b) interpret the time-evolution of the latent graph connectivity in accordance with the time-evolution of unsteady flow features (e.g. recirculation zones, shear layers) in the domain. To address the goal of unstructured mesh compatibility, the autoencoding architecture utilizes a series of multi-scale message passing (MMP) layers, each of which models information exchange among node neighborhoods at various lengthscales. The MMP layer, which augments standard single-scale message passing with learnable coarsening operations, allows the decoder to more efficiently reconstruct the flowfield from the identified regions in the masked fields. Analysis of latent graphs produced by the autoencoder for various model settings are conducted using using unstructured snapshot data sourced from large-eddy simulations in a backward-facing step (BFS) flow configuration with an OpenFOAM-based flow solver at high Reynolds numbers.

Differentiable physics-enabled closure modeling for Burgers' turbulence

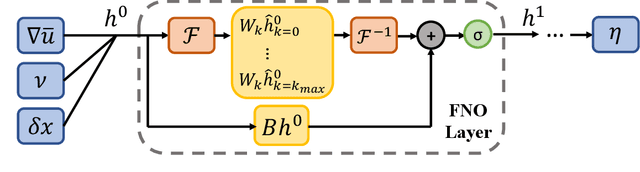
Data-driven turbulence modeling is experiencing a surge in interest following algorithmic and hardware developments in the data sciences. We discuss an approach using the differentiable physics paradigm that combines known physics with machine learning to develop closure models for Burgers' turbulence. We consider the 1D Burgers system as a prototypical test problem for modeling the unresolved terms in advection-dominated turbulence problems. We train a series of models that incorporate varying degrees of physical assumptions on an a posteriori loss function to test the efficacy of models across a range of system parameters, including viscosity, time, and grid resolution. We find that constraining models with inductive biases in the form of partial differential equations that contain known physics or existing closure approaches produces highly data-efficient, accurate, and generalizable models, outperforming state-of-the-art baselines. Addition of structure in the form of physics information also brings a level of interpretability to the models, potentially offering a stepping stone to the future of closure modeling.

Score-Based Generative Models for Molecule Generation

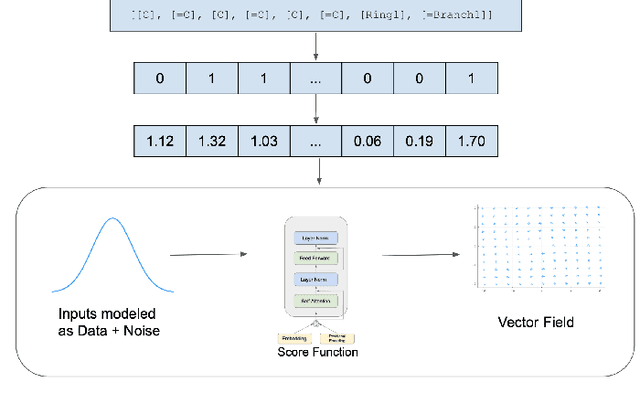
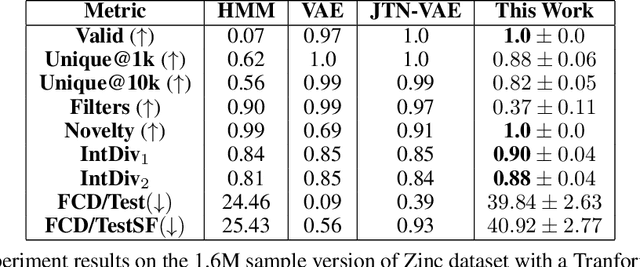
Recent advances in generative models have made exploring design spaces easier for de novo molecule generation. However, popular generative models like GANs and normalizing flows face challenges such as training instabilities due to adversarial training and architectural constraints, respectively. Score-based generative models sidestep these challenges by modelling the gradient of the log probability density using a score function approximation, as opposed to modelling the density function directly, and sampling from it using annealed Langevin Dynamics. We believe that score-based generative models could open up new opportunities in molecule generation due to their architectural flexibility, such as replacing the score function with an SE(3) equivariant model. In this work, we lay the foundations by testing the efficacy of score-based models for molecule generation. We train a Transformer-based score function on Self-Referencing Embedded Strings (SELFIES) representations of 1.5 million samples from the ZINC dataset and use the Moses benchmarking framework to evaluate the generated samples on a suite of metrics.

Autonomous optimization of nonaqueous battery electrolytes via robotic experimentation and machine learning

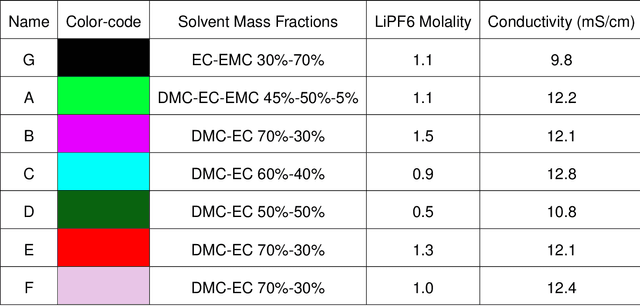
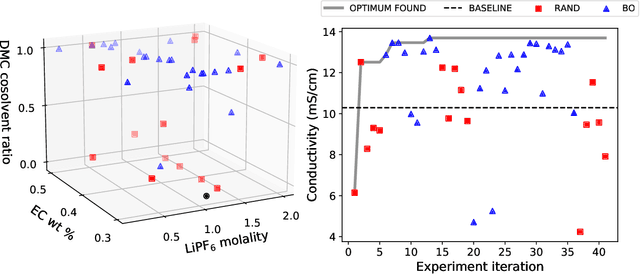
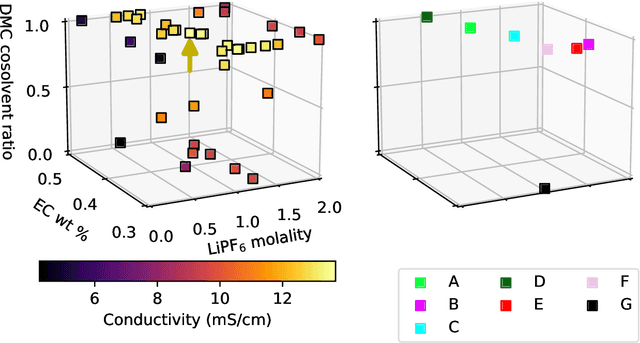
In this work, we introduce a novel workflow that couples robotics to machine-learning for efficient optimization of a non-aqueous battery electrolyte. A custom-built automated experiment named "Clio" is coupled to Dragonfly - a Bayesian optimization-based experiment planner. Clio autonomously optimizes electrolyte conductivity over a single-salt, ternary solvent design space. Using this workflow, we identify 6 fast-charging electrolytes in 2 work-days and 42 experiments (compared with 60 days using exhaustive search of the 1000 possible candidates, or 6 days assuming only 10% of candidates are evaluated). Our method finds the highest reported conductivity electrolyte in a design space heavily explored by previous literature, converging on a high-conductivity mixture that demonstrates subtle electrolyte chemical physics.